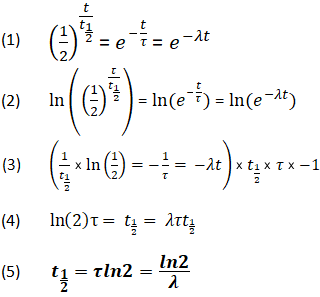Las siguientes herramientas pueden generar cualquiera de los valores de los otros tres en la fórmula de vida media para que una sustancia que sufre decaimiento disminuya a la mitad.

Calculadora de vida media
Por favor, proporcione cualquiera de los tres siguientes para calcular el cuarto valor.
Conversión de Vida Media, Vida Media y Constante de Decaimiento
Por favor, proporcione cualquiera de los siguientes para obtener los otros dos.
Definición y Fórmula
La vida media se define como la cantidad de tiempo que tarda una cantidad dada en disminuir a la mitad de su valor inicial. El término se utiliza más comúnmente en relación con los átomos que sufren desintegración radiactiva, pero puede utilizarse para describir otros tipos de desintegración, ya sea exponencial o no. Una de las aplicaciones más conocidas de la vida media es la datación por carbono-14. La vida media del carbono-14 es de aproximadamente 5.730 años, y puede utilizarse de forma fiable para medir fechas hasta hace unos 50.000 años. El proceso de datación por carbono-14 fue desarrollado por William Libby, y se basa en el hecho de que el carbono-14 se produce constantemente en la atmósfera. Se incorpora a las plantas a través de la fotosíntesis, y luego a los animales cuando consumen plantas. El carbono-14 sufre una desintegración radiactiva una vez que la planta o el animal muere, y la medición de la cantidad de carbono-14 en una muestra transmite información sobre cuándo murió la planta o el animal.
A continuación se muestran tres fórmulas equivalentes que describen el decaimiento exponencial:
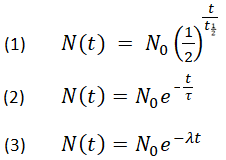
- donde
N0 es la cantidad inicial
Nt es la cantidad restante después del tiempo, t
t1/2 es la vida media
τ es el tiempo de vida medio
λ es la constante de decaimiento
Si un arqueólogo encuentra una muestra fósil que contiene un 25% de carbono-14 en comparación con una muestra viva, el momento de la muerte de la muestra fósil podría determinarse reordenando la ecuación 1, ya que se conocen Nt, N0 y t1/2.
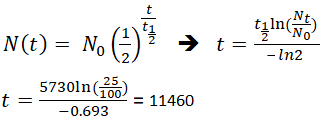
Esto significa que el fósil tiene 11.460 años.
Derivación de la relación entre las constantes de vida media
Usando las ecuaciones anteriores, también es posible que se derive una relación entre t1/2, τ y λ. Esta relación permite determinar todos los valores, siempre que se conozca al menos uno.