Cinemática rotacional - Física 298

«Los hombres hablan de matar el tiempo, mientras que el tiempo los mata tranquilamente»
Dion Boucicault – London Assurance (1841)

Hasta ahora hemos considerado la cinemática y la dinámica de las partículas, incluyendo el movimiento traslacional y circular, así como el movimiento traslacional de sistemas de partículas (en particular de cuerpos rígidos) en términos del movimiento del centro de masa del sistema (cuerpo). En este último caso podemos imaginar que toda la masa del objeto se encuentra en el centro de masa en lo que respecta a las fuerzas externas de traslación.

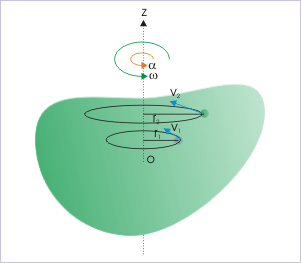El siguiente paso es considerar la rotación de un cuerpo rígido alrededor de un eje de rotación fijo. Nótese que, como estamos considerando un cuerpo rígido, cada partícula del cuerpo permanece fija con respecto a las demás. Esto significa que en tal movimiento de rotación cada partícula se mueve en un círculo cuyo centro se encuentra en el eje de rotación. En el diagrama de la derecha el objeto gira alrededor del eje z; las dos partículas de la muestra se mueven en círculos con radios r1 y r2. Si podemos describir el movimiento circular de una partícula, sin referencia directa a su radio, entonces todas las partículas del sistema serán descritas por el mismo conjunto de ecuaciones. Aunque los radios de las partículas sean diferentes, sus rotaciones angulares son idénticas. Por lo tanto, es necesario introducir variables angulares.

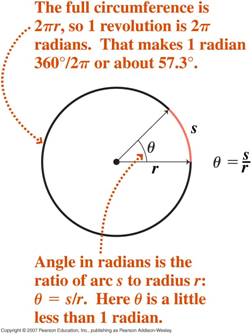
Medida del radián de los ángulos

Velocidad angular (velocidad) y aceleración angular

La velocidad angular y la aceleración angular se definen de forma similar a la velocidad y la aceleración. Hay valores medios e instantáneos de cada una.

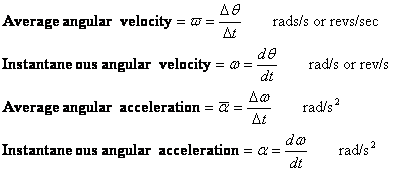
La aceleración angular no es lo mismo que la aceleración centrípeta. La aceleración centrípeta se debe a un cambio en la dirección de la velocidad, la aceleración angular se debe a un cambio en la magnitud de la velocidad (a través del ángulo de rotación).

Exactamente como en el caso traslacional, la diferencia entre la velocidad angular y la velocidad angular es la dirección. La velocidad angular debe incluir una dirección de rotación sobre el eje en cuestión. Por ejemplo, 10 rad/s en el sentido de las agujas del reloj sobre el eje x es una velocidad angular, 10 rad/s sobre el eje x es una velocidad angular.

Ecuaciones cinemáticas rotacionales

Por analogía directa con las ecuaciones cinemáticas traslacionales, el movimiento circular alrededor de un solo eje bajo aceleración angular constante puede describirse mediante las siguientes cuatro ecuaciones,

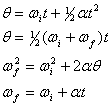
Donde hemos hecho las sustituciones,

Nótese que al igual que +x se define arbitrariamente hacia la derecha, el valor positivo de theta puede definirse como en el sentido de las agujas del reloj o en sentido contrario.

Relación entre las variables angulares y traslacionales

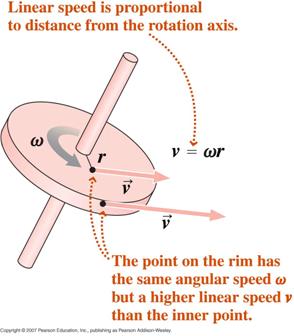A partir de la definición de medida del radián, diferenciando con respecto al tiempo, podemos demostrar que,

donde v es la velocidad tangencial y a es la aceleración tangencial.

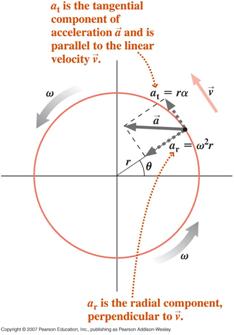
Una partícula que ejecuta un movimiento circular, con una velocidad angular variable (movimiento circular no uniforme), experimentará dos componentes de aceleración, una componente tangencial debida a la magnitud cambiante de su velocidad y una componente radial (centrípeta) debida a la dirección cambiante de su velocidad

La aceleración neta de la partícula es la suma vectorial de estas dos componentes como se indica a continuación.

Para su información…

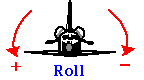
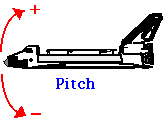
La rotación simultánea sobre más de un eje puede considerarse de forma similar al movimiento de los proyectiles, donde extendimos nuestra discusión traslacional 1D al movimiento 2D. En las aplicaciones aeronáuticas las rotaciones sobre los tres ejes se describen como Roll, Pitch y Yaw.