AC, eller vekselstrøm, har fået sit navn, fordi strømmen skifter mellem to polariteter. Med andre ord er strømmen (og dermed også spændingen) en funktion af tiden. Dette er fundamentalt forskelligt fra jævnstrøm, som er fast polaritet og generelt konstant over tid. En jævnspændingskilde i et laboratorium opretholder f.eks. ideelt set en fast spænding over sine terminaler og varierer ikke over tid. Når en vekselstrømsbølgeform derimod svinger frem og tilbage gennem tiden, kan dens form udvise store variationer, der spænder fra de enkle, regelmæssige baner i laboratoriestandarder som f.eks. sinusbølger, trekantbølger og firkantbølger til de langt mere komplekse og bølgende bølgeformer, der frembringes af musikinstrumenter og den menneskelige stemme.
Sinusbølgen er den enkleste bølge, der kan skabes. Den repræsenterer bevægelsen af en simpel vektor, der roterer med en konstant hastighed, som f.eks. den vertikale forskydning af sekundviseren på et ur. Et eksempel er vist i figur \(\PageIndex{1}\). Den vandrette akse viser tiden. Den stiger, når vi bevæger os fra venstre mod højre (dvs. hvis punkt A ligger til højre for punkt B, så forekommer A senere i tiden end B). Den lodrette akse er her generelt repræsenteret som en procentdel af maksimum, men ville normalt være en måling af spænding, strøm, lydtryk eller lignende.
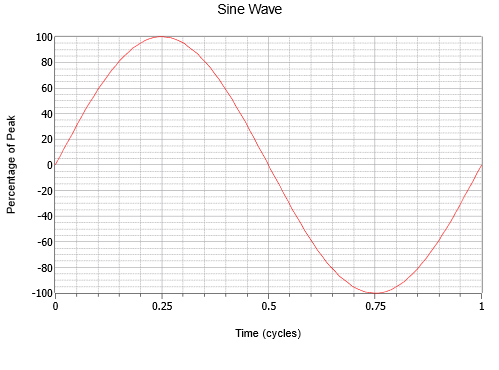
Figur \(\PageIndex{1}\): En sinuskurve.
Bemærk den jævne variation, der starter ved nul, stiger til et positivt toppunkt en fjerdedel af vejen, falder tilbage til nul efter halvvejs, fortsætter til et negativt toppunkt tre fjerdedele af vejen og stiger derefter igen til det sted, hvor den startede. Denne proces gentager sig derefter. Hver gentagelse betegnes som en cyklus. I figur \(\PageIndex{1}\) er der vist en komplet cyklus.
Sinusbølger udviser kvartbølgesymmetri. Det vil sige, at hvert kvartal (i tid) af bølgen er identisk med ethvert andet, hvis man blot vender den rundt om den vandrette akse og/eller roterer den opad om dens toppunkt. Den tid, det tager at gennemføre en cyklus, kaldes perioden og betegnes med symbolet \(T\) (for Time). Det reciprokke af perioden er frekvensen, \(f\).
\
Frekvensen angiver, hvor mange cyklusser der findes i et sekund. For at ære en af 1800-tallets forskere på området bruger vi i stedet for at kalde enheden “cyklusser pr. sekund” Hertz, opkaldt efter Heinrich Hertz og forkortet Hz. I figur \(\PageIndex{2}\) er vist tre sinusbølger med forskellige frekvenser; den oprindelige bølge (grøn), en bølge med dobbelt frekvens (blå) og en tredje med halv frekvens eller dobbelt periode (rød).
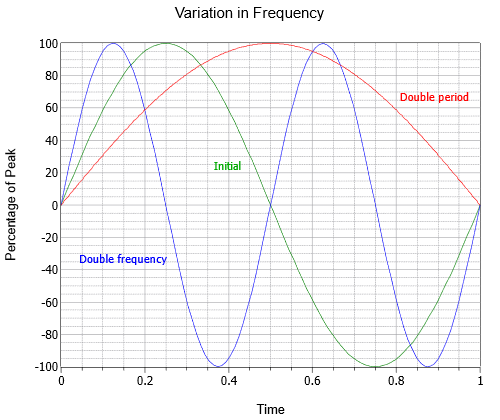
Figur \(\PageIndex{2}\): Sinusbølgens frekvensvariation.
Bølgens amplitude (lodret) kan udtrykkes som en topmængde, som er ændringen fra den midterste nullinje op til den mest positive værdi. Amplitude kan også udtrykkes som peak-to-peak; afstanden fra den mest negative til den mest positive værdi. For en sinusbølge vil dette altid være det dobbelte af topværdien, selv om det måske ikke er tilfældet for andre bølger, som kan være asymmetriske. En serie af tre sinusbølger med forskellige amplituder er vist i figur \(\PageIndex{3}\). Ved siden af den oprindelige (grøn) er der en version med dobbelt amplitude (blå) og en version med halv amplitude (rød).
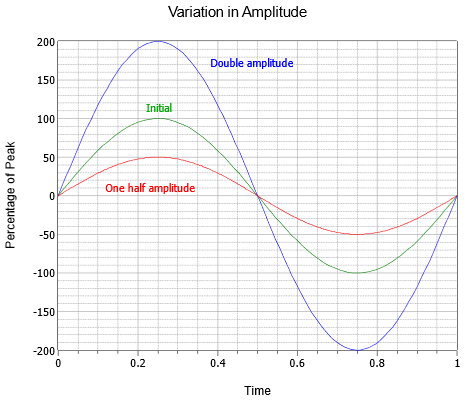
Figur \(\PageIndex{3}\): Hvis man kombinerer disse parametre, kan man se på den spændingsbølgeform, der er vist i figur \(\PageIndex{4}\). Her ser vi to cyklusser af en vekselspændingsbølgeform.
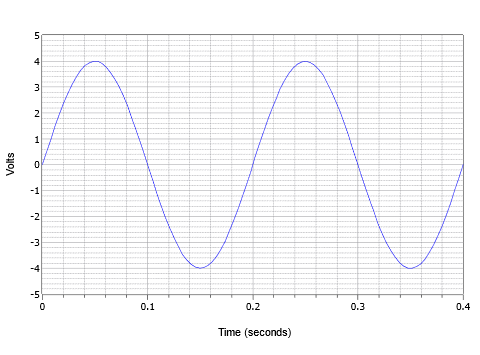
Figur \(\PageIndex{4}\): Grundlæggende sinusbølgeeksempel.
Topværdien er 4 volt og peak-to-peak-værdien er 8 volt (typisk forkortet som “8 V pp”). Perioden for en cyklus er 0,2 sekunder eller \(T = 200\) millisekunder. Endvidere er frekvensen \(f = 1/200\) millisekunder, eller 5 Hz (5 cyklusser i et sekund).
AC-bølgeformer kan også kombineres med en DC-offset. Tilføjelse af et positivt DC-niveau forskyder bølgen lodret opad, mens et negativt DC-niveau forskyder bølgen lodret nedad. Dette ændrer ikke frekvensen eller vekselstrømsdelen af amplituden (selv om de absolutte toppe vil blive forskudt med DC-værdien). Figur \(\PageIndex{5}\) viser virkningen af forskellige DC-offsets. Over den oprindelige bølge (grøn) er der en ellers identisk bølge med en positiv DC-offset svarende til 20 % af den oprindelige topværdi (blå). Under den oprindelige bølge er der en tredje bølge (rød), der har en negativ DC-offset svarende til halvdelen af den oprindelige toppunktsværdi.
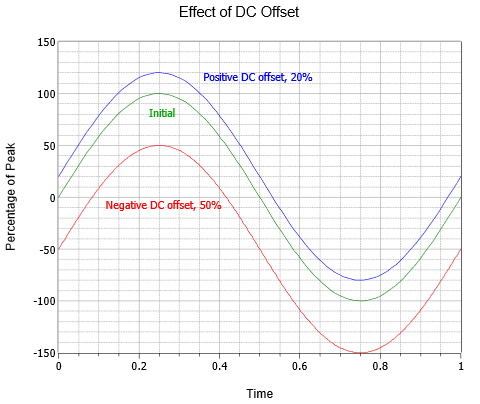
Figur \(\PageIndex{5}\): Sinusbølge DC offset variation.
Det er endvidere muligt for en sinusbølge at være forskudt i tid i forhold til en anden sinusbølge eller en reference. Selv om det er muligt at angive denne forskydning som en absolut tid, er det mere almindeligt at gøre det som en faseforskydning, dvs. tiden udtrykt som en del af perioden i grader. Hvis en sinus f.eks. er en fjerdedel af perioden foran en anden, siger man, at den er foran med 90\(^{\circ}\) (dvs. 1/4 af 360\(^{\circ}\)). Hvis den er bagud med ½ af perioden, siges den at være bagud med 180\(^{\circ}\) (dvs. 1/2 cyklus senere i tiden). En anden måde at sige det på er, at ledende bølgeformer starter tidligere i tiden og derfor tegnes til venstre for referencen, mens efterslæbende bølgeformer starter senere i tiden og tegnes til højre.
Figur \(\PageIndex{6}\) illustrerer virkningen af faseforskydning. Bemærk, at \(t = 0\) i dette plot er blevet flyttet til midten af den vandrette akse. Den midterste kurve er den oprindelige bølge eller referencebølge (grøn). Til venstre (rød) er en bølge, der ligger en ottendedels cyklus foran den oprindelige bølge, eller 45\(^{\circ}\). Til højre (blå) er en bølge, der er halvt så meget bagud, eller -22,5\(^{\circ}\).
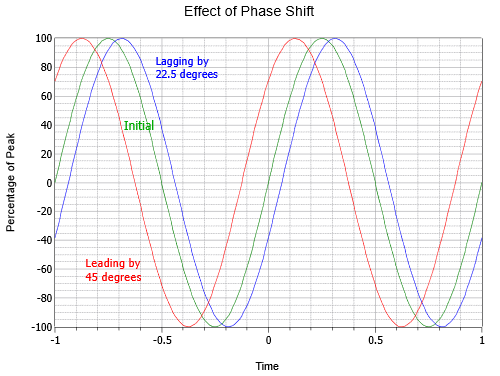
Figur \(\PageIndex{6}\): Sinusbølgens fasevariation.
Gennem at kombinere de foregående elementer kan vi udvikle et generelt format for en sinusbølge (spænding vist):
Hvor
\(v(t)\) er spændingen på et tidspunkt \(t\),
\(V_{DC}\) er den eventuelle DC-offset,
\(V_{P}\) er spidsværdien,
\(f\) er frekvensen,
\(\theta\) er faseforskydningen (+, hvis den er førende og tegnet til venstre, -, hvis den er bagud og tegnet til højre).
For et hurtigt og praktisk eksempel har den bølgeform, der er vist i figur \(\PageIndex{4}\), en amplitude på 4 volts spidsværdi, en frekvens på 5 Hz og ingen DC-offset eller faseforskydning. Dens udtryk er således \(v(t) = 4 \sin (2 \pi 5 t)\)
For at beregne en faseforskydning skal du først bestemme tidsforskellen mellem bølgeformen og referencen, som vi kalder \(\Delta t\). Referencen kan være et fast punkt i tiden (f.eks. \(t = 0\)) eller en anden bølgeform. Generelt er den nemme måde at gøre dette på at måle forskellen ved nulpunktsovergangene, idet det antages, at der ikke er nogen DC-offset. Hvis der er en forskydning, foretages målingen der, hvor nulpunktet er blevet forskudt til (dvs. ved DC-offsetniveauet). Når forskellen er fundet, divideres den med perioden for at repræsentere forskydningen som en brøkdel af en periode. Da en cyklus repræsenterer en rotation af vektoren eller 360 grader, skal brøken blot ganges med 360 grader for at finde faseskiftet i grader. Udtrykt som en formel:
\
Husk, hvis bølgen er forskudt til venstre, er den førende og positiv, mens en forskydning til højre er bagud eller forsinket i tid og dermed negativ.
Eksempel \(\PageIndex{1}\)
Skriv udtrykket for den bølgeform, der er vist i figur \(\PageIndex{7}\).
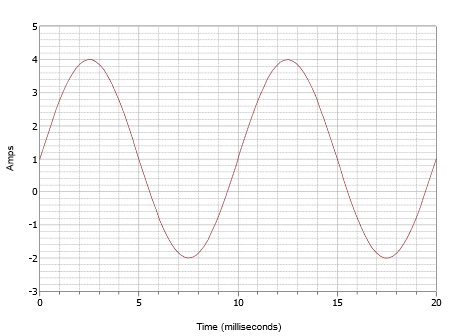
Figur \(\PageIndex{7}\): Bølgeform for eksempel \(\(\PageIndex{1}\).
Denne bølgeform kan overfladisk set ligne den i figur \(\(\PageIndex{4}\), men lad dig ikke narre af dette. Først og fremmest er tidsskalaen anderledes. For denne bølgeform er en cyklus afsluttet på 10 millisekunder. Derfor er frekvensen
\
\
\
Det andet problem er DC-offset. Bemærk, at den positive spids opstår ved 4 ampere, mens den negative spids opstår ved -2 ampere. Dette indikerer en peak-topeak-værdi på 6 ampere. Uden en offset ville den positive spids være på 3 ampere, og derfor er der en +1 ampere DC-offset. Den lodrette midte af bølgeformen er forskudt opad fra 0 ampere til +1 ampere. Dette punkt ligger ved t = 0, og der er derfor ingen faseforskydning. Det resulterende udtryk er:
\
Eksempel \(\PageIndex{2}\)
Skriv udtrykket for den bølgeform, der er vist i figur \(\PageIndex{8}\).
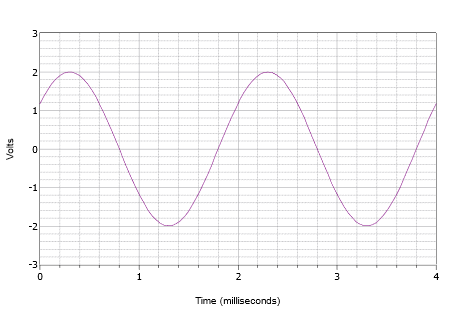
Figur \(\PageIndex{8}\): Bølgeform for eksempel \(\PageIndex{2}\).
For det første er den positive spidsværdi 2 volt, og spidsværdi-til-spidsværdi er 4 volt. Der er derfor ingen DC-offset. Bølgens lodrette centrum starter ikke ved \(t = 0\), og der må derfor være en faseforskydning. Værdien ved \(t = 0\) er 1,2 volt. Bølgen rammer denne samme amplitude ved \(t = 2\) millisekunder og begynder at gentage endnu en cyklus. Perioden må derfor være 2 millisekunder. Frekvensen er det reciprokke af denne værdi, dvs. \(f = 500\) Hz.
Bølgeformen er forskudt til venstre, hvilket indikerer en positiv eller ledende faseforskydning. Hvis vi undersøger den anden cyklus, ser vi, at den rammer nul volt ved 1,8 millisekunder. Derfor er forskydningen 0,2 millisekunder. Udtrykt i grader er dette:
\
\
\
Det endelige udtryk er:
\
Eksempel \(\PageIndex{3}\)
Tegn den bølgeform, der svarer til følgende udtryk.
\
Først skal du bemærke, at forskydningen på -3 volt skubber den positive spids ned fra 5 volt til 2 volt, og den negative spids ned fra -5 volt til -8 volt. Frekvensen på 40 kHz dikterer en periode på:
Faseskiftet på -72\(^{\circ}\) svarer til 72/360 eller 0,2 cyklusser. Dette svarer til en tidsforsinkelse (forskudt til højre, fordi den er negativ) på 0,2 gange 25 \(\mu\)s, eller 5 \(\mu\)s.
I første omgang er det ofte bedst at konstruere plottet via en række diskrete trin i stedet for at forsøge at tegne det hele på én gang. Først tegnes en sinuskurve med en spidsamplitude på 5 volt og en periode på 25 \(\mu\)s. Nu skubbes bølgeformen 3 volt nedad, så den positive top kun er på 2 volt, og den negative top er nede på -8 volt. Endelig skubbes den nyligt forskudte bølgeform til højre med 5 \(\mu\)s. Resultatet er vist i figur \(\PageIndex{9}\).
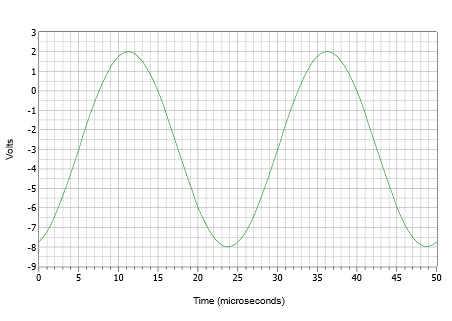
Figur \(\PageIndex{9}\): Bølgeform for eksempel \(\PageIndex{3}\).
1.2.1: Laboratoriemålinger
I laboratoriet bruges en funktionsgenerator til at generere sinus- og andre bølgeformer. Disse enheder giver mulighed for præcis kontrol af både amplitude og frekvens af bølgen sammen med tilføjelse af en DC-offset, hvis det ønskes. Et eksempel er vist i figur \(\PageIndex{10}\). Det tilsvarende måleværktøj er oscilloskopet, eller blot oscilloskopet, forkortet.

Figur \(\PageIndex{10}\): Laboratoriesignalgenerator.
Oscilloskopet er måske det mest nyttige og alsidige måleinstrument i laboratoriet. Typisk har de enten to eller fire indgangskanaler, selv om flere er mulige. Hver indgangskanal har sin egen følsomhedsjustering, og alle kanaler deler en fælles tidsreference. Displayet tegner bølgeformer på samme måde som dem, der er vist i figurerne \(\PageIndex{1}\) – \(\(\PageIndex{9}\). De kan også tegne en spænding mod en anden (X – Y-tilstand). Moderne oscilloskoper har yderligere funktioner som f.eks. automatisk måling af frekvens, amplitude, faseforskydning osv., cursorbaserede målinger og mulighed for at gemme visningsbilleder som grafikfiler. Et eksempel på et firekanals digitalt oscilloskop er vist i figur \(\PageIndex{11}\).

Figur \(\PageIndex{11}\): Et digitalt oscilloskop.
1.2.2.2: Skemasymboler
Som skemaer er symbolerne for vekselspændings- og strømkilder vist i figur \(\PageIndex{12}\). Polaritets- og retningsmarkeringerne er ikke absolutte; der er trods alt tale om vekselstrømskilder, hvis polaritet og retninger vendes frem og tilbage. Markeringerne bruges i stedet til at etablere en tidsreference, især i kredsløb, der anvender flere kilder.
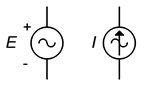
Figur \(\PageIndex{12}\): Skematiske symboler for vekselspændingskilde (venstre) og strømkilde (højre).
Det er værd at huske, at det at negere en kilde er det samme som at vende dens polaritet om. Dette gjaldt for jævnstrømskilder og gælder fortsat for vekselstrømskilder. Dette er illustreret i figur \(\PageIndex{13}\). Nogle gange vil det at vende eller negere kilden gøre analysen lidt mere indlysende eller lettere at visualisere.
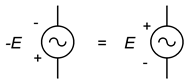
Figur \(\PageIndex{13}\):
Eksempel \(\PageIndex{4}\)
Antag, at et oscilloskop viser to bølger som vist i figur \(\PageIndex{14}\). Bestem faseforskydningen af den mindre bølgeform med 20 voltspids (blå) i forhold til den større bølgeform med 25 voltspids (rød).
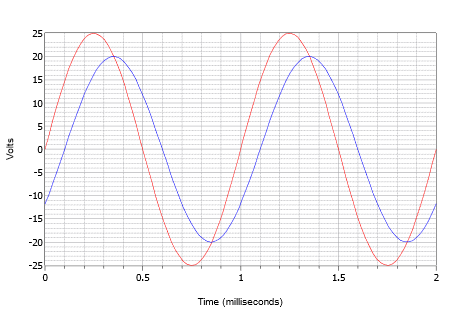
Figur \(\PageIndex{14}\): Bølgeformer for eksempel \(\PageIndex{4}\).
Først bemærkes det, at ingen af bølgerne udviser en jævnstrømsforskydning. Hvis en af dem eller begge havde en forskydning, skulle bølgen/bølgerne forskydes lodret, så deres normale nulpunktskrydsningspunkter ville være på samme niveau. Ved måling af begge bølger konstateres det, at perioden er 1 millisekund. Det er lettest at finde tidsforskydningen ved et af nulpunktskrydsene (der er fire steder at vælge imellem). Forsinkelsen er en lille afvigelse eller 0,1 millisekund, idet den mindre bølge er forsinket i tid, eller halter efter den større bølge. Dette indikerer en negativ faseforskydning.
\
\
\
1.2.3: Sinus og cosinus
Der er en håndfuld specifikke faseforskydninger, som er værd at se nærmere på. Hvis en sinuskurve er inverteret, dvs. vendt på hovedet, er den ikke til at skelne fra en sinuskurve, der er blevet forskudt enten +180 eller -180 grader. Med andre ord kan en sådan bølge skrives på tre forskellige måder: \(- \sin (2 \pi ft)\), \(\sin (2 \pi ft – 180^{\circ})\), eller \(\sin (2 \pi ft + 180^{\circ})\). Hvis en sinusbølge er forskudt med +90 grader (dvs. fremad og til venstre), kan den også betegnes som en cosinusbølge. Således er \(\sin (2 \pi ft + 90^{\circ}) = \ cos (2 \pi ft)\). Endelig kan en sinusbølge, hvis den er forskudt med -90 grader (dvs. forsinket og til højre), betegnes som en negativ eller omvendt cosinusbølge. Således er \(\sin (2 \pi ft – 90^{\circ}) = – \cos (2 \pi ft)\). Forholdet mellem disse fire bølger er illustreret i figur \(\PageIndex{15}\).
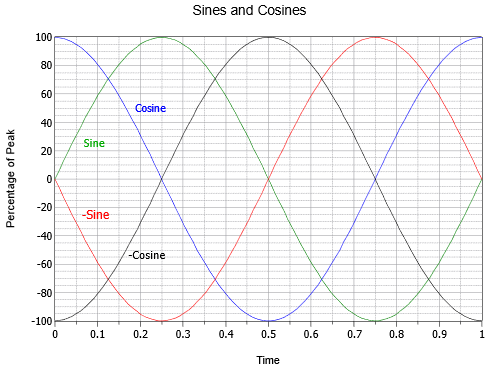
Figur \(\PageIndex{15}\): Tidsforhold mellem sinus og cosinus.
Det er også værd at bemærke, at cosinusbølgen repræsenterer den første afledte, eller hældning, af sinusbølgen. Som du måske husker fra andre studier, er hældningen eller “stejlheden” af en linje forholdet mellem den vertikale ændring og den horisontale ændring, nogle gange kaldet “stigningen over løbeforløbet”. For en spænding vil det være ændringen i spænding i forhold til ændringen i tid eller \(\Delta V/ \Delta t\). For en jævn, kontinuerligt skiftende kurve som f.eks. en sinuskurve defineres hældningen i et givet punkt korrekt som den første afledte kurve, eller \(dv/dt\) i dette tilfælde. For visuelt at kontrollere, at dette er sandt, skal man bemærke, at den stejleste del af sinusbølgen (grøn) er der, hvor den krydser nulamplituden. Når den passerer nul, mens den bevæger sig positivt (ved \(t = 0\) eller \(t = 1\) i figur \(\(\PageIndex{15}\))), er cosinus (blå) på sit positive højdepunkt. Når sinus passerer nul, mens den bevæger sig negativt (ved \(t = 0,5\)), er cosinus på sit negative højdepunkt. Endvidere er sinusbølgen flad med en hældning på nul på dens positive og negative toppunkt (ved henholdsvis \(t = 0,25\) og \(t = 0,75\)), og på disse tidspunkter er cosinus’ amplitude også nul. Det er også rigtigt, at sinusbølgen er hældningen af den negative cosinusbølge, at den negative cosinus er hældningen af den negative sinus, og at den negative sinus er hældningen af cosinus. I den omvendte retning kan vi sige, at antiderivatet (ubestemt integral) af en cosinusbølge er en sinusbølge, integralet af en sinusbølge er en negativ cosinusbølge osv. Disse forhold vil vise sig at være særdeles nyttige, når vi vender vores opmærksomhed mod kondensatorers og induktorers reaktion i vekselstrømskredsløb.
1.2.4: RMS – Root Mean Square Measurement
Sammen med peak og peak-to-peak kan amplitude angives som en RMS-værdi (Root Mean Square). Hvis peak eller peak-to-peak ikke er angivet, antages det faktisk, at målingen er RMS. RMS er en særlig beregning, der bruges til at finde ækvivalent DC-effekt (meget almindeligt, f.eks. med audio-effektforstærkere). Med andre ord, hvis vi er interesseret i at finde effekten i en modstand, skal beregningen udføres ved hjælp af RMS-værdier for spænding eller strøm, ikke peak- eller peak-to-peak-værdier. Hvis man ikke gør det, vil det resultere i fejlagtige ydelser. Dette gælder uanset bølgeformen, uanset om det er en sinusbølge, en trekantbølge eller komplekse bølger i musiksignaler. Hvis en spænding er specificeret som RMS, kan den behandles til effektberegninger på samme måde som en jævnspænding af tilsvarende størrelse. F.eks. vil en sinusspænding på 1 volt RMS give samme effektforbrug og opvarmning i en given modstand som 1 volt jævnspænding. Af denne grund omtales RMS undertiden som den effektive værdi (dvs. effektiv DC-værdi).
Navnet root-mean-square beskriver processen til bestemmelse af den effektive værdi. Først skal du huske på, at effekt er proportional med kvadratet på spændingen eller strømmen. Vores første skridt vil således være at kvadrere inputbølgeformen. Selvfølgelig er bølgeformen en funktion af tiden, og dens kvadrat vil give en ny form. På dette tidspunkt er vi nødt til at finde gennemsnitsværdien af denne nye form. Grunden til dette er enkel, men ikke nødvendigvis indlysende. Elektriske og elektroniske komponenter har masse og opvarmes eller afkøles derfor ikke øjeblikkeligt. De udviser en termisk tidskonstant. Derfor reagerer de på det gennemsnitlige input over tid. Selv om vi kan beregne en eller anden form for “øjeblikkelig spidseffekt” på et bestemt tidspunkt, repræsenterer det ikke den tilsvarende jævnstrømseffekt. Når vi har fået middelværdien af denne kvadrerede bølgeform, er den tilsvarende DC-værdi blot kvadratroden af middelværdien. Resultatet er en brøkværdi mellem nul og et, der bruges som en skaleringsfaktor til at omdanne en spidsværdi til en RMS-værdi. Værdien vil være unik for den specifikke bølgeform. Det vil sige, at alle sinusbølger (uanset fase) har den samme faktor, alle regelmæssige trekantsbølger har den samme faktor osv. Da vi for det meste beskæftiger os med sinusser, skal vi se nærmere på bestemmelsen af RMS-faktoren for dem.
Vi begynder med det grundlæggende udtryk for en sinusbølge uden DC-offset eller faseforskydning og med en amplitude på én:
\
Det første skridt er at kvadrere denne bølgeform. En nyttig trigonometrisk identitet er
Anvendelse heraf på vores bølge giver:
Dette udtryk beskriver en inverteret cosinusbølge med dobbelt så høj frekvens som den oprindelige frekvens og halvdelen af den oprindelige amplitude, der rider på en DC-offset svarende til dens topværdi. Med andre ord er den negative top af cosinusbølgen på nul og den positive top på 1. Det næste skridt er at finde gennemsnittet eller middelværdien af dette mellemliggende resultat. Middelværdien er lig med forskydningen på 0,5. Dette kan visualiseres som det område, der ligger over forskydningen, og som fuldstændig udfylder “fordybningen” under forskydningen. Det sidste trin er at tage kvadratroden af middelværdien. Kvadratroden af 0,5 er lig med 1 over kvadratroden af 2, dvs. ca. 0,707. Derfor er RMS-værdien 0,707 gange topværdien. Alternativt kan man dividere topværdien med kvadratroden af to, dvs. ca. 1,414. Denne proces er vist grafisk i figur \(\PageIndex{16}\).
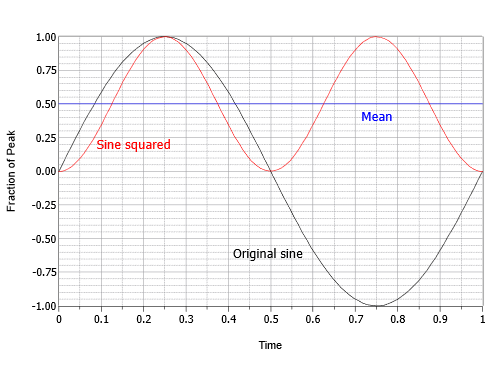
Figur \(\PageIndex{16}\): Fremgangsmåde til at finde RMS-faktor for sinusser.
For sinusbølger er RMS altid den maksimale værdi gange 0,707. Vi kan også sige, at RMS-værdien for enhver sinusbølge er dens topværdi divideret med ca. 1,414. Igen ville disse forhold ikke nødvendigvis være gældende for ikke-sinusbølger. Nærmere oplysninger om andre almindelige former kan findes i tillæg C. Endelig kaldes forholdet mellem toppunktsværdien og RMS-værdien for toppunktsforholdet. Dette er en fast værdi for sinusbølger (igen ca. 1,414), men kan være over 10:1 for visse former for lydsignaler.
1.2.5: Bølgelængde
Et andet punkt af interesse er bølgens udbredelseshastighed. Denne varierer meget. I tilfælde af lys i et vakuum (eller tilnærmelsesvis en elektrisk strøm i en ledning) er hastigheden ca. 3E8 meter i sekundet (dvs. 300.000 km/s) eller ca. 186.000 miles i sekundet.
Givet en hastighed og en periode kan vi forestille os, hvor langt bølgetoppene er fra hinanden. Denne afstand kaldes bølgelængden og betegnes med det græske bogstav lambda \(\lambda\). Bølgelængden er lig med hastigheden divideret med frekvensen, \(\lambda = v/f\). For en højttaler, der frembringer en sinus på 100 Hz, er lydhastigheden i luft 344 m/s, og derfor er \(\lambda = 344 m/s \, / \, 100\) Hz, eller 3,44 meter (lidt over 11 fod). Bemærk, at jo højere frekvensen er, jo kortere er bølgelængden. Bemærk også, at jo hurtigere hastigheden er, jo længere bølgelængde. Bølgelængdeberegninger er af særlig betydning inden for telekommunikation og akustik.