Alle elektroner i et atom kan identificeres entydigt ved hjælp af et sæt af fire kvantetal.

Selv om deres opdagelse krævede avanceret matematik, er de alle konventionelle tal: tre af dem kan kun antage simple heltalsværdier; det fjerde er en simpel brøk.
De tre første kvantetal stammer fra bølgefunktionen, Ψ, som fås ved at løse Schrödinger-ligningen.
Det fjerde kvantetal, elektronspin, stammer fra opdagelsen af, at elektroner har to mulige orienteringer.
Tallene og deres definitioner er som følger:
Kvantetallene
| Kvantetal | Navn | Mulige værdier | Information |
|---|---|---|---|
| n | Principielt kvantetal | 1, 2, 3,…, n | Definerer den energiskal, som elektronen besætter. Skaller nærmest kernen har den laveste værdi af n og den laveste potentielle energi.n er det første tal, der skrives i elektronkonfigurationer som f.eks. magnesiums: 1s2 2s2 2p6 3s2 |
| l | orbital vinkelimpuls kvantetal (også kaldet det azimutale kvantetal) |
0, 1, 2,…, (n-1) | Definerer energiunderskallen – i systemer med mere end én elektron har underskallerne forskellige energier. l definerer underskallenbogstavet i elektronkonfigurationer. F.eks: 1s2 2s2 2p6 3s2 l = 0 giver en s-underskal. l = 1 giver en p-underskal. l = 2 giver en d-underskal osv. |
| ml | magnetisk kvantetal | -l, (l+1), …, 0, …. , (l+1), l | Definerer orienteringen af subshellorbitalet. Den p subshell, med l = 1, har tre ml-værdier: Disse angiver, at der findes tre p-orbitaler, dvs. orbitalerne px, py og pz. Den d-underskal, med l = 2, har fem ml-værdier: -Disse angiver, at der findes fem d-orbitaler. |
| ms | elektronernes spinkvantetal | -½ eller +½ | Elektroner har to mulige spinorienteringer. |
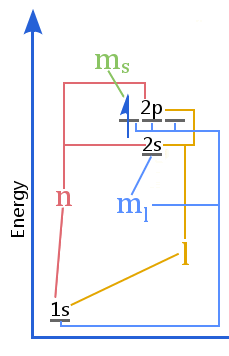
Energiniveaudiagrammet viser forholdet mellem kvantetal vs. skaller, underskaller, orbitaler og elektronspin i et atom.
Ingen elektron i et atom deler alle fire kvantetal.Hver elektron kan entydigt identificeres ved sit kvantetal – se Pauli-eksklusionsprincippet.
Orbitalernes form er ikke givet af kvantetallene, men er sandsynlighedstætheder – tredimensionelle kort over det rum omkring kernen, hvor en elektron vil befinde sig i 99 procent af tilfældene.Orbitalformerne fås ud fra kvadratet på bølgefunktionen, Ψ2.Den præcise placering og impuls af en elektron kan aldrig kendes – se Heisenbergs usikkerhedsprincip.
