Koordinattransformationer

Indledning

Koordinattransformationer er uintuitivt nok i 2-D, og positivt smertefuldt i 3-D. Denne side behandler dem i følgende rækkefølge: (i) vektorer i 2-D, (ii) tensorer i 2-D, (iii) vektorer i 3-D, (iv) tensorer i 3-D, og endelig(v) tensortransformationer af 4. rang.
Et vigtigt aspekt af koordinattransformationer er evalueringen af transformationsmatrixen, især i 3-D. Dette berøres her og diskuteres udførligt på næste side.
Det er meget vigtigt at erkende, at alle koordinattransformationer på denne side er rotationer af koordinatsystemet, mens selve objektet forbliver fast. “Objektet” kan være en vektor, f.eks. kraft eller hastighed, eller en tensor, f.eks. spænding eller belastning i en komponent. Objektrotationer behandles i senere afsnit.

2-D-koordinattransformationer af vektorer

Den akademiske kartoffel giver et glimrende eksempel på, hvordan koordinattransformationeranvendes på vektorer, samtidig med at det understreges, at det er koordinatsystemet, der roterer, og ikke vektoren … eller kartoflen.
Kartoflen til venstre har en vektor på sig. Men uden et koordinatsystem er der ingen måde at beskrive vektoren på.Så der er blevet tilføjet et koordinatsystem til kartoflen som vist til højre, så vektoren nu kan beskrives som \({\bf v} = 2{\bf i} + 9{\bf j}\)\.

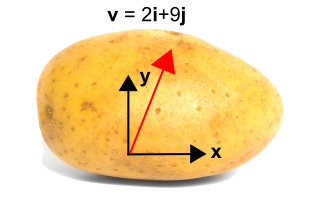
Så nu indfører vi et roteret koordinatsystem vist med blå farve nedenfor, idet vi bruger\(x’\) og \(y’\). Det nye system er roteret mod uret med en vinkel, \(\theta\),i forhold til det oprindelige koordinatsystem. Bemærk, at selve vektoren ikke ændres overhovedet. Den er stadig den samme vektor som før. Men den beskrives med andre numeriske værdier i det nye koordinatsystem. I dette tilfælde er vektoren mere parallel med den nye \(x’\)-akse end \(y’\)-aksen, så \({\bf i’}\)-komponenten vil være større end \({\bf j’}\)-komponenten. Transformationen er givet under figuren.
De 2-D vektortransformationsligninger er

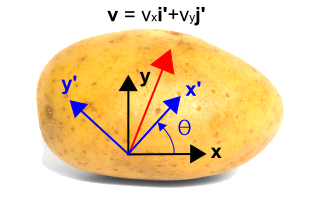
Dette kan ses ved at bemærke, atDisse fire faktorer udgør de fire termer i transformationsligningerne. De kan let kontrolleres ved at sætte \(\theta = 0^\cirk \) og \(\theta = 90^\cirk \). Når \(\theta = 0^\circ\), så er \(v’_x = v_x\) og \(v’_y = v_y\). Når \(\theta = 90^\circ\), så er \(v’_x = v_y\) og \(v’_y = -v_x\).

Transformationsmatrix

Det er mere praktisk at skrive (og arbejde med) transformationsligninger ved hjælp af matricer.
\\\left\{ \matrix {v_x \\\ v_y} \right\}}]
De \(\cos \theta\) termer er på matrixdiagonalen, mens de \(\sin \theta\)termer er uden for diagonalen. Det eneste potentielle problem er at huske, hvilket \(\sin \theta\)-term der har et minustegn på. Det er altid den nederste venstre term.

Overstående ligning skrives i matrixnotation som

hvor \({\bf Q}\) er det sædvanlige bogstav, der er valgt for transformationsmatrixen.

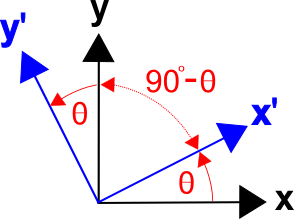
Der findes en generel metode til at formulere transformationsmatricer baseret på cosinus af vinklerne mellem akserne i de to koordinatsystemer, dvs. retningskosinus. (Dette gælder også for 3D-transformationer.)Transformationsmatrixen kan skrives som
\\\]
hvor \((x’,x)\) repræsenterer vinklen mellem akserne \(x’\) og \(x\),\((x’,y)\) er vinklen mellem akserne \(x’\) og \(y\) osv.
Vinklen mellem \(x’\) og \(y\) er \((90^\circ – \theta)\), og \(\cos(x’,y) = \cos(90^\circ – \theta) = \sin \theta\).
Sådan er vinklen mellem \(y’\) og \(x\) \((90^\circ + \theta)\), og \(\(\cos(y’,x) = \cos(90^\circ + \theta) = -\sin \theta\).

Tensornotation

Koordinattransformationen skrives i censornotation som
\
hvor \(\(\lambda_{ij}\) er transformationsmatrixen \({\bf Q}\). (Jeg ved ikke, hvorfor\({\bf Q}\) bruges i matrixnotation, men \(\lambda_{ij}\), ikke \(q_{ij}\), bruges i tensor notation). \(\lambda_{ij}\) er defineret som

For eksempel, hvis \(i = 1\) og \(j = 2\), så er

\(\lambda_{ij}\) retningen cosinus af vinklen mellem \(x’_i\) aksen og \(x_j\) aksen. Igen gælder dette også for 3D-transformationer.

2-D koordinattransformationer af tensorer

Dette afsnit vil præsentere hvad og hvordan tensortransformationer foregår. hvorfor må vente til senere.
Koordinattransformationer af tensorer af 2. rang involverer den samme \({\bf Q}\)matrix som vektortransformationer. En transformation af spændingstensor \(\boldsymbol{\sigma}\) fra referencekoordinatsystemet \(x-y\) til \(\boldsymbol{\sigma’}\) i et nyt \(x’-y’\)-system foregår på følgende måde.

Skrivning af matricerne eksplicit giver
\ = \left \left \left \left \left \]
(Bemærk, at spændingstensorerne altid er symmetriske, selv efter transformationer.)
Multiplicering af matricerne giver
\
Disse tre ligninger er præcis 2D-transformationen af en spændingstensor, der fremkommer ved at summere kræfter på et differentielt element og pålægge ligevægt. Dette er også repræsenteret ved Mohrs cirkel.

Tensornotation

Koordinattransformationen skrives i censornotation som
\
Som sædvanlig giver censornotationen ekstra indsigt i processen. Denne gang kommer indsigten fra subscripts på lambdaerne. Hvert lambda parrer effektivt en subscript på \(\boldsymbol{\sigma}\) med en på \(\boldsymbol{\sigma}\), og dette gælder uanset tensorens rang.

3-D koordinattransformationer af vektorer

Mange af de generelle ligninger, der anvendes i 2D-transformationer, gælder også i 3D.Eksempler omfatter
\

Selvfølgelig er detaljerne nu anderledes. Vektorerne har z-komponenter, og transformationsmatricerne er 3×3 i stedet for 2×2.
\\]
\]
\]
\left\{ \matrix { v_x \\\ v_y \\ v_z } \right\}}\]

3-D koordinattransformationer af tensorer

Gennu en gang ændres reglerne ikke, kun detaljerne gør det.

Skrivning af matricerne eksplicit giver
\ = \left\left\left\left\]
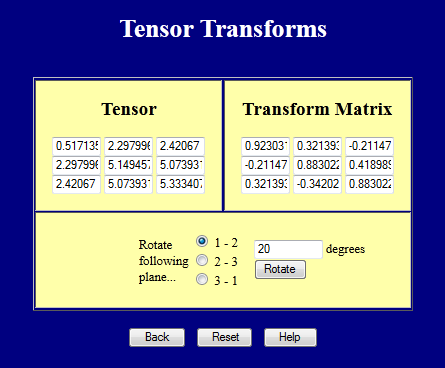
Denne webside udfører koordinattransformationer på 3-D tensorer. Prøv den.

Koordinattransformationer af tensorer af 4. rang

Vi vil se i afsnittet om Hookes lov, at stivhedstensorerne er af 4. rang, dvs. 3x3x3x3x3 (ikke 4×4). Den skrives som \(C_{ijkl}\), fordi den relaterer enhver belastningskomponent, \(\epsilon_{kl}\), til en hvilken som helst spændingskomponent, \(\sigma_{ij}\),dvs, \(\sigma_{ij} = C_{ijkl} \epsilon_{kl}\).Koordinattransformationsloven for stivhedstensoren af 4. rang kan let skrives i tensor notation som
\
Tensorligningen anviser, hvordan transformationen skal skrives i matrix notation.
\

Summarum

Koordinattransformationen af en vektor i matrix- og tensor notation er

Koordinattransformationen af en tensor i matrix- og tensor notation er

Bemærk, at \({\bf Q}\) og \(\lambda_{ij}\) er den samme transformationsmatrix.
I 2-D er \({\bf Q}\) og \(\lambda_{ij}\) defineret som
\\\]
som er et specialtilfælde af den mere generelle 3-D form
\\]