Proportional er blot en måde at reagere på en fejl i systemet på. Problemet med proportionalstyring er, at den ikke kan registrere tendenser og tilpasse sig dem. Det er den integrale styrings opgave.
Der er et andet eksempel på en graf over fejl i et system over tid til venstre i figur 6. Igen kan det være en robots afstand til et objekt, eller det kan være væskeniveauet i en tank eller temperaturen i en fabriksovn. Måske bliver det mål, som robotten følger, ved med at bevæge sig væk fra robotten med en hastighed, som robotten ikke kan indhente. Måske er ovndørens tætning slidt; måske er væsketrækningen fra tanken usædvanlig stor. Uanset årsagen er proportional ikke designet til at reagere på tendenser, og derfor kan den ikke opdage og rette problemet. Det er her, integralstyring kommer ind i billedet.
Integral måler området mellem fejlværdierne og tidsaksen. Hvis fejlen ikke vender tilbage til nul, bliver fejlområdet større og større. Højre side af figur 6 viser, hvordan integraludgangen kan reagere på denne form for tendens. Efterhånden som arealet mellem fejlkurven og tidsaksen øges, stiger outputtet proportionalt med dette areal. Som følge heraf driver udgangen aktuatoren hårdere og hårdere for at korrigere fejlen.
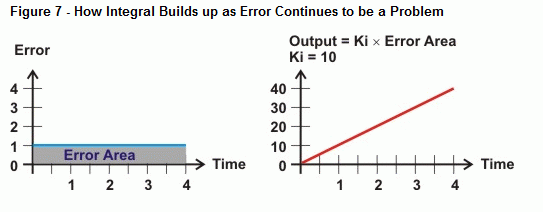
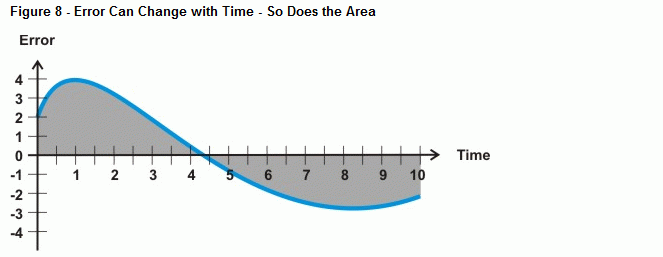
Så hvad sker der, når fejlen ikke er en lige linje, som kurven vist i figur 8? Det er det, som beregningsoperationen integration bestemmer, nemlig arealet mellem en kurve og en akse. I tilfælde af integralregulering vokser arealet under kurven, efterhånden som der går mere tid med en fejl, og det samme gør den værdi, som integralberegningen vil bruge til at køre mod systemfejlen. Hvis fejlkurven falder under tidsaksen, bliver opbygningen af det negative område trukket fra opbygningen af det positive område. Når den er indstillet korrekt, kan integralreguleringen hjælpe systemet med at skærpe sig til en fejl på nul.
BASIC-stemplet kan tilnærme sig fejlen under kurven med numerisk integration. Figur 9 viser, hvordan du kan tilnærme dig fejlen under en kurve ved at addere arealet af en række små rektangler mellem fejlkurven og tidsaksen. Arealet af hver kasse er fejlen ganget med tiden mellem målingerne. Ved at lægge alle kassearealerne sammen får du en tilnærmelse af arealet under kurven.
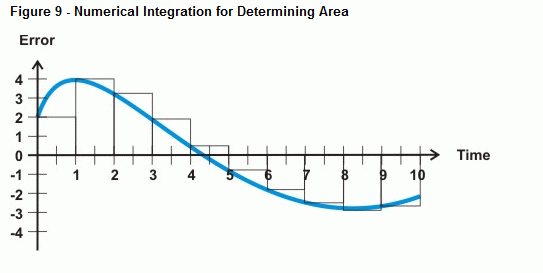
Så længe dine målinger er jævnt fordelt, kan du kalde bredden af hver kasse for en værdi på 1. Dette gør matematikken meget enklere end at forsøge at tage højde for 20 ms mellem prøverne, 5 minutter mellem prøverne, eller hvad end din samplingfrekvens viser sig at være. I stedet for at gange fejlen med tidsinkrementet mellem prøverne og derefter lægge den næste fejl multipliceret med tiden, kan du blot gange hver fejlprøve med en tid på 1. Resultatet er, at du blot kan holde en løbende total af fejlmålinger til din integralberegning. Her er et eksempel på, hvordan du kan gøre dette med PBASIC:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
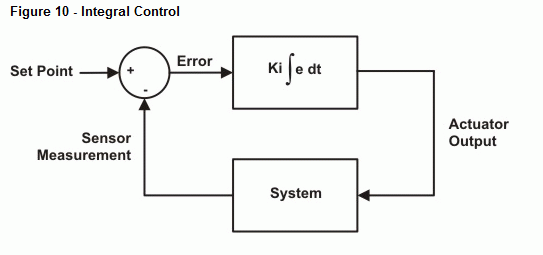
Det næste eksempelprogram udfører numerisk integration på fejlsignalet og justerer udgangen i overensstemmelse hermed. Som ved proportionalstyring er der en konstant, der skalerer integrationsoutputtet til den ønskede værdi. For enkelhedens skyld bruger vi igen 10 for Ki. Figur 10 viser et blokdiagram af reguleringssløjfen. Udtrykket Kp ∫ edt henviser til Kp multipliceret med integralet af fejlen over tiden. Med andre ord Kp ganget med det akkumulerede areal mellem fejlkurven og tidsaksen.
Eksempelprogram – IntegralAlgorithm.bs2
- Indtast, gem og kør IntegralAlgorithm.bs2.
- Indtast denne sekvens af værdier i Debugterminalens sendevinduesrude: 3 3 3 3 3 3 3 3 3. Bemærk, hvordan det integrale output bliver større, hver gang 3 gentages. Det er integralens opgave, at opdage tendenser og øge drevet for at korrigere det efter behov.
- Prøv nu denne sekvens: 1 2 3 4 5 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0. Arealet under denne kurve er 0, da det negative areal er det samme som det positive areal. Det er også det, som integralberegningen vil komme frem til, når du er færdig med at indtaste sekvensen.
' IntegralAlgorithm.bs2' Demonstrates how integral control influences error correction' in a feedback loop. ' {$STAMP BS2}' {$PBASIC 2.5} SetPoint CON 0 ' Set pointKi CON 10 ' Integral constant Current CON 0 ' Array index for current errorAccumulator CON 1 ' Array index for accumulated error sensorInput VAR Word ' Inputerror VAR Word(2) ' Two element error arrayi VAR Word ' Integral termdrive VAR Word ' Output DO DEBUG "Enter sensor input value: " DEBUGIN SDEC sensorInput ' Calculate error. error(Current) = SetPoint - sensorInput ' Calculate integral term. error(Accumulator) = error(Accumulator) + error(Current) i = Ki * error(Accumulator) ' Calculate output. drive = i ' Display values. DEBUG CR, CR, "ERROR", CR, SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR, "INTEGRAL", CR, SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR, "OUTPUT", CR, SDEC ? i, SDEC ? drive, CR, CR LOOP
Sådan fungerer IntegralAlgorithm.bs2
Dette program er et ProportionalAlgorithm.bs2 modificeret til at udføre integralberegningen i stedet. Der er nu to forskellige typer af fejl at holde styr på, så der blev fejlvariabel arrayet udvidet til to elementer. Variablen error(0) registrerer den aktuelle fejl, og error(1) registrerer den akkumulerede fejl. Konstanterne Current CON 0 og Accumulator CON 1 gør bogføringen lidt mere fornuftig med error(current) og error(accumulator).
Den anden ændring, der blev foretaget, er, at fejlen akkumuleres, og at integraludgangen beregnes med disse to udsagn:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
Din tur – klemning af integraludgangen
Som du måske har forstået ved gentagne gange at indtaste 3 i debugterminalen, kan den integrale drevudgang virkelig begynde at løbe afsted. Du kan bruge MIN- og MAX-operatorerne til at forhindre integralstyringen i at gå over gevind med udgangen. Lad os gentage servooffset-aktiviteten og begrænse output fra 650 til 850.
- Ændr drive = i-anvisningen til drive = i + Offset MIN 650 MAX 850.
- Kør programmet, og kontroller, at integraludgangen er begrænset til værdier mellem 650 og 850. Prøv at indtaste 2 gentagne gange, derefter -2 gentagne gange.