Pi formler

Der findes mange formler for af mange typer. Det drejer sig bl.a. om serier, produkter, geometriske konstruktioner, grænser, specielle værdier og pi-iterationer.

pi er intimt forbundet med egenskaberne ved cirkler og kugler. For en cirkel med radius , er omkredsen og arealet givet ved

	C			(1)
	A			(2)

Sådan er det også for en kugle med radius , er det indesluttede overfladeareal og volumen

			(3)
			(4)

En nøjagtig formel for i form af de omvendte tangenter af enhedsbrøker er Machins formel

(5)

Der findes tre andre Machin-lignende formler,samt tusindvis af andre lignende formler med flere termer.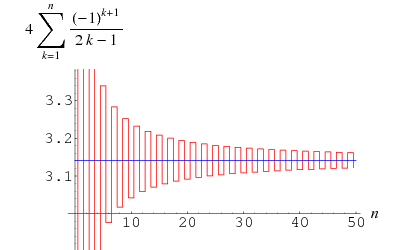

Gregory og Leibniz fandt

			(6)
			(7)

(Wells 1986, p. 50), som er kendt som Gregory-serien og kan fås ved at indsætte i Leibniz-serien for . Fejlen efter det te term i denne serie i Gregory-serien er større end , så denne sum konvergerer så langsomt, at 300 termer ikke er nok til at beregne korrekt til to decimaler! Den kan dog omdannes til

(8)

hvor er Riemanns zetafunktion (Vardi 1991, pp. 157-158; Flajolet og Vardi 1996), således at fejlen efter termer er .

En uendelig sumserie til Abraham Sharp (ca. 1717) er givet ved

(9)

(Smith 1953, p. 311). Yderligere simple serier, hvori optræder, er

1/4pisqrt(2)			(10)
			(11)
			(12)
			(13)
			(14)
			(15)
			(16)
			(17)

(Wells 1986, p. 53).

I 1666, Newton brugte en geometrisk konstruktion til at udlede formlen

			(18)
			(19)

som han brugte til at beregne (Wells 1986, p. 50; Borwein et al. 1989; Borwein og Bailey 2003, pp. 105-106). Koefficienterne kan findes ud fra integralet

			(20)
			(21)

ved at tage serieudvidelsen af omkring 0, obtaining

(22)

(OEIS A054387 og A054388). Ved hjælp af Eulers konvergensforbedringstransformation fås

			(23)
			(24)
			(25)

(Beeler et al. 1972, punkt 120).

Dette svarer til at indsætte i potensrækken for den hypergeometriske funktion ,

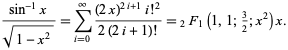(26)

På trods af konvergensforbedringen konvergerer serien (◇) kun ved én bit/termin. På bekostning af en kvadratrod har Gosper bemærket, at giver 2 bits/termin,

(27)

og giver næsten 3.39 bits/termin,

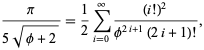(28)

hvor er det gyldne snit. Gosper fik også

(29)

En spigot-algoritme for er givet af Rabinowitz og Wagon (1995; Borwein og Bailey 2003, pp. 141-142).

Mere forbløffende endnu er det, at et udtryk i lukket form, der giver en algoritme til udtrækning af tal, som giver tal på (eller ) i base-16, blev opdaget af Bailey et al. (Bailey et al. 1997, Adamchik og Wagon 1997),

(30)

Denne formel, kendt som BBP-formlen, blev opdaget ved hjælp af PSLQ-algoritmen (Ferguson et al. 1999) og er ækvivalent med

(31)

Der findes en række formler af BBP-typen for i potenser af , hvoraf de første par uafhængige formler er

			(32)
			(33)
			(34)
			(35)
			(36)
			(37)

Sådan findes der en række formler af BBP-typen for i potenser af , hvoraf de første par uafhængige formler er

			(38)
			(39)
			(40)
			(41)
			(42)
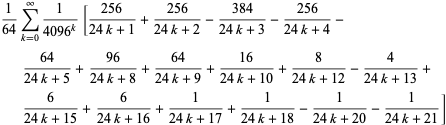			(43)
			(44)
			(45)
			(46)
			(47)
			(48)

F. Bellard fandt den hurtigt konvergerende BBP-typeformel

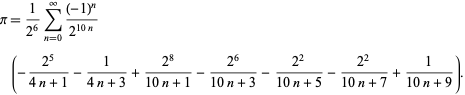(49)

Et beslægtet integral er

(50)

(Dalzell 1944, 1971; Le Lionnais 1983, s. 22; Borwein, Bailey og Girgensohn 2004, p. 3; Boros og Moll 2004, p. 125; Lucas 2005; Borwein et al. 2007, p. 14). Denne integral var kendt af K. Mahler i midten af 1960’erne og optræder i en eksamen ved University of Sydney i november 1960 (Borwein, Bailey og Girgensohn, s. 3). Beukers (2000) og Boros og Moll (2004, s. 126) anfører, at det ikke er klart, om disse findes et naturligt valg af rationelt polynomium, hvis integral mellem 0 og 1 giver , hvor 333/106 er det næste konvergente. Der findes dog et integral for den fjerde konvergent, nemlig

(51)

(Lucas 2005; Bailey et al. 2007, p. 219). Faktisk giver Lucas (2005) et par andre sådanne integraler.

Backhouse (1995) brugte identiteten

			(52)
			(53)
			(54)

for positive hele tal og , og hvor , og er rationelle konstanter til at generere et antal formler for . Især, hvis , så er (Lucas 2005).

En lignende formel blev efterfølgende opdaget af Ferguson, hvilket fører til et todimensionalt gitter af sådanne formler, som kan genereres af disse to formler givet ved

(55)

for enhver kompleks værdi af (Adamchik og Wagon), hvilket giver BBP-formlen som det særlige tilfælde .

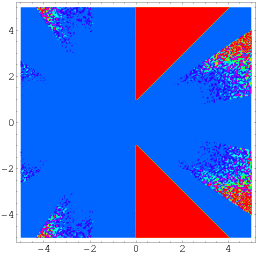
En endnu mere generel identitet, der skyldes Wagon, er givet ved

(56)

(Borwein og Bailey 2003, p. 141), som gælder over et område af det komplekse plan, der udelukker to trekantede dele, der er symmetrisk placeret omkring den reelle akse, som illustreret ovenfor.

En måske endnu mere fremmedartet generel klasse af identiteter er givet ved

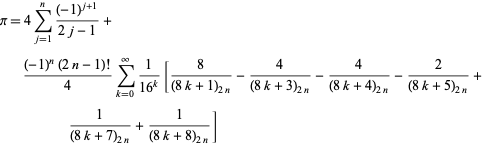(57)

som gælder for ethvert positivt helt tal , hvor er et Pochhammer-symbol (B. Cloitre, pers. comm., Jan. 23, 2005). Endnu mere forbløffende er det, at der findes en nært analog formel for den naturlige logaritme af 2.

Efter opdagelsen af BBP-formlen med 16-cifrede tal i base 16 og beslægtede formler blev lignende formler i andre baser undersøgt. Borwein, Bailey og Girgensohn (2004) har for nylig vist, at ikke har nogen BBP-arktangentformel af Machin-typen, der ikke er binær, selv om dette ikke udelukker et helt andet skema for algoritmer til udtrækning af cifre i andre baser.

S. Plouffe har udtænkt en algoritme til at beregne det te ciffer af i enhver base i trin.

Et væld af yderligere identiteter, der skyldes Ramanujan, Catalan og Newton, er givet af Castellanos (1988ab, pp. 86-88), herunder flere, der involverer summer af Fibonacci-tal. Ramanujan fandt

(58)

(Hardy 1923, 1924, 1999, p. 7).

Plouffe (2006) har fundet den smukke formel

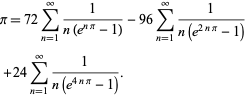(59)

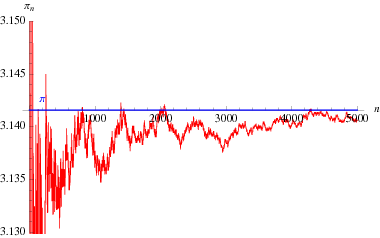
En interessant uendelig produktformel, der skyldes Euler, og som relaterer og det te primtal , er

			(60)
			(61)

(Blatner 1997, p. 119), plottet ovenfor som en funktion af antallet af termer i produktet.

En metode svarende til Archimedes’ kan bruges til at estimere ved at starte med en -gon og derefter relatere arealet af efterfølgende -gon’er. Lad være vinklen fra centrum af et af polygonens segmenter,

(62)

så

(Beckmann 1989, pp. 92-94).

Vieta (1593) var den første til at give et eksakt udtryk for ved at tage i ovenstående udtryk, hvilket giver

(64)

som fører til et uendeligt produkt af nestedradikaler,

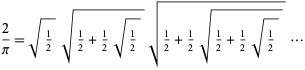(65)

(Wells 1986, p. 50; Beckmann 1989, p. 95). Det blev dog ikke strengt bevist, at dette udtryk konvergerer før Rudio i 1892.

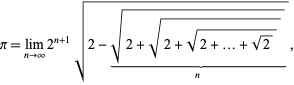
En beslægtet formel er givet ved

(66)

hvilket kan skrives

(67)

hvor er defineret ved hjælp af iterationen

(68)

med (J. Munkhammar, pers. komm, April 27, 2000). Formlen

(69)

er også nært beslægtet.

En smuk formel for er givet ved

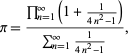(70)

hvor tælleren er en form af Wallis-formlen for og nævneren er en teleskopisk sum med sum 1/2, da

(71)

(Sondow 1997).

Et særligt tilfælde af Wallis-formlen giver

(72)

(Wells 1986, p. 50). Denne formel kan også skrives

(73)

hvor betegner en binomialkoefficient, og er gammafunktionen (Knopp 1990). Euler opnåede

(74)

hvilket følger af den særlige værdi af Riemanns zeta-funktion . Lignende formler følger af for alle positive hele tal .

En uendelig sum, der skyldes Ramanujan, er

(75)

(Borwein et al. 1989; Borwein og Bailey 2003, p. 109; Bailey et al.2007, p. 44). Yderligere summer er givet i Ramanujan (1913-14),

(76)

og

			(77)
			(78)

(Beeler et al. 1972, punkt 139; Borwein et al. 1989; Borwein og Bailey 2003, p. 108; Bailey et al. 2007, p. 44). Ligning (78) er afledt af en modulær identitet af orden 58, selv om en første afledning ikke blev præsenteret før Borwein og Borwein (1987). Ovenstående serier giver begge

(79)

(Wells 1986, s. 54) som den første tilnærmelse og giver henholdsvis ca. 6 og 8 decimaler pr. term. Sådanne serier findes på grund af rationaliteten af forskellige modulære invarianter.

Den generelle form af serien er

(80)

hvor er en binær kvadratisk formdiskriminant, er j-funktionen,

			(81)
			(82)

og er Eisenstein-serier. Et klassetalsfelt omfatter algebraiske hele tal af algebraisk grad af konstanterne , , og . Af alle serier, der kun består af heltalstermer, svarer den serie, der giver flest numeriske cifre på kortest tid, til den største diskriminant i klasse nummer 1 , og den blev formuleret af brødrene Chudnovsky (1987). Den 163, der optræder her, er den samme som den, der optræder i det faktum, at (Ramanujan-konstanten) er meget tæt på at være et helt tal. På samme måde kommer faktoren fra j-funktionens identitet for . Serien er givet ved

			(83)
			(84)

(Borwein og Borwein 1993; Beck og Trott; Bailey et al. 2007, p. 44). Denne serie giver 14 cifre nøjagtigt pr. term. Den samme ligning i en anden form blev givet af brødrene Chudnovsky (1987) og bruges af Wolfram Language til at beregne (Vardi 1991; Wolfram Research),

(85)

hvor

			(86)
			(87)
			(88)

Den bedste formel for klasse nummer 2 (største diskriminant ) er

(89)

hvor

			(90)
			(91)
			(92)

(Borwein og Borwein 1993). Denne serie tilføjer ca. 25 cifre for hver yderligere term. Den hurtigst konvergerende serie for klasse nummer 3 svarer til og giver 37-38 cifre pr. term. Den hurtigst konvergerende serie for klasse nummer 4 svarer til og er

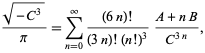(93)

hvor

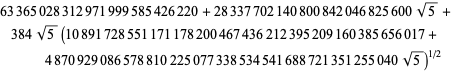			(94)
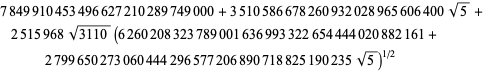			(95)
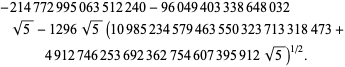			(96)

Det giver 50 cifre pr. termin. Borwein og Borwein (1993) har udviklet en generel algoritme til at generere sådanne serier for et vilkårligt klassetal.

En komplet liste over Ramanujans serier for fundet i hans anden og tredje notesbog er givet af Berndt (1994, pp. 352-354),

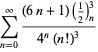			(97)
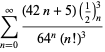			(98)
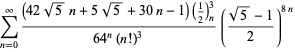			(99)
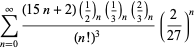			(100)
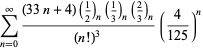			(101)
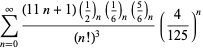			(102)
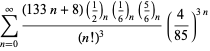			(103)
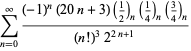			(104)
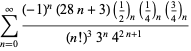			(105)
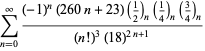			(106)
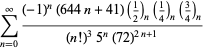			(107)
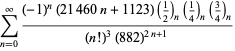			(108)
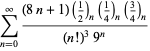			(109)
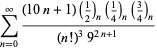			(110)
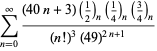			(111)
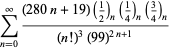			(112)
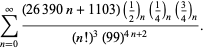			(113)

Disse ligninger blev først bevist af Borwein og Borwein (1987a, pp. 177-187). Borwein og Borwein (1987b, 1988, 1993) beviste andre ligninger af denne type, og Chudnovsky og Chudnovsky (1987) fandt lignende ligninger for andre transcendentale konstanter (Bailey et al. 2007, pp. 44-45).

En komplet liste over uafhængige kendte ligninger af denne type er givet ved

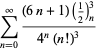			(114)
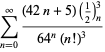			(115)
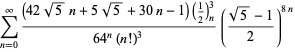			(116)
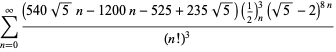			(117)
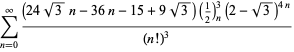			(118)

for med ikke-alternativt fortegn,

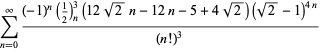			(119)
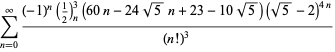			(120)
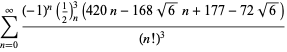			(121)
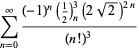			(122)

for med vekslende fortegn,

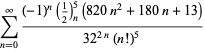			(123)
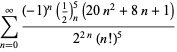			(124)

for (Guillera 2002, 2003, 2006),

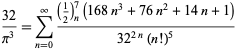(125)

for (Guillera 2002, 2003, 2006), og ingen andre for er kendt (Bailey et al. 2007, pp. 45-48).

Bellard giver den eksotiske formel

(126)

where

(127)

Gasper citerer resultatet

(128)

hvor _1F_2 er en generaliseret hypergeometrisk funktion, og transformerer det til

(129)

Et fascinerende resultat, der skyldes Gosper, er givet ved

(130)

opfylder uligheden

(131)

D. Terr (pers. komm.) bemærkede den mærkelige identitet

(132)

der involverer de første 9 cifre af pi.