Rotationskinematik - Fysik 298

“Mænd taler om at slå tiden ihjel, mens tiden stille og roligt slår dem ihjel”
Dion Boucicault – London Assurance (1841)

Selv om kinematik og dynamik for partikler, herunder translationel og cirkulær bevægelse samt translationel bevægelse af systemer af partikler (især stive legemer) i form af bevægelsen af systemets (legemets) massecentrum. I sidstnævnte tilfælde kan vi forestille os, at hele genstandens masse befinder sig i massecentret, for så vidt angår eksterne translationelle kræfter.

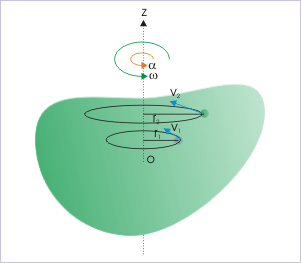Det næste skridt er at overveje rotationen af et stift legeme om en fast rotationsakse. Bemærk, at fordi vi betragter et stift legeme, forbliver alle partikler i legemet faste i forhold til de andre partikler. Det betyder, at i en sådan rotationsbevægelse bevæger hver partikel sig i en cirkel, hvis centrum ligger på rotationsaksen. I diagrammet til højre roterer objektet om z-aksen; de to prøvepartikler bevæger sig i cirkler med radius r1 og r2. Hvis vi kan beskrive en partikels cirkelbevægelse uden direkte henvisning til dens radius, vil alle partikler i systemet blive beskrevet ved hjælp af det samme sæt ligninger. Selv om partiklernes radier er forskellige, er deres vinkelrotationer identiske. Derfor er det nødvendigt at indføre vinkelvariabler.

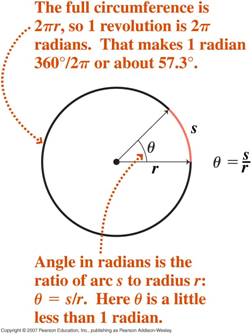
Radianmål for vinkler

Vinkelhastighed (hastighed) og vinkelacceleration

Vinkelhastighed og vinkelacceleration er defineret på samme måde som hastighed og acceleration. Der findes gennemsnitsværdier og øjeblikkelige værdier af hver af dem.

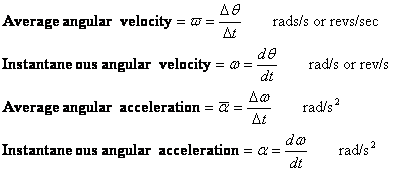
Vinkelacceleration er ikke det samme som centripetalacceleration. Centripetalacceleration skyldes en ændring i hastighedens retning, vinkelacceleration skyldes en ændring i hastighedens størrelse (gennem rotationsvinklen).

Præcis som i translationstilfældet er forskellen mellem vinkelhastighed og vinkelhastighed retningsbestemt. Vinkelhastighed skal indeholde en rotationsretning om den pågældende akse. F.eks. er 10 rad/s med uret om x-aksen en vinkelhastighed, 10 rad/s om x-aksen er en vinkelhastighed.

Rotationskinematiske ligninger

I direkte analogi med de translationskinematiske ligninger kan cirkulær bevægelse om en enkelt akse under konstant vinkelacceleration beskrives med følgende fire ligninger,

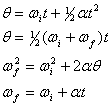
hvor vi har foretaget substitutionerne,

Bemærk, at ligesom +x er defineret vilkårligt til højre, kan den positive værdi af theta defineres som med eller mod uret.

Sammenhæng mellem vinkel- og translationsvariabler

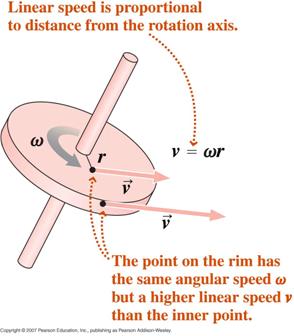Med udgangspunkt i definitionen af radianmålet kan vi ved at differentiere i forhold til tiden vise, at,

hvor v er den tangentielle hastighed og a er den tangentielle acceleration.

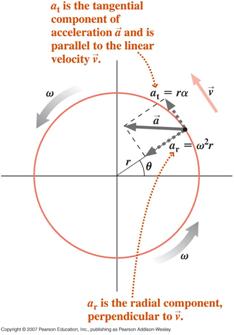
En partikel, der udfører en cirkelbevægelse med en varierende vinkelhastighed (uensartet cirkelbevægelse), vil opleve to accelerationskomponenter, en tangential komponent på grund af den ændrede størrelse af dens hastighed og en radial (centripetal) komponent på grund af den ændrede retning af dens hastighed

Partiklens nettoacceleration er vektorsummen af disse to komponenter som angivet nedenfor.

Til din information…

Samtidig rotation om mere end én akse kan betragtes på samme måde som projektilbevægelse, hvor vi udvidede vores 1D translationelle diskussion til 2D bevægelse. I aeronautiske anvendelser beskrives rotationer om de tre akser som Roll, Pitch og Yaw.