Sådan forbereder du dig på geometri-spørgsmålene i en matematikprøve
Generel information
Geometri er blot en finere betegnelse for studiet af linjer og former. Der er helt sikkert yderligere vanskelige principper og emner, men vi har grundprincipperne her. Du skal beherske disse, før du kan tage fat på mere avancerede begreber.
(Bemærk, at hvis en figur er mærket “eksempel” i denne vejledning, er det ikke nødvendigvis den eneste repræsentation af den pågældende figur, men er en af dem.)
Punkter og linjer
Et punkt i geometri er et sted. Det har ingen længde, bredde eller dybde. Vi bruger en prik og et stort bogstav til at vise et punkt.
Et linjestykke er defineret af to punkter og alle punkterne mellem dem. De to punkter kaldes segmentets endepunkter. Et segment har én dimension: længde. Hvis du vil skrive et segment, skal du placere en streg over de to endepunkter. \(\overline{AB}\) eller \(\(\overline{BA}\) er dette segment:

En linje strækker sig i begge retninger uden ende. For at skrive en linje skal du placere en streg med to pile over to vilkårlige punkter på linjen. \(\overvenstre-højre-pil{AB}\) eller \(\overvenstre-højre-pil{BA}\) er linjen:

En stråle starter ved ét endepunkt og strækker sig uden ende i kun én retning. For at skrive en stråle skal du placere en bjælke med en pil, der peger mod højre, over to punkter: endepunktet og et hvilket som helst andet punkt (i den pågældende retning). \(\overrightarrow{AB}\) er strålen:

Bemærk: Du kan ikke skrive en stråle med pilen pegende mod venstre som \(\overleftarrow{BA}\). Desuden er rækkefølgen vigtig. \(\overrightarrow{BA}\) er ikke det samme som \(\overrightarrow{AB}\). Det første bogstav er altid startpunktet for en stråle.
To linjer, segmenter eller stråler er vinkelrette, hvis de danner en ret vinkel (se nedenfor). Brug symbolet \(\perp\) til at betegne vinkelrethed. Hvis f.eks. \(\overline{AB}\) er vinkelret på \(\overline{CD}\), kan man skrive \(\overline{AB} \perp \overline{CD}\).
Eksempler: 
To linjer er parallelle, hvis de aldrig skærer hinanden. Hvis \(\overleftrightarrow{AB}\) er parallel med \(\overleftrightarrow{CD}\), kan man skrive \(\overleftrightarrow{AB} \parallel \overleftrightarrow{CD}\).
Eksempler: 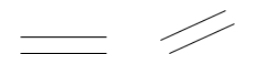
Flanke former
I geometri er et plan en flad todimensionel flade, der strækker sig uendeligt langt. De to dimensioner er længde og bredde. Plane figurer er altså “flade” figurer som f.eks. firkanter, cirkler og trekanter.
Almindelige figurer
En polygon er en lukket flade i et plan, der er afgrænset af linjestykker kaldet sider.
Eksempler: 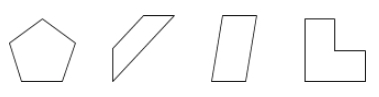
En regelmæssig polygon er en polygon, hvor alle segmenter og indvendige vinkler er kongruente.
Eksempler:
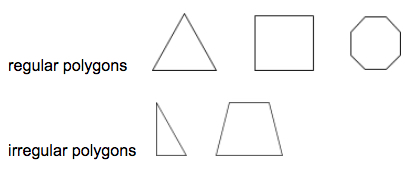
En trekant er en tresidet polygon.
Eksempler:
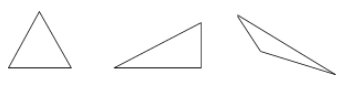
kvadrilateraler – firsidede polygoner
Et parallelogram er en type af en firkant, hvor modsatte sider er parallelle og kongruente. Modstående vinkler i et parallelogram er også kongruente.
Eksempler: 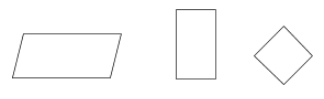
Et rektangel er et parallelogram med fire rette vinkler.
Eksempler:
Eksempler: Et rektangel er et parallelogram med fire rette vinkler: 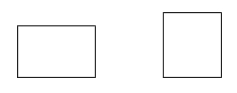
En rhombe er et parallelogram, hvor alle fire sider er kongruente.
Eksempler:
Eksempler: 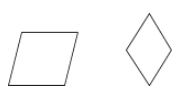
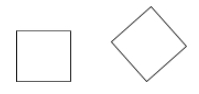
Et kvadrat er et parallelogram, som både er en rhombe og et rektangel (alle sider er kongruente, og alle vinkler er rette).
Eksempler:
Et trapez er en firkant med kun et par parallelle sider.
Eksempler:
Eksempler: Et trapez er en firkant med kun et par parallelle sider: 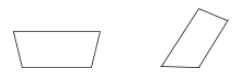
Polygoner med mere end fire sider
\
\(^1\) En polygon med 11 sider kan også kaldes en endekagon eller en undekagon.
Måling af figurer
Omkredsen er den samlede afstand omkring en polygon. For at finde omkredsen skal man blot lægge længderne af alle siderne sammen. Hvis polygonen er regelmæssig (alle sider er kongruente), og længden af en side er \(s\), skal du gange antallet af sider med \(s\) for at finde omkredsen. For eksempel er omkredsen af en regulær femkant \(P_\text{reg pentagon}=5s\)