
Neurale netværk og matematik er uadskillelige, og det er nok det, der skræmmer de fleste mennesker. Jeg har hørt en for mange tvivlsomme bemærkninger om Deep Learning: “Åh, det er for meget matematik til, at jeg kan forstå det”, “Hvor mange virksomheder bruger egentlig Deep Learning? Jeg vil hellere spare mig selv for hjernevrideriet og holde mig væk fra disse krævende koncepter”.
Men hvis man tænker over det, er det ikke så svært. Tro mig! For at forstå, hvorfor en algoritme opfører sig på en bestemt måde, er det vigtigt at forstå, hvad der sker bag kulisserne. Komplekse maskinlæringsalgoritmer er pakket bekvemt for os i dag og er kun et funktionsopkald væk. Aktiveringsfunktionernes derivater er noget mindre indlysende begreber, som vi ofte har en tendens til at ignorere. De danner imidlertid grundlaget for kraftfulde algoritmer, og det betaler sig helt sikkert at gøre en lille ekstra indsats for at forstå dem. Når du har læst denne artikel, vil du være et skridt nærmere på at opklare, hvad der ligger under facaden af “den sorte boks”.
Baggrund
Neurale netværk anvender en række aktiveringsfunktioner i de skjulte og outputlag for at katalysere indlæringsprocessen. Et par almindeligt anvendte aktiveringsfunktioner omfatter de sigmoide og tanH-funktioner. Den mest populære aktiveringsfunktion er ReLU ( Rectified Linear Unit) på grund af dens evne til effektivt at overvinde problemet med forsvindende gradient. En dybtgående indsigt i aktiveringsfunktioner er til en anden dag. I dag vil vi fokusere på matematikken bag Sigmoid-funktionens afledning.
Hvorfor er afledningen af en aktiveringsfunktion vigtig?
Som du sikkert ved, er der to trin, der driver neurale netværk:
- Forward Propagation – Inddataene strømmer gennem netværket, og vi får det forudsagte output. Vi sammenligner det med det faktiske output og beregner fejlen.
- Back Propagation – Den beregnede fejl bruges til at opdatere det neurale netværks parametre ved hjælp af den afledte aktiveringsfunktion.
Den sigmoide funktion
Den sigmoide funktion, der er kendetegnet ved en S-formet kurve, omtales ofte som et specialtilfælde af den logistiske funktion. Den er mest nyttig i tilfælde, hvor vi skal forudsige sandsynlighed som output.
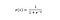
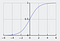
Sigmoidfunktionen udsender værdier, der ligger mellem 0 og 1 (med rette, når man tænker på, at den forudsiger sandsynligheder).
Den sigmoide afledning
Denne grundlæggende byggesten, der hjælper med at træne neurale netværk, antager formen:


Opnærmere beskrivelse, lad os komme i gang med afledningen!
Ansats 1

Ansats 2:
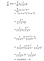
Hvorfor bruger vi denne version af afledte?
I det fremadrettede propagationstrin beregner du den sigmoide funktion (σ(x)) og har dens værdi ved hånden. Når du beregner den afledte i backpropagationstrinnet, skal du blot indsætte værdien af σ(x) i den ovenfor afledte formel, og voila, så er du klar!
Det er det, gutter! Tak fordi I læste med!