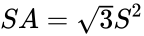For det videnskabelige tidsskrift, se Tetrahedron (tidsskrift).
| Regelmæssig tetraeder | ||
|---|---|---|
 (Klik her for roterende model) |
||
| Type | Platonisk fast stof | |
| Elementer | F = 4, E = 6 V = 4 (χ = 2) |
|
| Facetter ved siderne | 4{3} | |
| Schläfli-symbol | {3,3} og s{2,2} | |
| Wythoff-symbol | 3 | 2 3 | 2 2 2 2 |
|
| Coxeter-Dynkin | |
|
| Symmetri | Td eller (*332) |
|
| U01, C15, W1 | ||
| Egenskaber | Regelmæssig konveks deltaeder | |
| Dihedral vinkel | 70.528779° = arccos(1/3) | |
 3.3.3 (toppunktsfigur) |
 Selv-dual (dobbeltpolyeder) |
|
 Net |
||
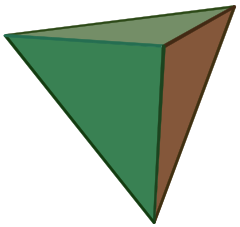
Et tetraeder (flertal: tetraeder) er et polyeder bestående af fire trekantede flader, hvoraf tre mødes i hvert toppunkt. Et regulært tetraeder er et, hvor de fire trekanter er regulære, eller “ligesidede”, og er en af de platoniske faste legemer.
Tetraederet er en slags pyramide, som er et polyeder med en flad polygonbasis og trekantede flader, der forbinder basen med et fælles punkt. I tilfældet med et tetraeder er basen en trekant (en hvilken som helst af de fire flader kan betragtes som base), hvorfor et tetraeder også kaldes trekantspyramide eller Digonal Deltahedron.
Formler for regulært tetraeder
Volumen er
Overfladearealet er
Template:Commonscat
- F. M. Jackson og Weisstein, Eric W., “Tetrahedron” fra MathWorld.
- Weisstein, Eric W., “Tetrahedron” fra MathWorld.
- Weisstein, Eric W., “Tetrahedron” fra MathWorld.
- The Uniform Polyhedra
- Tetrahedron: Interactive Polyhedron Model
- K. J. M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- Piero della Francescas formel for tetraedrons volumen på MathPages
- Gratis papirmodeller af et tetraeder og mange andre polyedre
- En forbløffende, Space Filling, Non-regular Tetrahedron, der også indeholder en beskrivelse af en “roterende ring af tetraedre”, også kendt som en kaleidocykel.
- Tetraederkernetværk Anvendelse af en tetraederstruktur til at skabe et modstandsdygtigt datanetværk med delvise masker
- Eksplicitte nøjagtige formler for en vilkårlig tetraeders inertimæssige tensor i form af dens toppunktskoordinater
- En tetraeders inertimæssige tensor