Wechselstrom wird so genannt, weil der Strom zwischen zwei Polaritäten hin und her wechselt. Mit anderen Worten: Der Strom (und folglich die Spannung) ist eine Funktion der Zeit. Dies ist ein grundlegender Unterschied zum Gleichstrom, der eine feste Polarität hat und im Allgemeinen über die Zeit konstant ist. Eine Labor-Gleichspannungsquelle beispielsweise hält im Idealfall eine bestimmte Spannung an ihren Anschlüssen aufrecht und ändert sich nicht im Laufe der Zeit. Im Gegensatz dazu kann die Form einer Wechselstrom-Wellenform, die im Laufe der Zeit hin und her schwingt, große Variationen aufweisen, die von den einfachen, regelmäßigen Bahnen von Laborstandards wie Sinuswellen, Dreieckswellen und Rechteckwellen bis hin zu den weitaus komplexeren und wellenförmigen Wellenformen reichen, die von Musikinstrumenten und der menschlichen Stimme erzeugt werden.
Die Sinuswelle ist die einfachste Welle, die erzeugt werden kann. Sie stellt die Bewegung eines einfachen Vektors dar, der sich mit konstanter Geschwindigkeit dreht, wie z. B. die vertikale Verschiebung des Sekundenzeigers einer Uhr. Ein Beispiel ist in Abbildung \(\PageIndex{1}\) dargestellt. Auf der horizontalen Achse ist die Zeit aufgetragen. Sie nimmt zu, wenn man sich von links nach rechts bewegt (d. h., wenn Punkt A rechts von Punkt B liegt, dann liegt A zeitlich später als B). Die vertikale Achse wird hier im Allgemeinen als Prozentsatz des Maximums dargestellt, wäre aber normalerweise ein Maß für Spannung, Strom, Schalldruck oder ähnliches.
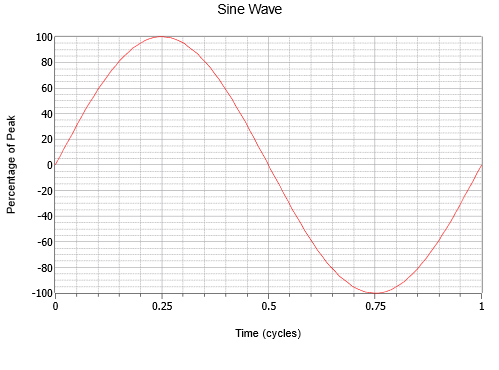
Abbildung \(\PageIndex{1}\): Eine Sinuswelle.
Beachten Sie die gleichmäßige Veränderung, die bei Null beginnt, nach einem Viertel der Strecke zu einer positiven Spitze ansteigt, nach der Hälfte der Strecke auf Null zurückfällt, nach drei Vierteln zu einer negativen Spitze ansteigt und dann wieder zum Ausgangspunkt zurückkehrt. Dieser Prozess wiederholt sich dann. Jede Wiederholung wird als ein Zyklus bezeichnet. In Abbildung \(\PageIndex{1}\) ist ein vollständiger Zyklus dargestellt.
Sinuswellen weisen eine Viertelwellensymmetrie auf. Das heißt, jedes Viertel (in der Zeit) der Welle ist mit jedem anderen identisch, wenn man sie einfach um die horizontale Achse dreht und/oder sie aufrecht um ihre Spitze dreht. Die Zeit, die für einen Zyklus benötigt wird, heißt Periode und wird mit dem Symbol \(T\) (für Zeit) bezeichnet. Der Kehrwert der Periode ist die Frequenz, \(f\).
\
Die Frequenz gibt an, wie viele Zyklen in einer Sekunde existieren. Zu Ehren eines Forschers aus dem 19. Jahrhundert nennen wir die Einheit nicht „Zyklen pro Sekunde“, sondern Hertz, benannt nach Heinrich Hertz und abgekürzt mit Hz. In Abbildung \(\PageIndex{2}\) sind drei Sinuswellen mit unterschiedlichen Frequenzen dargestellt: die Ausgangswelle (grün), eine Welle mit doppelter Frequenz (blau) und eine dritte mit halber Frequenz oder doppelter Periode (rot).
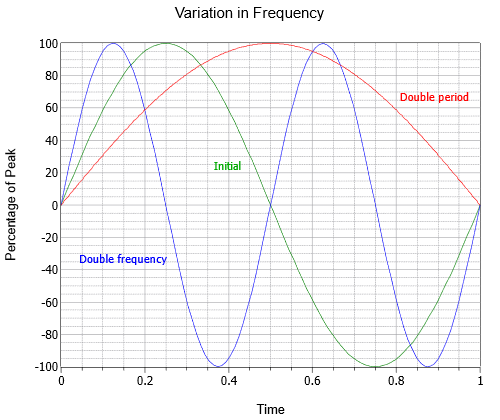
Abbildung \(\PageIndex{2}\): Sinuswellen-Frequenzverlauf.
Die Amplitude (vertikal) der Welle kann als Spitzenwert ausgedrückt werden, der die Veränderung von der mittleren Nulllinie bis zum größten positiven Wert darstellt. Die Amplitude kann auch als Peak-to-Peak ausgedrückt werden, also als Abstand vom negativsten zum positivsten Wert. Bei einer Sinuswelle ist dies immer das Doppelte des Spitzenwerts, obwohl dies bei anderen Wellen, die asymmetrisch sein können, nicht unbedingt der Fall ist. Eine Serie von drei Sinuswellen mit unterschiedlichen Amplituden ist in Abbildung \(\PageIndex{3}\) dargestellt. Neben der anfänglichen (grün) gibt es Versionen mit doppelter Amplitude (blau) und halber Amplitude (rot).
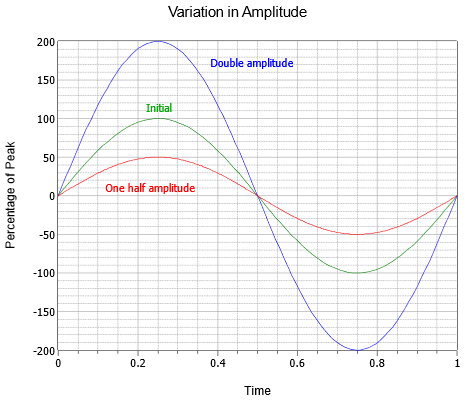
Abbildung \(\PageIndex{3}\): Variation der Sinuswellenamplitude.
Kombinieren Sie diese Parameter und betrachten Sie die in Abbildung \(\PageIndex{4}\) dargestellte Spannungswellenform. Hier sehen wir zwei Zyklen einer Wechselspannungswellenform.
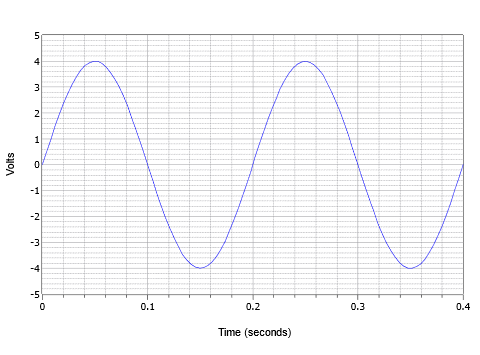
Abbildung \(\PageIndex{4}\): Beispiel einer einfachen Sinuswelle.
Der Spitzenwert beträgt 4 Volt und der Spitze-Spitze-Wert 8 Volt (üblicherweise abgekürzt als „8 V pp“). Die Periode eines Zyklus beträgt 0,2 Sekunden, also \(T = 200\) Millisekunden. Außerdem beträgt die Frequenz \(f = 1/200\) Millisekunden oder 5 Hz (5 Zyklen in einer Sekunde).
Wechselstromwellenformen können auch mit einem Gleichstrom-Offset kombiniert werden. Das Hinzufügen eines positiven Gleichstrompegels verschiebt die Welle vertikal nach oben, während ein negativer Gleichstrompegel die Welle vertikal nach unten verschiebt. Dies ändert weder die Frequenz noch den Wechselstromanteil der Amplitude (obwohl sich die absoluten Spitzenwerte um den Gleichstromwert verschieben würden). Abbildung \(\PageIndex{5}\) zeigt die Auswirkung verschiedener DC-Offsets. Über der ursprünglichen Welle (grün) befindet sich eine ansonsten identische Welle mit einem positiven DC-Offset in Höhe von 20 % des ursprünglichen Spitzenwerts (blau). Unterhalb des Originals befindet sich eine dritte Welle (rot), die einen negativen DC-Versatz aufweist, der der Hälfte des Spitzenwerts des Originals entspricht.
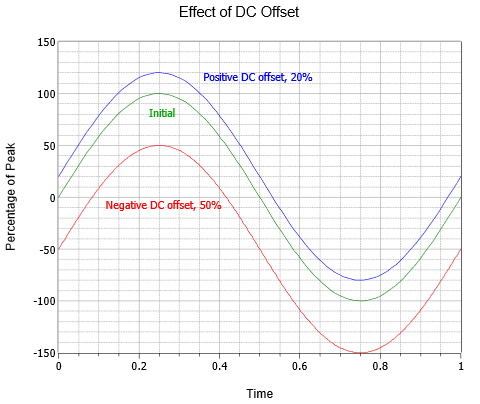
Abbildung \(\PageIndex{5}\): Sinuswellen-Gleichstrom-Offset-Variation.
Außerdem ist es möglich, dass eine Sinuswelle im Vergleich zu einer anderen Sinuswelle oder Referenz zeitlich verschoben ist. Es ist zwar möglich, diese Verschiebung als absolute Zeit anzugeben, doch ist es üblicher, dies als Phasenverschiebung zu tun, d. h. die Zeit wird als Teil der Periode in Grad ausgedrückt. Wenn zum Beispiel ein Sinus einem anderen um ein Viertel der Periode voraus ist, spricht man von einem Vorsprung von 90\(^{\circ}\) (d. h. 1/4 von 360\(^{\circ}\)). Liegt sie um ½ der Periode zurück, spricht man von einem Rückstand von 180\(^{\circ}\) (d. h., sie liegt zeitlich um 1/2 Zyklus zurück). Man kann dies auch so ausdrücken, dass vorlaufende Wellenformen zeitlich früher beginnen und daher links von der Referenz gezeichnet werden, während nachlaufende Wellenformen zeitlich später beginnen und rechts gezeichnet werden.
Abbildung \(\PageIndex{6}\) veranschaulicht die Wirkung der Phasenverschiebung. Beachten Sie, dass in dieser Darstellung \(t = 0\) in die Mitte der horizontalen Achse verschoben wurde. Die mittlere Kurve ist die Ausgangs- oder Referenzwelle (grün). Links (rot) befindet sich eine Welle, die der Ausgangswelle um einen Achtelzyklus vorausläuft, also 45\(^{\circ}\). Rechts (blau) befindet sich eine um die Hälfte nacheilende Welle, d. h. -22,5\(^{\circ}\).
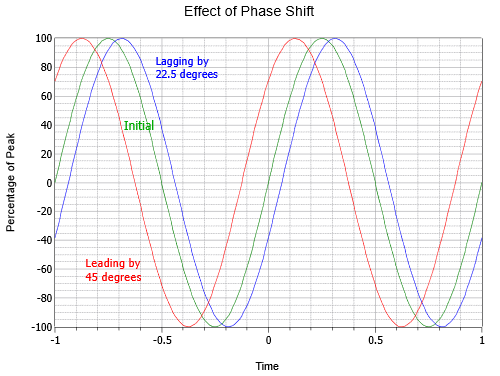
Abbildung \(\PageIndex{6}\): Sinuswellen-Phasenverlauf.
Durch die Kombination der vorgenannten Elemente lässt sich ein allgemeines Format für eine Sinuswelle (Spannung dargestellt) entwickeln:
\
Wobei
\(v(t)\) die Spannung zu einem bestimmten Zeitpunkt \(t\) ist,
\(V_{DC}\) ist der Gleichstromversatz, falls vorhanden,
\(V_{P}\) ist der Spitzenwert,
\(f\) ist die Frequenz,
\(\theta\) ist die Phasenverschiebung (+ wenn voreilend und nach links gezeichnet, – wenn nacheilend und nach rechts gezeichnet).
Als schnelles und praktisches Beispiel hat die in Abbildung \(\PageIndex{4}\) dargestellte Wellenform eine Amplitude von 4 Volt Spitze, eine Frequenz von 5 Hz und keine Gleichstromverschiebung oder Phasenverschiebung. Der Ausdruck lautet also \(v(t) = 4 \sin (2 \pi 5 t)\)
Um eine Phasenverschiebung zu berechnen, bestimmen Sie zunächst die Zeitdifferenz zwischen der Wellenform und der Referenz, die wir \(\Delta t\) nennen. Die Referenz kann ein fester Zeitpunkt (z. B. \(t = 0\)) oder eine andere Wellenform sein. Im Allgemeinen ist es am einfachsten, die Differenz bei den Nulldurchgängen zu messen, vorausgesetzt, es gibt keinen DC-Offset. Liegt eine Verschiebung vor, so ist die Messung an der Stelle vorzunehmen, an die der Nulldurchgang verschoben wurde (d. h. auf dem Niveau der Gleichstromverschiebung). Sobald die Differenz gefunden ist, teilen Sie sie durch die Periode, um die Verschiebung als Bruchteil einer Periode darzustellen. Da ein Zyklus einer Umdrehung des Vektors oder 360 Grad entspricht, multiplizieren Sie den Bruchteil einfach mit 360 Grad, um die Phasenverschiebung in Grad zu ermitteln. Als Formel ausgedrückt:
\
Denken Sie daran, dass eine nach links verschobene Welle vorauseilend und positiv ist, während eine nach rechts verschobene Welle nacheilt oder zeitlich verzögert und somit negativ ist.
Beispiel \(\PageIndex{1}\)
Schreiben Sie den Ausdruck für die in Abbildung \(\PageIndex{7}\) dargestellte Wellenform.
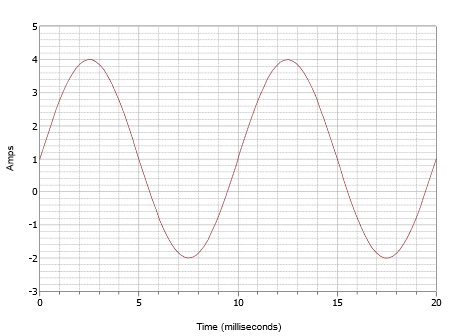
Abbildung \(\PageIndex{7}\): Wellenform für Beispiel \(\PageIndex{1}\).
Diese Wellenform mag oberflächlich betrachtet wie die in Abbildung \(\PageIndex{4}\) aussehen, aber lassen Sie sich davon nicht täuschen. Zunächst einmal ist die Zeitskala anders. Bei dieser Wellenform wird ein Zyklus in 10 Millisekunden abgeschlossen. Daher ist die Frequenz
\
\
\
Das zweite Problem ist der Gleichstromversatz. Man beachte, dass die positive Spitze bei 4 Ampere auftritt, während die negative Spitze bei -2 Ampere auftritt. Daraus ergibt sich ein Spitzenwert von 6 Ampere. Ohne Offset würde die positive Spitze bei 3 Ampere liegen, daher gibt es einen DC-Offset von +1 Ampere. Die vertikale Mitte der Wellenform ist von 0 Ampere auf +1 Ampere nach oben verschoben. Dieser Punkt liegt bei t = 0, daher gibt es keine Phasenverschiebung. Der resultierende Ausdruck lautet:
\
Beispiel \(\PageIndex{2}\)
Schreiben Sie den Ausdruck für die in Abbildung \(\PageIndex{8}\) dargestellte Wellenform.
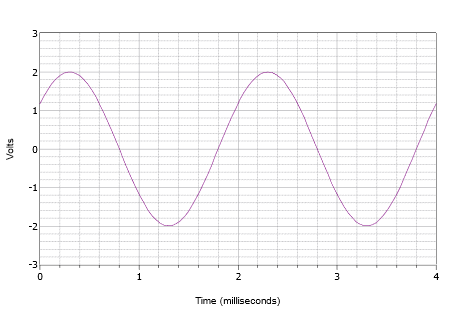
Abbildung \(\PageIndex{8}\): Wellenform für Beispiel \(\PageIndex{2}\).
Zunächst einmal beträgt die positive Spitze 2 Volt und der Spitze-Spitze-Wert 4 Volt. Daher gibt es keinen Gleichstromversatz. Die vertikale Mitte der Welle beginnt nicht bei \(t = 0\), also muss es eine Phasenverschiebung geben. Der Wert bei \(t = 0\) beträgt 1,2 Volt. Die Welle erreicht dieselbe Amplitude bei \(t = 2\) Millisekunden und beginnt, einen weiteren Zyklus zu wiederholen. Folglich muss die Periode 2 Millisekunden betragen. Die Frequenz ist der Kehrwert dieses Wertes, also \(f = 500\) Hz.
Die Wellenform ist nach links verschoben, was eine positive oder vorlaufende Phasenverschiebung anzeigt. Wenn wir den zweiten Zyklus untersuchen, sehen wir, dass er bei 1,8 Millisekunden auf null Volt trifft. Daher beträgt die Verschiebung 0,2 Millisekunden. In Grad ausgedrückt bedeutet dies:
\
\
\
Der endgültige Ausdruck lautet:
\
Beispiel \(\PageIndex{3}\)
Zeichnen Sie die dem folgenden Ausdruck entsprechende Wellenform.
\
Zunächst ist zu beachten, dass der -3-Volt-Versatz die positive Spitze von 5 Volt auf 2 Volt und die negative Spitze von -5 Volt auf -8 Volt drückt. Die Frequenz von 40 kHz ergibt eine Periode von:
\
\
\
Die Phasenverschiebung von -72\(^{\circ}\) entspricht 72/360, also 0,2 Zyklen. Dies entspricht einer (nach rechts verschobenen, weil negativen) Zeitverzögerung von 0,2 mal 25 \(\mu\)s oder 5 \(\mu\)s.
Anfänglich ist es oft am besten, das Diagramm in einer Reihe von diskreten Schritten zu erstellen, anstatt zu versuchen, das Ganze in einem Zug zu zeichnen. Zeichnen Sie zunächst eine Sinuswelle mit einer Spitzenamplitude von 5 Volt und einer Periode von 25 \(\mu\)s. Verschieben Sie nun die Wellenform um 3 Volt nach unten, so dass die positive Spitze nur noch 2 Volt beträgt und die negative Spitze bei -8 Volt liegt. Schieben Sie schließlich die neu verschobene Wellenform um 5 \(\mu\)s nach rechts. Das Ergebnis ist in Abbildung \(\PageIndex{9}\) dargestellt.
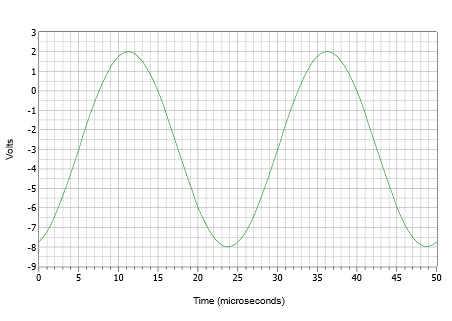
Abbildung \(\PageIndex{9}\): Wellenform für Beispiel \(\PageIndex{3}\).
1.2.1: Labormessungen
Im Labor wird ein Funktionsgenerator verwendet, um Sinus- und andere Wellenformen zu erzeugen. Mit diesen Geräten lassen sich sowohl die Amplitude als auch die Frequenz der Welle genau steuern und, falls gewünscht, ein Gleichstrom-Offset hinzufügen. Ein Beispiel ist in Abbildung \(\PageIndex{10}\) dargestellt. Das entsprechende Messinstrument ist das Oszilloskop, kurz Scope genannt.

Abbildung \(\PageIndex{10}\): Laborsignalgenerator.
Das Oszilloskop ist vielleicht das nützlichste und vielseitigste Messgerät im Labor. In der Regel verfügen sie über zwei oder vier Eingangskanäle, aber auch mehr sind möglich. Jeder Eingangskanal hat seine eigene Empfindlichkeitseinstellung und alle Kanäle haben eine gemeinsame Zeitreferenz. Die Anzeige zeichnet Wellenformen in der gleichen Weise wie in den Abbildungen \(\PageIndex{1}\) – \(\PageIndex{9}\). Außerdem können sie eine Spannung gegen eine andere auftragen (X-Y-Modus). Moderne Oszilloskope verfügen über zusätzliche Funktionen wie die automatische Messung von Frequenz, Amplitude, Phasenverschiebung usw., Cursor-basierte Messungen und die Möglichkeit, Anzeigebilder als Grafikdateien zu speichern. Ein Beispiel für ein digitales Oszilloskop mit vier Kanälen ist in Abbildung \(\PageIndex{11}\) dargestellt.

Abbildung \(\PageIndex{11}\): Ein digitales Oszilloskop.
1.2.2: Schaltplansymbole
Im Schaltplan sind die Symbole für Wechselspannungs- und Stromquellen in Abbildung \(\PageIndex{12}\) dargestellt. Die Polaritäts- und Richtungsmarkierungen sind nicht absolut; schließlich handelt es sich um Wechselstromquellen, deren Polarität und Richtungen sich hin und her bewegen. Die Markierungen dienen vielmehr dazu, einen zeitlichen Bezug herzustellen, insbesondere in Schaltungen, die mehrere Quellen verwenden.
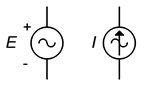
Abbildung \(\PageIndex{12}\): Schematische Symbole für eine Wechselspannungsquelle (links) und eine Stromquelle (rechts).
Es sei daran erinnert, dass das Negieren einer Quelle dasselbe ist wie das Umkehren ihrer Polarität. Dies galt für Gleichstromquellen und gilt auch für Wechselstromquellen. Dies ist in Abbildung \(\PageIndex{13}\) dargestellt. Manchmal macht das Umdrehen oder Negieren der Quelle die Analyse etwas offensichtlicher oder einfacher zu visualisieren.
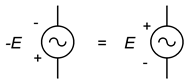
Abbildung \(\PageIndex{13}\): Polarität/Vorzeichen-Äquivalenz.
Beispiel \(\PageIndex{4}\)
Angenommen, ein Oszilloskop zeigt zwei Wellen an, wie sie in Abbildung \(\PageIndex{14}\) dargestellt sind. Bestimmen Sie die Phasenverschiebung der kleineren 20-Volt-Spitzenwert-Wellenform (blau) relativ zur größeren 25-Volt-Spitzenwert-Wellenform (rot).
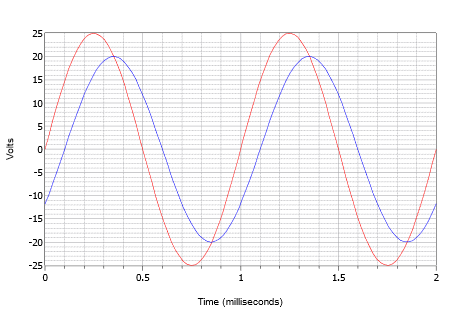
Abbildung \(\PageIndex{14}\): Wellenformen für Beispiel \(\PageIndex{4}\).
Zunächst ist festzustellen, dass keine der beiden Wellen einen Gleichstromversatz aufweist. Wenn eine oder beide Wellen einen Offset hätten, müssten die Wellen vertikal verschoben werden, damit ihre normalen Nulldurchgangspunkte auf gleicher Höhe liegen. Misst man beide Wellen, so ergibt sich eine Periode von 1 Millisekunde. Die Zeitverschiebung lässt sich am einfachsten an einem der Nulldurchgänge feststellen (es stehen vier Stellen zur Auswahl). Die Verzögerung beträgt eine kleine Abweichung oder 0,1 Millisekunden, wobei die kleinere Welle zeitlich verzögert ist oder der größeren Welle hinterherhinkt. Dies zeigt eine negative Phasenverschiebung an.
\
\
\
1.2.3: Sinus und Kosinus
Es gibt eine Handvoll spezieller Phasenverschiebungen, die eine genauere Betrachtung wert sind. Wird eine Sinuskurve invertiert, d.h. auf den Kopf gestellt, ist sie von einer um +180 oder -180 Grad verschobenen Sinuskurve nicht zu unterscheiden. Mit anderen Worten: Eine solche Welle kann auf drei verschiedene Arten geschrieben werden: \(- \sin (2 \pi ft)\), \(\sin (2 \pi ft – 180^{\circ})\), oder \(\sin (2 \pi ft + 180^{\circ})\). Wenn eine Sinuswelle um +90 Grad verschoben ist (d. h. nach vorne und nach links), kann sie auch als Kosinuswelle bezeichnet werden. Somit ist \(\sin (2 \pi ft + 90^{\circ}) = \ cos (2 \pi ft)\). Wird eine Sinuswelle um -90 Grad verschoben (d. h. nacheilend und nach rechts), kann sie als negative oder umgekehrte Kosinuswelle bezeichnet werden. Somit ist \(\sin (2 \pi ft – 90^{\circ}) = – \cos (2 \pi ft)\). Die Beziehungen dieser vier Wellen sind in Abbildung \(\PageIndex{15}\) dargestellt.
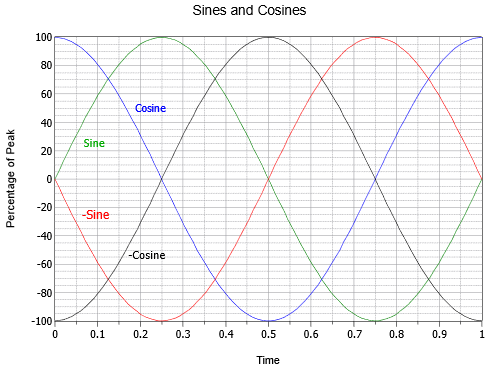
Abbildung \(\PageIndex{15}\): Zeitliche Beziehungen zwischen Sinus und Kosinus.
Es ist auch erwähnenswert, dass die Kosinuswelle die erste Ableitung oder Steigung der Sinuswelle darstellt. Wie Sie sich vielleicht aus anderen Studien erinnern, ist die Steigung oder „Steilheit“ einer Linie das Verhältnis der vertikalen Änderung zur horizontalen Änderung, manchmal auch „Anstieg über dem Verlauf“ genannt. Bei einer Spannung wäre dies die Änderung der Spannung im Verhältnis zur Änderung der Zeit, oder \(\Delta V/ \Delta t\). Bei einer glatten, sich kontinuierlich ändernden Kurve wie einer Sinuswelle ist die Steigung an einem bestimmten Punkt als erste Ableitung definiert, oder in diesem Fall als \(dv/dt\). Um dies visuell zu überprüfen, beachten Sie, dass der steilste Teil der Sinuswelle (grün) dort liegt, wo sie die Nullamplitude durchläuft. Wenn der Sinus den Nulldurchgang bei einer positiven Bewegung durchläuft (bei \(t = 0\) oder \(t = 1\) in Abbildung \(\PageIndex{15}\)), befindet sich der Kosinus (blau) an seiner positiven Spitze. Wenn der Sinus den Nullpunkt durchquert, während er sich negativ bewegt (bei \(t = 0,5\)), hat der Kosinus seine negative Spitze. Außerdem ist die Sinuswelle flach mit einer Steigung von Null an ihrem positiven und negativen Scheitelpunkt (bei \(t = 0,25\) bzw. \(t = 0,75\)), und die Amplitude des Kosinus ist zu diesen Zeitpunkten ebenfalls Null. Es gilt auch, dass die Sinuswelle die Steigung der negativen Kosinuswelle ist, der negative Kosinus die Steigung des negativen Sinus und der negative Sinus die Steigung des Kosinus ist. In umgekehrter Richtung können wir sagen, dass die Anti-Ableitung (unbestimmtes Integral) einer Kosinuswelle eine Sinuswelle ist, das Integral einer Sinuswelle eine negative Kosinuswelle ist und so weiter. Diese Beziehungen werden sich als sehr nützlich erweisen, wenn wir uns mit dem Verhalten von Kondensatoren und Induktoren in Wechselstromkreisen befassen.
1.2.4: RMS – Root Mean Square Measurement
Neben dem Spitzenwert und dem Spitze-Spitze-Wert kann die Amplitude auch als RMS-Wert (Root Mean Square) angegeben werden. Wenn kein Spitzenwert oder Spitze-Spitze-Wert angegeben wird, wird davon ausgegangen, dass die Messung als RMS-Wert erfolgt. RMS ist eine spezielle Berechnung, die zur Ermittlung der äquivalenten Gleichstromleistung verwendet wird (z. B. sehr häufig bei Audio-Leistungsverstärkern). Mit anderen Worten, wenn wir die Leistung in einem Widerstand ermitteln wollen, muss die Berechnung mit RMS-Werten für Spannung oder Strom durchgeführt werden, nicht mit Spitzenwerten oder Spitze-Spitze-Werten. Andernfalls ergeben sich falsche Leistungen. Dies gilt unabhängig von der Wellenform, sei es eine Sinuswelle, eine Dreieckswelle oder die komplexen Wellen von Musiksignalen. Wenn eine Spannung als Effektivwert angegeben wird, kann sie für Leistungsberechnungen genauso behandelt werden wie eine gleich große Gleichspannung. Ein Sinus mit einem Effektivwert von 1 Volt erzeugt zum Beispiel die gleiche Verlustleistung und Erwärmung in einem bestimmten Widerstand wie 1 Volt Gleichspannung. Aus diesem Grund wird der Effektivwert manchmal auch als Effektivwert (d. h. effektiver Gleichstromwert) bezeichnet.
Der Name Effektivwert beschreibt den Prozess der Bestimmung des Effektivwerts. Zunächst sei daran erinnert, dass die Leistung proportional zum Quadrat der Spannung oder des Stroms ist. Unser erster Schritt besteht also darin, die Eingangswellenform zu quadrieren. Natürlich ist die Wellenform eine Funktion der Zeit, und ihr Quadrat wird eine neue Form ergeben. An diesem Punkt müssen wir den Mittelwert dieser neuen Form finden. Der Grund dafür ist einfach, aber nicht unbedingt offensichtlich. Elektrische und elektronische Bauteile haben eine Masse und erwärmen oder kühlen sich daher nicht sofort. Sie weisen eine thermische Zeitkonstante auf. Daher reagieren sie auf den durchschnittlichen Input über die Zeit. Wir könnten zwar eine Art „momentane Spitzenleistung“ zu einem bestimmten Zeitpunkt berechnen, aber das entspricht nicht der entsprechenden Gleichstromleistung. Sobald wir den Mittelwert dieser quadrierten Wellenform erhalten haben, ist der entsprechende Gleichstromwert einfach die Quadratwurzel aus dem Mittelwert. Das Ergebnis ist ein gebrochener Wert zwischen Null und Eins, der als Skalierungsfaktor verwendet wird, um einen Spitzenwert in einen Effektivwert umzuwandeln. Der Wert ist für die jeweilige Wellenform eindeutig. Das heißt, alle Sinuswellen (unabhängig von der Phase) haben denselben Faktor, alle regelmäßigen Dreieckswellen haben denselben Faktor usw. Da wir uns hauptsächlich mit Sinuswellen beschäftigen, wollen wir uns die Bestimmung des RMS-Faktors für diese Wellenform genauer ansehen.
Wir beginnen mit dem grundlegenden Ausdruck für eine Sinuswelle ohne Gleichstromversatz oder Phasenverschiebung und mit einer Amplitude von eins:
\
Der erste Schritt besteht darin, diese Wellenform zu quadrieren. Eine nützliche trigonometrische Identität ist
\
Wenn man dies auf unsere Welle anwendet, erhält man:
\
Dieser Ausdruck beschreibt eine umgekehrte Kosinuswelle mit der doppelten ursprünglichen Frequenz und der Hälfte der ursprünglichen Amplitude, die auf einer Gleichstromverschiebung reitet, die ihrem Spitzenwert entspricht. Mit anderen Worten, die negative Spitze des Kosinus liegt bei Null und die positive Spitze bei 1. Der nächste Schritt besteht darin, den Mittelwert dieses Zwischenergebnisses zu ermitteln. Der Mittelwert ist gleich dem Offset von 0,5. Man kann sich das so vorstellen, dass der Bereich oberhalb des Offsets die „Senke“ unterhalb des Offsets perfekt ausfüllt. Der letzte Schritt besteht darin, die Quadratwurzel aus dem Mittelwert zu ziehen. Die Quadratwurzel aus 0,5 ist gleich eins über der Quadratwurzel aus zwei, also ungefähr 0,707. Der RMS-Wert ist also das 0,707-fache des Spitzenwertes. Alternativ können Sie den Spitzenwert durch die Quadratwurzel aus zwei teilen, was ungefähr 1,414 entspricht. Dieses Verfahren ist in Abbildung \(\PageIndex{16}\) grafisch dargestellt.
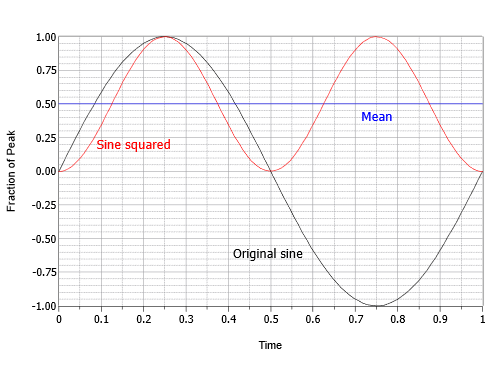
Abbildung \(\PageIndex{16}\): Verfahren zur Ermittlung des RMS-Faktors für Sinuswellen.
Bei Sinuswellen ist der RMS immer der Spitzenwert mal 0,707. Man könnte auch sagen, der RMS-Wert einer Sinuswelle ist ihr Spitzenwert geteilt durch etwa 1,414. Auch hier gilt, dass diese Verhältnisse nicht notwendigerweise für nicht-sinusförmige Wellen gelten. Einzelheiten zu anderen gängigen Formen finden Sie in Anhang C. Schließlich wird das Verhältnis zwischen dem Spitzenwert und dem Effektivwert als Scheitelwertverhältnis bezeichnet. Dies ist ein fester Wert für Sinuswellen (wiederum etwa 1,414), kann aber bei einigen Arten von Audiosignalen über 10:1 liegen.
1.2.5: Wellenlänge
Ein weiterer Punkt von Interesse ist die Ausbreitungsgeschwindigkeit der Welle. Diese variiert stark. Im Falle von Licht im Vakuum (oder, in guter Näherung, eines elektrischen Stroms in einem Draht) beträgt die Geschwindigkeit etwa 3E8 Meter pro Sekunde (d.h. 300.000 km/s) oder etwa 186.000 Meilen pro Sekunde.
Angesichts einer Geschwindigkeit und einer Periode können wir uns vorstellen, wie weit die Spitzen der Welle voneinander entfernt sind. Dieser Abstand wird Wellenlänge genannt und mit dem griechischen Buchstaben Lambda \(\lambda\) bezeichnet. Die Wellenlänge ist gleich der Geschwindigkeit geteilt durch die Frequenz, \(\lambda = v/f\). Bei einem Lautsprecher, der einen Sinus von 100 Hz erzeugt, beträgt die Schallgeschwindigkeit in der Luft 344 m/s, also \(\lambda = 344 m/s \, / \, 100\) Hz, oder 3,44 Meter (etwas über 11 Fuß). Je höher die Frequenz, desto kürzer die Wellenlänge. Außerdem gilt: Je höher die Geschwindigkeit, desto länger die Wellenlänge. Wellenlängenberechnungen sind in den Bereichen Telekommunikation und Akustik von besonderer Bedeutung.