Bindungsstärke: Kovalente Bindungen
Stabile Moleküle existieren, weil kovalente Bindungen die Atome zusammenhalten. Die Stärke einer kovalenten Bindung wird anhand der Energie gemessen, die erforderlich ist, um sie zu brechen, d. h. die Energie, die erforderlich ist, um die gebundenen Atome zu trennen. Die Trennung eines beliebigen Paares gebundener Atome erfordert Energie; je stärker eine Bindung ist, desto größer ist die Energie, die zum Brechen der Bindung erforderlich ist. Die Energie, die zum Aufbrechen einer bestimmten kovalenten Bindung in einem Mol gasförmiger Moleküle erforderlich ist, wird als Bindungsenergie oder Bindungsdissoziationsenergie bezeichnet. Die Bindungsenergie für ein zweiatomiges Molekül, \(D_{X-Y}\), ist definiert als die Standard-Enthalpieänderung für die endotherme Reaktion:
\
Zum Beispiel beträgt die Bindungsenergie der reinen kovalenten H-H-Bindung, \(\Delta_{H-H}\), 436 kJ pro Mol gebrochener H-H-Bindungen:
\
Beim Brechen einer Bindung muss dem Molekül immer Energie zugeführt werden. Dementsprechend wird beim Schließen einer Bindung immer Energie freigesetzt.
Moleküle mit drei oder mehr Atomen haben zwei oder mehr Bindungen. Die Summe aller Bindungsenergien in einem solchen Molekül ist gleich der Standard-Enthalpieänderung für die endotherme Reaktion, die alle Bindungen im Molekül bricht. Zum Beispiel ist die Summe der vier C-H-Bindungsenergien in CH4, 1660 kJ, gleich der Standard-Enthalpieänderung der Reaktion:
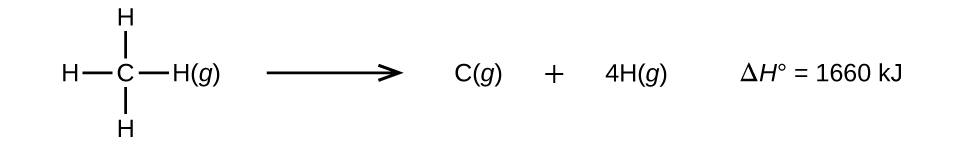
Die durchschnittliche C-H-Bindungsenergie, \(D_{C-H}\), beträgt 1660/4 = 415 kJ/mol, da vier Mol C-H-Bindungen pro Mol der Reaktion gebrochen werden. Obwohl die vier C-H-Bindungen im ursprünglichen Molekül äquivalent sind, benötigen sie nicht alle die gleiche Energie zum Brechen; sobald die erste Bindung gebrochen ist (wofür 439 kJ/mol erforderlich sind), sind die übrigen Bindungen leichter zu brechen. Der Wert von 415 kJ/mol ist ein Durchschnittswert, nicht der genaue Wert, der zum Brechen einer Bindung erforderlich ist.
Die Stärke einer Bindung zwischen zwei Atomen nimmt mit der Anzahl der Elektronenpaare in der Bindung zu. Im Allgemeinen nimmt mit zunehmender Bindungsstärke die Bindungslänge ab. So sind Dreifachbindungen stärker und kürzer als Doppelbindungen zwischen denselben beiden Atomen; ebenso sind Doppelbindungen stärker und kürzer als Einfachbindungen zwischen denselben beiden Atomen. Die durchschnittlichen Bindungsenergien für einige häufige Bindungen sind in Tabelle \(\PageIndex{2}\) aufgeführt, und ein Vergleich der Bindungslängen und Bindungsstärken für einige häufige Bindungen findet sich in Tabelle \(\PageIndex{2}\). Wenn sich ein Atom an verschiedene Atome in einer Gruppe bindet, nimmt die Bindungsstärke in der Regel ab, je weiter man sich in der Gruppe nach unten bewegt. Zum Beispiel beträgt C-F 439 kJ/mol, C-Cl 330 kJ/mol und C-Br 275 kJ/mol.
| Bindung | Bindungsenergie | Bindung | Bindungsenergie | Bindung | Bindungsenergie | ||
|---|---|---|---|---|---|---|---|
| H-H | 436 | C-S | 260 | F-Cl | 255 | ||
| H-C | 415 | C-Cl | 330 | F-Br | 235 | ||
| H-N | 390 | C-Br | 275 | Si-Si | 230 | ||
| H-O | 464 | C-I | 240 | Si-P | 215 | ||
| H-F | 569 | N-N | 160 | Si-S | 225 | ||
| H-Si | 395 | \(\mathrm{N=N}\) | 418 | Si-Cl | 359 | ||
| H-P | 320 | \(\mathrm{N≡N}\) | 946 | Si-Br | 290 | ||
| H-S | 340 | N-O | 200 | Si-I | 215 | ||
| H-Cl | 432 | N-F | 270 | P-P | 215 | ||
| H-Br | 370 | N-P | 210 | P-S | 230 | ||
| H-I | 295 | N-Cl | 200 | P-Cl | 330 | ||
| C-C | 345 | N-Br | 245 | P-Br | 270 | ||
| \(\mathrm{C=C}\) | 611 | O-O | 140 | P-I | 215 | ||
| \(\mathrm{C≡C}\) | 837 | \(\mathrm{O=O}\) | 498 | S-S | 215 | ||
| C-N | 290 | O-F | 160 | S-Cl | 250 | ||
| \(\mathrm{C=N}\) | 615 | O-Si | 370 | S-Br | 215 | ||
| \(\mathrm{C≡N}\) | 891 | O-P | 350 | Cl-Cl | 243 | ||
| C-O | 350 | O-Cl | 205 | Cl-Br | 220 | ||
| \(\mathrm{C=O}\) | 741 | O-I | 200 | Cl-I | 210 | ||
| \(\mathrm{C≡O}\) | 1080 | F-F | 160 | Br-Br | 190 | ||
| C-F | 439 | F-Si | 540 | Br-I | 180 | ||
| C-Si | 360 | F-P | 489 | I-I | 150 | ||
| C-P | 265 | F-S | 285 |
| Bindung | Bindungslänge (Å) | Bindungsenergie (kJ/mol) |
|---|---|---|
| C-C | 1.54 | 345 |
| \(\mathrm{C=C}\) | 1.34 | 611 |
| \(\mathrm{C≡C}\) | 1.20 | 837 |
| C-N | 1.43 | 290 |
| \(\mathrm{C=N}\) | 1.38 | 615 |
| \(\mathrm{C≡N}\) | 1.16 | 891 |
| C-O | 1.43 | 350 |
| \(\mathrm{C=O}\) | 1.23 | 741 |
| \(\mathrm{C≡O}\) | 1.13 | 1080 |
Wir können Bindungsenergien verwenden, um ungefähre Enthalpieänderungen für Reaktionen zu berechnen, für die keine Bildungsenthalpien verfügbar sind. Berechnungen dieser Art sagen uns auch, ob eine Reaktion exotherm oder endotherm ist.
- Eine exotherme Reaktion (ΔH negativ, erzeugte Wärme) entsteht, wenn die Bindungen in den Produkten stärker sind als die Bindungen in den Reaktanten.
- Eine endotherme Reaktion (ΔH positiv, absorbierte Wärme) entsteht, wenn die Bindungen in den Produkten schwächer sind als die in den Reaktanten.
Die Enthalpieänderung, ΔH, für eine chemische Reaktion ist ungefähr gleich der Summe der Energie, die benötigt wird, um alle Bindungen in den Reaktanten zu brechen (Energie „in“, positives Vorzeichen) plus der Energie, die freigesetzt wird, wenn alle Bindungen in den Produkten gebildet werden (Energie „out“, negatives Vorzeichen). Dies lässt sich mathematisch folgendermaßen ausdrücken:
\
In diesem Ausdruck bedeutet das Symbol \(\Sigma\) „die Summe von“ und D steht für die Bindungsenergie in Kilojoule pro Mol, die immer eine positive Zahl ist. Die Bindungsenergie wird aus einer Tabelle entnommen und hängt davon ab, ob es sich bei der jeweiligen Bindung um eine Einfach-, Doppel- oder Dreifachbindung handelt. Bei der Berechnung von Enthalpien auf diese Weise ist es daher wichtig, dass wir die Bindungen in allen Reaktanten und Produkten berücksichtigen. Da es sich bei den D-Werten in der Regel um Durchschnittswerte für einen Bindungstyp in vielen verschiedenen Molekülen handelt, liefert diese Berechnung eine grobe Schätzung und keinen exakten Wert für die Reaktionsenthalpie.
Betrachten Sie die folgende Reaktion:
oder
\
Um zwei Mole HCl zu bilden, müssen ein Mol H-H-Bindungen und ein Mol Cl-Cl-Bindungen gebrochen werden. Die zum Brechen dieser Bindungen erforderliche Energie ist die Summe der Bindungsenergie der H-H-Bindung (436 kJ/mol) und der Cl-Cl-Bindung (243 kJ/mol). Während der Reaktion werden zwei Mole von H-Cl-Bindungen gebildet (Bindungsenergie = 432 kJ/mol), wodurch 2 × 432 kJ oder 864 kJ freigesetzt werden. Da die Bindungen in den Produkten stärker sind als die in den Reaktanten, wird bei der Reaktion mehr Energie freigesetzt als verbraucht:
\-2D_{H-Cl}}\
&=\mathrm{-2(432)=-185\:kJ}
\end {align*}\]
Diese überschüssige Energie wird als Wärme freigesetzt, so dass die Reaktion exotherm ist. Tabelle T2 gibt einen Wert für die molare Standardbildungsenthalpie von HCl(g), \(ΔH^\circ_\ce f\), von -92,307 kJ/mol an. Das Doppelte dieses Wertes ist -184,6 kJ, was gut mit der zuvor erhaltenen Antwort für die Bildung von zwei Molen HCl übereinstimmt.
Beispiel \(\PageIndex{1}\): Verwendung von Bindungsenergien zur Annäherung an Enthalpieänderungen
Methanol, CH3OH, kann ein ausgezeichneter alternativer Kraftstoff sein. Bei der Hochtemperaturreaktion von Wasserdampf und Kohlenstoff entsteht ein Gemisch aus den Gasen Kohlenmonoxid (CO) und Wasserstoff (H2), aus dem Methanol hergestellt werden kann. Berechnen Sie anhand der Bindungsenergien in Tabelle \(\PageIndex{2}\) die ungefähre Enthalpieänderung, ΔH, für die folgende Reaktion:
\
Lösung
Zunächst müssen wir die Lewis-Strukturen der Reaktanten und der Produkte schreiben:
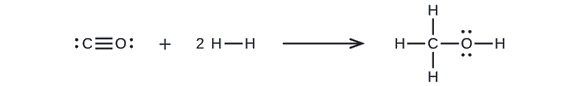
Daraus geht hervor, dass ΔH für diese Reaktion die Energie umfasst, die erforderlich ist, um eine C-O-Dreifachbindung und zwei H-H-Einfachbindungen zu brechen, sowie die Energie, die durch die Bildung von drei C-H-Einfachbindungen, einer C-O-Einfachbindung und einer O-H-Einfachbindung entsteht. Wir können dies wie folgt ausdrücken (über Gleichung \ref{EQ3}):
\-}
\end {align*}\]
Unter Verwendung der Bindungsenergiewerte in Tabelle \(\PageIndex{2}\) erhalten wir:
&=\ce{-107\:kJ}
\end {align*}\]
Wir können diesen Wert mit dem Wert vergleichen, der anhand der \(ΔH^\circ_\ce f\)-Daten aus Anhang G berechnet wurde:
&=-\\
&=\mathrm{-90.5\:kJ}
\end {align*}\]
Beachten Sie, dass zwischen den mit den beiden verschiedenen Methoden berechneten Werten eine ziemlich große Lücke besteht. Dies liegt daran, dass die D-Werte der Durchschnitt verschiedener Bindungsstärken sind und daher oft nur grob mit anderen Daten übereinstimmen.
Übung \(\PageIndex{1}\)
Ethylalkohol, CH3CH2OH, war eine der ersten organischen Chemikalien, die vom Menschen bewusst synthetisiert wurden. Er wird in der Industrie vielfach verwendet und ist der in alkoholischen Getränken enthaltene Alkohol. Er kann durch die Fermentation von Zucker gewonnen oder durch die Hydratation von Ethylen in der folgenden Reaktion synthetisiert werden:

Berechnen Sie unter Verwendung der Bindungsenergien in Tabelle \(\PageIndex{2}\) eine ungefähre Enthalpieänderung ΔH für diese Reaktion.
Zusammenfassung
Video \(\PageIndex{2}\): Ein Überblick über die atomare Bindung.
Kovalente Bindungen entstehen, wenn Elektronen zwischen Atomen geteilt werden und von den Kernen beider Atome angezogen werden. Bei reinen kovalenten Bindungen sind die Elektronen gleichmäßig verteilt. Bei polaren kovalenten Bindungen sind die Elektronen ungleich verteilt, da ein Atom eine stärkere Anziehungskraft auf die Elektronen ausübt als das andere.
Die Stärke einer kovalenten Bindung wird anhand ihrer Bindungsdissoziationsenergie gemessen, d. h. der Energiemenge, die erforderlich ist, um diese bestimmte Bindung in einem Molekül zu brechen. Mehrfachbindungen sind stärker als Einfachbindungen zwischen denselben Atomen. Die Enthalpie einer Reaktion kann auf der Grundlage der zum Brechen von Bindungen erforderlichen Energie und der bei der Bildung neuer Bindungen freigesetzten Energie geschätzt werden.
Schlüsselgleichungen
- Bindungsenergie für ein zweiatomiges Molekül: \(\ce{XY}(g)⟶\ce{X}(g)+\ce{Y}(g)\hspace{20px}\ce{D_{X–Y}}=ΔH°\)
- Enthalpy change: ΔH = ƩBindungen gebrochen – ƩBindungen gebildet
Footnotes
- Diese Frage stammt aus der Chemistry Advanced Placement Examination und wird mit Genehmigung des Educational Testing Service verwendet.
Glossar
Bindungsenergie (auch Bindungsdissoziationsenergie) Energie, die erforderlich ist, um eine kovalente Bindung in einer gasförmigen Substanz zu brechen
Autoren
-
Paul Flowers (University of North Carolina – Pembroke), Klaus Theopold (University of Delaware) und Richard Langley (Stephen F. Austin State University) mit beitragenden Autoren. Die von OpenStax College produzierten Lehrbuchinhalte sind unter einer Creative Commons Attribution License 4.0 Lizenz lizenziert. Kostenloser Download unter http://cnx.org/contents/85abf193-2bd…[email protected]).
- Adelaide Clark, Oregon Institute of Technology
- Fuse School, Open Educational Resource free of charge, under a Creative Commons License: Attribution-NonCommercial CC BY-NC (View License Deed: https://creativecommons.org/licenses/by-nc/4.0/)
- Crash Course Chemistry: Crash Course ist eine Abteilung von Complexly und die Videos können zu Bildungszwecken kostenlos gestreamt werden.
Feedback
Sie haben ein Feedback zu diesem Text zu geben? Klicken Sie hier.
Sie haben einen Tippfehler gefunden und möchten eine zusätzliche Note? Klicken Sie hier.