Einführung
Koordinatentransformationen sind in 2-D nicht intuitiv genug und in 3-D äußerst schmerzhaft. Auf dieser Seite werden sie in der folgenden Reihenfolge behandelt: (i) Vektoren in 2-D, (ii) Tensoren in 2-D, (iii) Vektoren in 3-D, (iv) Tensoren in 3-D und schließlich (v) Tensortransformationen vierten Ranges.
Ein wichtiger Aspekt der Koordinatentransformationen ist die Auswertung der Transformationsmatrix, insbesondere in 3-D. Es ist sehr wichtig zu erkennen, dass alle Koordinatentransformationen auf dieser Seite Rotationen des Koordinatensystems sind, während das Objekt selbst fest bleibt. Das „Objekt“ kann ein Vektor wie Kraft oder Geschwindigkeit oder ein Tensor wie Spannung oder Dehnung in einer Komponente sein. Objektdrehungen werden in späteren Abschnitten behandelt.
2-D-Koordinatentransformationen von Vektoren
Die akademische Kartoffel liefert ein hervorragendes Beispiel dafür, wie Koordinatentransformationen auf Vektoren angewendet werden, wobei gleichzeitig betont wird, dass es das Koordinatensystem ist, das sich dreht, und nicht der Vektor… oder die Kartoffel.
Die Kartoffel auf der linken Seite hat einen Vektor. Daher wurde der Kartoffel ein Koordinatensystem hinzugefügt, wie rechts dargestellt, so dass der Vektor nun als \({\bf v} = 2{\bf i} + 9{\bf j}\) beschrieben werden kann.

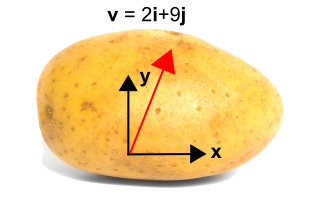
So führen wir nun ein gedrehtes Koordinatensystem ein, das unten in blau dargestellt ist, und verwenden\(x’\) und \(y’\). Das neue System wird gegenüber dem ursprünglichen Koordinatensystem um einen Winkel \(\theta\) gegen den Uhrzeigersinn gedreht. Dabei ist zu beachten, dass sich der Vektor selbst überhaupt nicht ändert. Es ist immer noch derselbe Vektor wie zuvor. Aber er wird im neuen Koordinatensystem durch andere Zahlenwerte beschrieben. In diesem Fall liegt der Vektor näher an der neuen \(x’\)-Achse als an der \(y’\)-Achse, so dass die \({\bf i‘}\)-Komponente größer als die \({\bf j‘}\)-Komponente sein wird. Die Transformation ist unter der Abbildung angegeben.
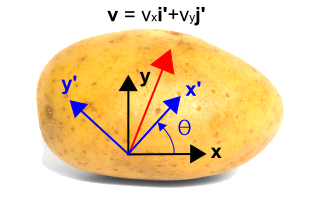
\\
Diese vier Faktoren bilden die vier Terme in den Transformationsgleichungen. Sie lassen sich leicht überprüfen, indem man \(\theta = 0^\circ \) und \(\theta = 90^\circ \) setzt. Wenn \(\theta = 0^\circ \), dann ist \(v’_x = v_x\) und \(v’_y = v_y\). Wenn \(\theta = 90^\circ\), dann \(v’_x = v_y\) und \(v’_y = -v_x\).
Transformationsmatrix
Es ist bequemer, Transformationsgleichungen mit Hilfe von Matrizen zu schreiben (und damit zu arbeiten).
\\links\{ \matrix {v_x \\ v_y}
Die \(\cos \theta\)-Terme befinden sich auf der Matrixdiagonalen, während die \(\sin \theta\)-Terme außerhalb der Diagonalen liegen. Die einzige Schwierigkeit besteht darin, sich zu merken, welcher \(\sin \theta\)-Term das Minuszeichen hat. Es ist immer der linke untere Term.
Die obige Gleichung wird in Matrixschreibweise als
\
geschrieben, wobei \({\bf Q}\) der übliche Buchstabe für die Transformationsmatrix ist.

Transformations- vs. Rotationsmatrizen
Als ob dieses Thema nicht schon schwierig genug wäre, tragen viele Bücher und Webseiten zur Verwirrung bei, indem sie nicht klarstellen, was fest und was rotierend ist. Auf dieser und der nächsten Seite ist es das Koordinatensystem, das sich dreht, während das Objekt fixiert bleibt, weshalb hier der Begriff Transformationsmatrix verwendet wird, um dies zu betonen.
Wir werden uns jedoch später mit Situationen befassen, in denen sich das Objekt dreht, während das Koordinatensystem fixiert bleibt. In diesem Fall wird der Begriff Rotationsmatrix verwendet, um zu betonen, dass sich das Objekt dreht.
Viele Verwirrungen ergeben sich aus der erstaunlichen Tatsache, dass jede Matrix (Transformation und Rotation) nur die Transponierung der anderen ist! Sie sehen sich also extrem ähnlich. Bei 2D-Problemen besteht der einzige praktische Unterschied darin, ob das Minuszeichen vor \(\sin \theta\) auf dem \(q_{12}\)-Term oder dem \(q_{21}\)-Term steht.
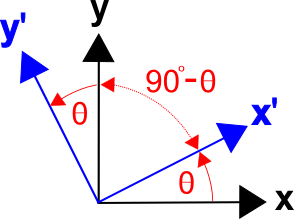
Es gibt eine allgemeine Methode zur Formulierung von Transformationsmatrizen, die auf den Kosinus der Winkel zwischen den Achsen der beiden Koordinatensysteme basiert, d.h. auf den Richtungskosinus. (Dies gilt auch für 3D-Transformationen.)Die Transformationsmatrix kann wie folgt geschrieben werden
\\]
wobei \((x‘,x)\) den Winkel zwischen den Achsen \(x’\) und \(x\) darstellt, \((x‘,y)\) ist der Winkel zwischen den Achsen \(x’\) und \(y\), usw.
Der Winkel zwischen \(x’\) und \(y\) ist \((90^\circ – \theta)\), und \(\cos(x‘,y) = \cos(90^\circ – \theta) = \sin \theta\).
Gleichermaßen ist der Winkel zwischen \(y’\) und \(x\) \((90^\circ + \theta)\), und \(\cos(y‘,x) = \cos(90^\circ + \theta) = -\sin \theta\).
Tensornotation
Die Koordinatentransformation wird in Tensornotation geschrieben als
\
wobei \(\lambda_{ij}\) die Transformationsmatrix \({\bf Q}\) ist. (Ich weiß nicht, warum \({\bf Q}\) in der Matrixschreibweise verwendet wird, aber \(\lambda_{ij}\), nicht \(q_{ij}\), wird in der Tensordarstellung verwendet.) \(\lambda_{ij}\) ist definiert als
\
Wenn zum Beispiel \(i = 1\) und \(j = 2\), dann ist
\
\(\lambda_{ij}\) der Richtungskosinus des Winkels zwischen der \(x’_i\) Achse und der \(x_j\) Achse. Dies gilt auch für 3-D-Transformationen.
2-D-Koordinatentransformationen von Tensoren
In diesem Abschnitt wird das Was und das Wie von Tensortransformationen vorgestellt.
Koordinatentransformationen von Tensoren 2. Ranges beinhalten die gleiche \({\bf Q}\)-Matrix wie Vektortransformationen. Eine Transformation des Spannungstensors, \(\boldsymbol{\sigma}\), vom Referenz-\(x-y\)-Koordinatensystem zu \(\boldsymbol{\sigma‘}\) in ein neues \(x‘-y’\)-System wird wie folgt durchgeführt.
\
Schreibt man die Matrizen explizit aus, so erhält man
\ = \left \left \left \]
(Beachten Sie, dass der Spannungstensor immer symmetrisch ist, auch nach Transformationen.)
Multipliziert man die Matrizen aus, so erhält man
\
Diese drei Gleichungen sind genau die 2D-Transformation eines Spannungstensors, der sich aus der Summierung der Kräfte auf ein Differentialelement und der Auferlegung eines Gleichgewichts ergibt. Dies wird auch durch den Mohrschen Kreis dargestellt.
Tensornotation
Die Koordinatentransformation wird in Tensornotation geschrieben als
\
Wie üblich bietet die Tensornotation einen zusätzlichen Einblick in den Prozess. Diesmal ergibt sich der Einblick aus den Indizes der Lambdas. Jedes Lambda paart ein tiefgestelltes Zeichen auf \(\boldsymbol{\sigma‘}\) mit einem auf \(\boldsymbol{\sigma}\), unabhängig vom Rang des Tensors.
3-D-Koordinatentransformationen von Vektoren
Viele der allgemeinen Gleichungen, die in 2-D-Transformationen verwendet werden, sind auch in 3-D anwendbar.Beispiele sind
\
Nur die Details sind jetzt anders. Die Vektoren haben z-Komponenten und die Transformationsmatrizen sind 3×3 statt 2×2.
\\]
\\]
\ \links\{ \matrix { v_x \\\ v_y \\ v_z } \right\}\]
3-D-Koordinatentransformationen von Tensoren
Auch hier ändern sich die Regeln nicht, nur die Einzelheiten.
\
Wenn man die Matrizen explizit ausschreibt, erhält man
\ = \left\left\left\]
Diese Webseite führt Koordinatentransformationen an 3-D-Tensoren durch. Probieren Sie es aus.
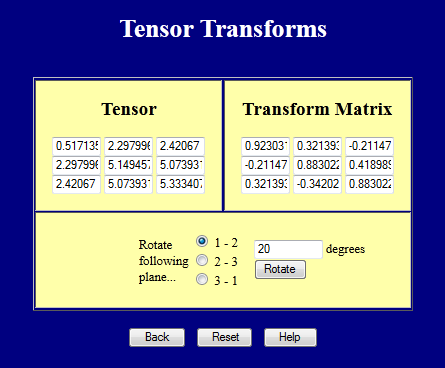
Koordinatentransformationen von Tensoren 4. Ranges
Wir werden im Abschnitt über das Hooke’sche Gesetz sehen, dass der Steifigkeitstensor 4. Rang hat, d.h. 3x3x3x3 (nicht 4×4). Er wird als \(C_{ijkl}\) geschrieben, weil er jede Dehnungskomponente, \(\epsilon_{kl}\), mit jeder Spannungskomponente, \(\sigma_{ij}\), in Beziehung setzt, d.h., \(\sigma_{ij} = C_{ijkl} \epsilon_{kl}\).Das Koordinatentransformationsgesetz für den Steifigkeitstensor 4. Ranges lässt sich leicht in Tensornotation schreiben als
\
Die Tensorgleichung zeigt, wie man die Transformation in Matrixnotation schreibt.
\
Zusammenfassung
Die Koordinatentransformation eines Vektors in Matrix- und Tensornotation ist
\
Die Koordinatentransformation eines Tensors in Matrix- und Tensornotation ist
\
Beachte, dass \({\bf Q}\) und \(\lambda_{ij}\) die gleiche Transformationsmatrix sind.
In 2-D sind \({\bf Q}\) und \(\lambda_{ij}\) definiert als
\\]
, was ein Spezialfall der allgemeineren 3-D-Form ist
\\]