Proportional ist nur eine Möglichkeit, auf einen Fehler im System zu reagieren. Das Problem bei der Proportionalsteuerung ist, dass sie keine Trends erkennen und sich darauf einstellen kann. Dies ist die Aufgabe der Integralsteuerung.
In Abbildung 6 ist links ein weiteres Beispiel für den Fehler in einem System über die Zeit dargestellt. Auch hier könnte es sich um die Entfernung eines Roboters zu einem Objekt handeln, oder um den Flüssigkeitsstand in einem Tank oder die Temperatur in einem Fabrikofen. Vielleicht entfernt sich das Ziel, dem der Roboter folgt, immer weiter vom Roboter, und zwar mit einer Geschwindigkeit, die der Roboter nicht mehr einholen kann. Vielleicht ist die Dichtung der Ofentür verschlissen, vielleicht ist die Flüssigkeitsentnahme aus dem Tank ungewöhnlich hoch. Unabhängig von der Ursache kann die Proportionalsteuerung das Problem nicht erkennen und korrigieren, da sie nicht für die Reaktion auf Trends ausgelegt ist. Hier kommt die Integralsteuerung ins Spiel.
Integral misst den Bereich zwischen den Fehlerwerten und der Zeitachse. Wenn der Fehler nicht auf Null zurückgeht, wird die Fläche des Fehlers immer größer. Die rechte Seite von Abbildung 6 zeigt, wie die Integralausgabe auf diese Art von Trend reagieren kann. Wenn die Fläche zwischen der Fehlerkurve und der Zeitachse zunimmt, steigt der Ausgang proportional zu dieser Fläche. Infolgedessen treibt der Ausgang das Stellglied immer stärker an, um den Fehler zu korrigieren.
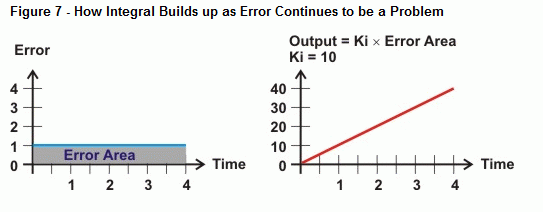
Was passiert nun, wenn der Fehler keine gerade Linie ist, wie die in Abbildung 8 gezeigte Kurve? Das ist es, was die Rechenoperation der Integration bestimmt: die Fläche zwischen einer Kurve und einer Achse. Im Falle der Integralsteuerung wächst die Fläche unter der Kurve, je mehr Zeit mit einer Abweichung vergeht, und damit auch der Wert, den die Integralberechnung verwendet, um gegen den Systemfehler zu steuern. Wenn die Fehlerkurve unter die Zeitachse fällt, wird die Zunahme der negativen Fläche von der Zunahme der positiven Fläche abgezogen. Bei richtiger Einstellung kann die Integralsteuerung dem System helfen, sich auf einen Fehler von Null einzustellen.
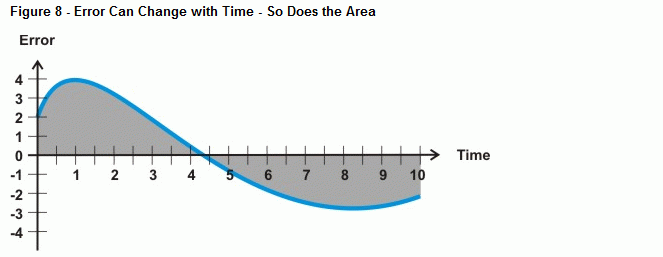
Die BASIC Stamp kann den Fehler unter der Kurve mit numerischer Integration annähern. Abbildung 9 zeigt, wie man den Fehler unter einer Kurve annähern kann, indem man die Fläche einer Reihe von kleinen Rechtecken zwischen der Fehlerkurve und der Zeitachse addiert. Die Fläche jedes Kästchens ist der Fehler multipliziert mit der Zeit zwischen den Messungen. Durch Aufsummieren aller Kästchenflächen erhält man eine Annäherung an die Fläche unter der Kurve.
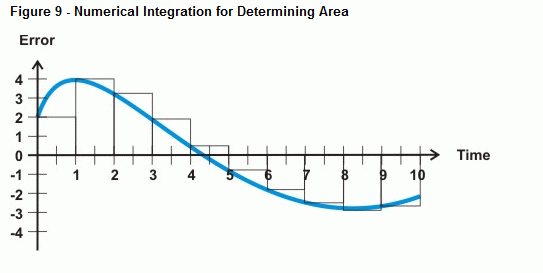
Solange Ihre Messungen gleichmäßig verteilt sind, können Sie die Breite jedes Kästchens mit dem Wert 1 bezeichnen. Das macht die Berechnung viel einfacher, als wenn Sie versuchen, 20 ms zwischen den Messungen, 5 Minuten zwischen den Messungen oder was auch immer Ihre Abtastrate sein mag, zu berücksichtigen. Anstatt den Fehler mit dem Zeitschritt zwischen den Abtastungen zu multiplizieren und dann zum nächsten Fehler multipliziert mit der Zeit zu addieren, können Sie einfach jede Fehlerabtastung mit einer Zeit von 1 multiplizieren. Das Ergebnis ist, dass Sie einfach eine laufende Summe von Fehlermessungen für Ihre Integralberechnung behalten können. Das folgende Beispiel zeigt, wie dies mit PBASIC zu bewerkstelligen ist:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
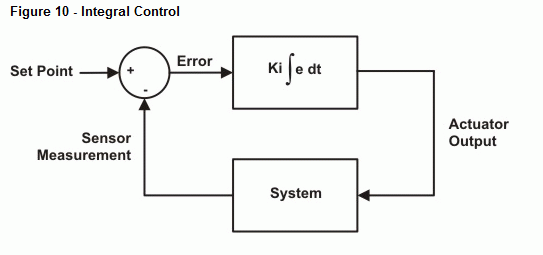
Das nächste Beispielprogramm führt eine numerische Integration des Fehlersignals durch und passt den Ausgang entsprechend an. Wie bei der Proportionalsteuerung gibt es eine Konstante, die den Integrationsausgang auf den gewünschten Wert skaliert. Der Einfachheit halber verwenden wir wieder 10 für Ki. Abbildung 10 zeigt ein Blockdiagramm des Regelkreises. Der Ausdruck Kp ∫ edt bezieht sich auf Kp multipliziert mit dem Integral des Fehlers über die Zeit. Mit anderen Worten: Kp multipliziert mit der akkumulierten Fläche zwischen der Fehlerkurve und der Zeitachse.
Beispielprogramm – IntegralAlgorithmus.bs2
- Eingeben, speichern und ausführen von IntegralAlgorithmus.bs2.
- Diese Folge von Werten in das Sendefenster des Debug-Terminals eingeben: 3 3 3 3 3 3 3 3 3. Beachten Sie, dass die Ausgabe des Integrals bei jeder Wiederholung der 3 größer wird. Das ist die Aufgabe des Integrals, Trends zu erkennen und den Antrieb zu erhöhen, um ihn bei Bedarf zu korrigieren.
- Nun versuchen Sie diese Sequenz: 1 2 3 4 5 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0. Die Fläche unter dieser Kurve ist 0, da die negative Fläche gleich der positiven Fläche ist. Das ist auch das Ergebnis der Integralberechnung, wenn Sie die Sequenz eingegeben haben.
' IntegralAlgorithm.bs2' Demonstrates how integral control influences error correction' in a feedback loop. ' {$STAMP BS2}' {$PBASIC 2.5} SetPoint CON 0 ' Set pointKi CON 10 ' Integral constant Current CON 0 ' Array index for current errorAccumulator CON 1 ' Array index for accumulated error sensorInput VAR Word ' Inputerror VAR Word(2) ' Two element error arrayi VAR Word ' Integral termdrive VAR Word ' Output DO DEBUG "Enter sensor input value: " DEBUGIN SDEC sensorInput ' Calculate error. error(Current) = SetPoint - sensorInput ' Calculate integral term. error(Accumulator) = error(Accumulator) + error(Current) i = Ki * error(Accumulator) ' Calculate output. drive = i ' Display values. DEBUG CR, CR, "ERROR", CR, SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR, "INTEGRAL", CR, SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR, "OUTPUT", CR, SDEC ? i, SDEC ? drive, CR, CR LOOP
Wie IntegralAlgorithm.bs2 funktioniert
Dieses Programm ist ein ProportionalAlgorithm.bs2, das modifiziert wurde, um stattdessen die Integralberechnung durchzuführen. Es gibt jetzt zwei verschiedene Arten von Fehlern, die verfolgt werden müssen, daher wurde das Array der Fehlervariablen auf zwei Elemente erweitert. Die Variable error(0) verfolgt den aktuellen Fehler, und error(1) verfolgt den kumulierten Fehler. Die Konstanten Current CON 0 und Accumulator CON 1 machen die Buchhaltung mit error(current) und error(accumulator) etwas sinnvoller.
Die andere Änderung, die vorgenommen wurde, ist, dass der Fehler akkumuliert wird und der Integralausgang mit diesen beiden Anweisungen berechnet wird:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
Your Turn – Clamping the Integral Output
Wie Sie vielleicht aus der wiederholten Eingabe von 3 in das Debug-Terminal erfahren haben, kann der Integralausgang des Antriebs wirklich anfangen zu laufen. Sie können die MIN- und MAX-Operatoren verwenden, um zu verhindern, dass die Integralsteuerung mit dem Ausgang über das Ziel hinausschießt. Wiederholen wir die Servo-Offset-Aktivität und begrenzen die Ausgabe von 650 bis 850.
- Ändern Sie die Anweisung drive = i in drive = i + Offset MIN 650 MAX 850.
- Starten Sie das Programm und überprüfen Sie, ob die Integralausgabe auf Werte zwischen 650 und 850 begrenzt ist. Versuchen Sie, wiederholt 2 und dann wiederholt -2 einzugeben.