Pi-Formeln

Posted on by admin
Zahlentheorie > Konstanten > Pi >
Kalkül und Analysis > Reihen > BBP-Formeln >
Kalkül und Analysis > Kalkül > Integrale > Definite Integrale >
MathWorld Mitwirkende > Cloitre >
MathWorld Mitwirkende > Plouffe >
MathWorld Mitwirkende > Sondow >

Less…

DOWNLOAD Mathematica Notebook

Es gibt viele Formeln von pi von vielen Typen. Dazu gehören unter anderem Reihen, Produkte, geometrische Konstruktionen, Grenzwerte, spezielle Werte und Pi-Wiederholungen.

pi steht in engem Zusammenhang mit den Eigenschaften von Kreisen und Kugeln. Für einen Kreis mit dem Radius r, sind Umfang und Fläche gegeben durch

C = 2pir
(1)
A = pir^2.
(2)

Also, für eine Kugel mit dem Radius r, sind die Oberfläche und das eingeschlossene Volumen

S = 4pir^2
(3)
V = 4/3pir^3.
(4)

Eine exakte Formel für pi in Form der inversen Tangens von Einheitsbrüchen ist die Machinsche Formel

1/4pi=4tan^(-1)(1/5)-tan^(-1)(1/(239)).
(5)

Es gibt drei weitere Machin-ähnliche Formeln, sowie Tausende von anderen ähnlichen Formeln mit mehr Termen.

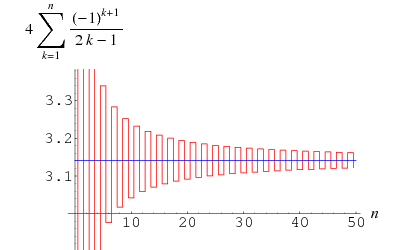
GregorySeries

Gregory und Leibniz fanden

pi/4 = Summe_(k=1)^(infty)((-1)^(k+1))/(2k-1)
(6)
= 1-1/3+1/5-...
(7)

(Wells 1986, S. 50), die als Gregory-Reihe bekannt ist und durch Einsetzen von x=1 in die Leibniz-Reihe für tan^(-1)x erhalten werden kann. Der Fehler nach dem n-ten Term dieser Reihe in der Gregory-Reihe ist größer als (2n)^(-1), so dass diese Summe so langsam konvergiert, dass 300 Terme nicht ausreichen, um pi korrekt auf zwei Dezimalstellen zu berechnen! Sie lässt sich aber umformen zu

pi=sum_(k=1)^infty(3^k-1)/(4^k)zeta(k+1),
(8)

wobei zeta(z) die Riemannsche Zeta-Funktion ist (Vardi 1991, pp. 157-158; Flajolet und Vardi 1996), so dass der Fehler nach k Termen ca. (3/4)^k ist.

Eine unendliche Summenreihe nach Abraham Sharp (ca. 1717) ist gegeben durch

pi=sum_(k=0)^infty(2(-1)^k3^(1/2-k))/(2k+1)
(9)

(Smith 1953, S. 311). Weitere einfache Reihen, in denen pi erscheint, sind

1/4pisqrt(2) = Summe_(k=1)^(infty)
(10)
= 1+1/3-1/5-1/7+1/9+1/(11)-...
(11)
1/4(pi-3) = Summe_(k=1)^(infty)((-1)^(k+1))/(2k(2k+1)(2k+2))
(12)
= 1/(2-3-4)-1/(4-5-6)+1/(6-7-8)-...
(13)
1/6pi^2 = Summe_(k=1)^(infty)1/(k^2)
(14)
= 1+1/4+1/9+1/(16)+1/(25)+...
(15)
1/8pi^2 = Summe_(k=1)^(infty)1/((2k-1)^2)
(16)
= 1+1/(3^2)+1/(5^2)+1/(7^2)+....
(17)

(Wells 1986, S. 53).

Im Jahre 1666, Newton benutzte eine geometrische Konstruktion zur Herleitung der Formel

pi = 3/4sqrt(3)+24int_0^(1/4)sqrt(x-x^2)dx
(18)
= (3sqrt(3))/4+24(1/(12)-1/(5-2^5)-1/(28-2^7)-1/(72-2^9)-...),
(19)

, die er zur Berechnung von pi verwendete (Wells 1986, S. 50; Borwein et al. 1989; Borwein und Bailey 2003, S. 105-106). Die Koeffizienten lassen sich aus dem Integral

I(x) = intsqrt(x-x^2)dx
(20)
= 1/4(2x-1)sqrt(x-x^2)-1/8sin^(-1)(1-2x)
(21)

durch die Reihenentwicklung von I(x)-I(0) um 0, obtaining

I(x)=2/3x^(3/2)-1/5x^(5/2)-1/(28)x^(7/2)-1/(72)x^(9/2)-5/(704)x^(11/2)+...
(22)

(OEIS A054387 und A054388). Die Anwendung der Eulerschen Konvergenzverbesserungstransformation ergibt

pi/2 = 1/2sum_(n=0)^(infty)((n!)^22^(n+1))/((2n+1)!)=sum_(n=0)^(infty)(n!)/((2n+1)!!)
(23)
= 1+1/3+(1-2)/(3-5)+(1-2-3)/(3-5-7)+...
(24)
= 1+1/3(1+2/5(1+3/7(1+4/9(1+...))))
(25)

(Beeler et al. 1972, Item 120).

Das entspricht dem Einsetzen von x=1/sqrt(2) in die Potenzreihe für die hypergeometrische Funktion _2F_1(a,b;c;x),

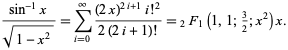(sin^(-1)x)/(sqrt(1-x^2))=sum_(i=0)^infty((2x)^(2i+1)i!^2)/(2(2i+1)!)=_2F_1(1,1;3/2;x^2)x.
(26)

Trotz der Konvergenzverbesserung konvergiert die Reihe (◇) nur mit einem Bit/Term. Auf Kosten einer Quadratwurzel hat Gosper festgestellt, dass x=1/2 2 Bit/Term ergibt,

1/9sqrt(3)pi=1/2sum_(i=0)^infty((i!)^2)/((2i+1)!),
(27)

und x=sin(pi/10) ergibt fast 3.39 Bit/Term,

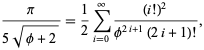pi/(5sqrt(phi+2))=1/2sum_(i=0)^infty((i!)^2)/(phi^(2i+1)(2i+1)!),
(28)

wobei phi der Goldene Schnitt ist. Gosper erhielt auch

pi=3+1/(60)(8+(2-3)/(7-8-3)(13+(3-5)/(10-11-3)(18+(4-7)/(13-14-3)(23+...)))).
(29)

Ein Zapfenalgorithmus für pi wird von Rabinowitz und Wagon (1995; Borwein und Bailey 2003, S. 141-142) angegeben.

Noch erstaunlicher ist, dass Bailey et al. eine geschlossene Formel für einen Algorithmus zur Extraktion von Ziffern zur Basis 16 gefunden haben, der Ziffern von pi (oder pi^2) erzeugt. (Bailey et al. 1997, Adamchik and Wagon 1997),

pi=sum_(n=0)^infty(4/(8n+1)-2/(8n+4)-1/(8n+5)-1/(8n+6))(1/(16))^n.
(30)

Diese Formel, bekannt als BBP-Formel, wurde mit Hilfe des PSLQ-Algorithmus (Ferguson et al. 1999) entdeckt und ist äquivalent zu

pi=int_0^1(16y-16)/(y^4-2y^3+4y-4)dy.
(31)

Es gibt eine Reihe von BBP-artigen Formeln für pi in Potenzen von (-1)^k, die ersten paar unabhängigen Formeln davon sind

pi = 4sum_(k=0)^(infty)((-1)^k)/(2k+1)
(32)
= 3Summe_(k=0)^(infty)(-1)^k
(33)
= 4Summe_(k=0)^(infty)(-1)^k
(34)
= Summe_(k=0)^(infty)(-1)^k
(35)
= Summe_(k=0)^(infty)(-1)^k
(36)
= Summe_(k=0)^(infty)(-1)^k.
(37)

Auch für pi gibt es eine Reihe von BBP-artigen Formeln in Potenzen von 2^k, die ersten paar unabhängigen Formeln davon sind

pi = sum_(k=0)^(infty)1/(16^k)
(38)
= 1/2Summe_(k=0)^(infty)1/(16^k)
(39)
= 1/(16)sum_(k=0)^(infty)1/(256^k)
(40)
= 1/(32)sum_(k=0)^(infty)1/(256^k)
(41)
= 1/(32)Summe_(k=0)^(infty)1/(4096^k)
(42)
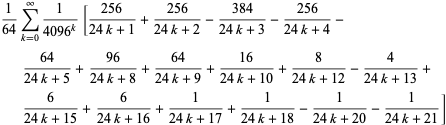= 1/(64)sum_(k=0)^(infty)1/(4096^k)
(43)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(44)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(45)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(46)
= 1/(4096)sum_(k=0)^(infty)1/(65536^k)
(47)
= 1/(4096)sum_(k=0)^(infty)1/(65536^k).
(48)

F. Bellard fand die schnell konvergierende BBP-Typenformel

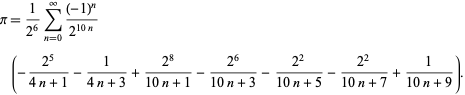pi=1/(2^6)sum_(n=0)^infty((-1)^n)/(2^(10n))(-(2^5)/(4n+1)-1/(4n+3)+(2^8)/(10n+1)-(2^6)/(10n+3)-(2^2)/(10n+5)-(2^2)/(10n+7)+1/(10n+9)).
(49)

Ein verwandtes Integral ist

pi=(22)/7-int_0^1(x^4(1-x)^4)/(1+x^2)dx
(50)

(Dalzell 1944, 1971; Le Lionnais 1983, p. 22; Borwein, Bailey, und Girgensohn 2004, S. 3; Boros und Moll 2004, S. 125; Lucas 2005; Borwein et al. 2007, S. 14). Dieses Integral war K. Mahler Mitte der 1960er Jahre bekannt und taucht in einer Prüfung an der Universität von Sydney im November 1960 auf (Borwein, Bailey, und Girgensohn, S. 3). Beukers (2000) und Boros und Moll (2004, S. 126) stellen fest, dass es nicht klar ist, ob es eine natürliche Wahl eines rationalen Polynoms gibt, dessen Integral zwischen 0 und 1 pi-333/106 ergibt, wobei 333/106 das nächste konvergente Integral ist. Es gibt jedoch ein Integral für den vierten Konvergenten, nämlich

pi=(355)/(113)-1/(3164)int_0^1(x^8(1-x)^8(25+816x^2))/(1+x^2)dx.
(51)

(Lucas 2005; Bailey et al. 2007, S. 219). In der Tat gibt Lucas (2005) einige weitere solche Integrale an.

Backhouse (1995) verwendet die Identität

I_(m,n) = int_0^1(x^m(1-x)^n)/(1+x^2)dx
(52)
= 2^(-(m+n+1))sqrt(pi)Gamma(m+1)Gamma(n+1)×_3F_2(1,(m+1)/2,(m+2)/2;(m+n+2)/2,(m+n+3)/2;-1)
(53)
= a+bpi+cln2
(54)

für positive ganze Zahlen m und n und wobei a, b und c rationale Konstanten sind, um eine Reihe von Formeln für pi zu erzeugen. Insbesondere, wenn 2m-n=0 (mod 4), dann c=0 (Lucas 2005).

Eine ähnliche Formel wurde später von Ferguson entdeckt, was zu einem zweidimensionalen Gitter solcher Formeln führt, das durch diese beiden Formeln erzeugt werden kann, gegeben durch

pi=sum_(k=0)^infty((4+8r)/(8k+1)-(8r)/(8k+2)-(4r)/(8k+3)-(2+8r)/(8k+4)-(1+2r)/(8k+5)-(1+2r)/(8k+6)+r/(8k+7))(1/(16))^k
(55)

für jeden komplexen Wert von r (Adamchik und Wagon), was die BBP-Formel für den Spezialfall r=0 ergibt.

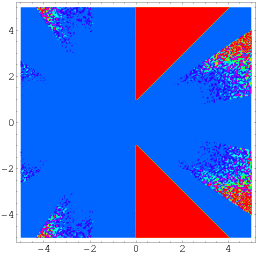
PiFormulasWagonIdentity

Eine noch allgemeinere Identität nach Wagon ist gegeben durch

pi+4tan^(-1)z+2ln((1-2z-z^2)/(z^2+1))=sum_(k=0)^infty1/(16^k)
(56)

(Borwein und Bailey 2003, p. 141), die für einen Bereich der komplexen Ebene gilt, der zwei dreieckige Teile ausschließt, die symmetrisch um die reelle Achse angeordnet sind, wie oben dargestellt.

Eine vielleicht noch allgemeinere Klasse von Identitäten ist gegeben durch

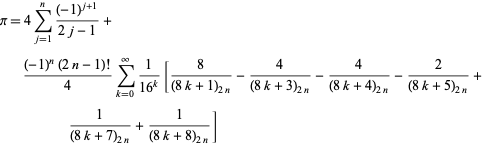pi=4sum_(j=1)^n((-1)^(j+1))/(2j-1)+((-1)^n(2n-1)!)/4sum_(k=0)^infty1/(16^k)
(57)

was für jede positive ganze Zahl n gilt, wobei (x)_n ein Pochhammer-Symbol ist (B. Cloitre, pers. Mitt, Jan. 23, 2005). Noch erstaunlicher ist, dass es eine sehr analoge Formel für den natürlichen Logarithmus von 2 gibt.

Nach der Entdeckung der BBP-Formel zur Basis 16 und verwandter Formeln wurden ähnliche Formeln in anderen Basen untersucht. Borwein, Bailey und Girgensohn (2004) haben kürzlich gezeigt, dass pi keine BBP-Arkustangens-Formel vom Machin-Typ hat, die nicht binär ist, obwohl dies ein völlig anderes Schema für Ziffern-Extraktionsalgorithmen in anderen Basen nicht ausschließt.

S. Plouffe hat einen Algorithmus entwickelt, um die n-te Stelle von pi in jeder Basis in O(n^3(logn)^3) Schritten zu berechnen.

Eine Reihe weiterer Identitäten, die auf Ramanujan, Catalan und Newton zurückgehen, werden von Castellanos (1988ab, S. 86-88) angegeben, darunter mehrere, die Summen von Fibonacci-Zahlen betreffen. Ramanujan fand

sum_(k=0)^infty((-1)^k(4k+1)^3)/(^3)=sum_(k=0)^infty((-1)^k(4k+1)^3)/(pi^(3/2)^3)=2/pi
(58)

(Hardy 1923, 1924, 1999, p. 7).

Plouffe (2006) fand die schöne Formel

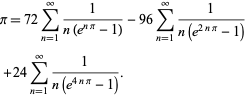pi=72sum_(n=1)^infty1/(n(e^(npi)-1))-96sum_(n=1)^infty1/(n(e^(2npi)-1)) +24sum_(n=1)^infty1/(n(e^(4npi)-1)).
(59)

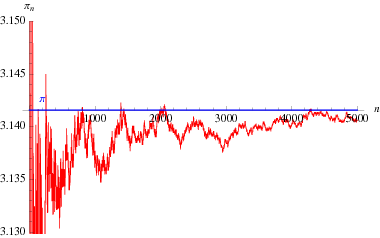
PiBlatnerProduct

Eine interessante, auf Euler zurückgehende unendliche Produktformel, die pi und die nte Primzahl p_n in Beziehung setzt, lautet

pi = 2/(Produkt_(n=1)^(infty))
(60)
= 2/(Produkt_(n=2)^(infty))
(61)

(Blatner 1997, p. 119), die oben als Funktion der Anzahl der Terme im Produkt aufgetragen ist.

Eine Methode, die der von Archimedes ähnelt, kann verwendet werden, um pi abzuschätzen, indem man mit einem n-Gon beginnt und dann die Fläche der nachfolgenden 2n-Gons in Beziehung setzt. Sei beta der Winkel von der Mitte eines der Segmente des Polygons,

beta=1/4(n-3)pi,
(62)

dann

pi=(2sin(2beta))/((n-3)Produkt_(k=0)^(infty)cos(2^(-k)beta))
(63)

(Beckmann 1989, pp. 92-94).

Vieta (1593) war der erste, der einen exakten Ausdruck für pi lieferte, indem er n=4 in den obigen Ausdruck einsetzte, was

cosbeta=sinbeta=1/(sqrt(2))=1/2sqrt(2) ergab,
(64)

was zu einem unendlichen Produkt von verschachtelten Radikalen führt,

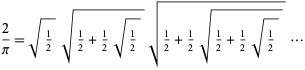2/pi=sqrt(1/2)sqrt(1/2+1/2sqrt(1/2))sqrt(1/2+1/2sqrt(1/2+1/2sqrt(1/2)))...
(65)

(Wells 1986, S. 50; Beckmann 1989, S. 95). Allerdings wurde die Konvergenz dieses Ausdrucks erst von Rudio 1892 rigoros bewiesen.

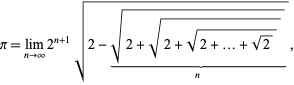
Eine verwandte Formel ist gegeben durch

pi=lim_(n-infty)2^(n+1)sqrt(2-sqrt(2+sqrt(2+sqrt(2+...+sqrt(2))))_()_(n)),
(66)

was geschrieben werden kann

pi=lim_(n-infty)2^(n+1)pi_n,
(67)

wobei pi_n mit Hilfe der Iteration definiert wird

pi_n=sqrt((1/2pi_(n-1))^2+^2)
(68)

mit pi_0=sqrt(2) (J. Munkhammar, pers. Mitt, April 27, 2000). Die Formel

pi=2lim_(m-infty)sum_(n=1)^msqrt(^2+1/(m^2))
(69)

ist ebenfalls eng verwandt.

Eine schöne Formel für pi ist gegeben durch

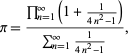pi=(Produkt_(n=1)^(infty)(1+1/(4n^2-1)))/(Summe_(n=1)^(infty)1/(4n^2-1)),
(70)

wobei der Zähler eine Form der Wallis-Formel für pi/2 ist und der Nenner eine Teleskopsumme mit Summe 1/2 ist, da

1/(4n^2-1)=1/2(1/(2n-1)-1/(2n+1))
(71)

(Sondow 1997).

Ein Sonderfall der Wallis-Formel ergibt

pi/2=Produkt_(n=1)^infty=(2-2)/(1-3)(4-4)/(3-5)(6-6)/(5-7)...
(72)

(Wells 1986, S. 50). Diese Formel kann auch geschrieben werden

lim_(n-infty)(2^(4n))/(n(2n; n)^2)=pilim_(n-infty)(n^2)/(^2)=pi,
(73)

wobei (n; k) einen Binomialkoeffizienten bezeichnet und Gamma(x) die Gammafunktion ist (Knopp 1990). Euler erhielt

pi=sqrt(6(1+1/(2^2)+1/(3^2)+1/(4^2)+...)),
(74)

was aus dem speziellen Wert der Riemannschen Zeta-Funktion zeta(2)=pi^2/6 folgt. Ähnliche Formeln folgen aus zeta(2n) für alle positiven ganzen Zahlen n.

Eine unendliche Summe nach Ramanujan ist

1/pi=sum_(n=0)^infty(2n; n)^3(42n+5)/(2^(12n+4))
(75)

(Borwein et al. 1989; Borwein und Bailey 2003, S. 109; Bailey et al.2007, S. 44). Weitere Summen sind in Ramanujan (1913-14) angegeben,

4/pi=sum_(n=0)^infty((-1)^n(1123+21460n)(2n-1)!!(4n-1)!!)/(882^(2n+1)32^n(n!)^3)
(76)

und

1/pi = sqrt(8)sum_(n=0)^(infty)((1103+26390n)(2n-1)!!(4n-1)!!)/(99^(4n+2)32^n(n!)^3)
(77)
= (sqrt(8))/(9801)sum_(n=0)^(infty)((4n)!(1103+26390n))/((n!)^4396^(4n))
(78)

(Beeler et al. 1972, Punkt 139; Borwein et al. 1989; Borwein und Bailey 2003, S. 108; Bailey et al. 2007, S. 44). Gleichung (78) wird von einer modularen Identität der Ordnung 58 abgeleitet, obwohl eine erste Ableitung erst von Borwein und Borwein (1987) vorgelegt wurde. Die obigen Reihen ergeben beide

pi approx (9801)/(2206sqrt(2))=3.14159273001...
(79)

(Wells 1986, S. 54) als erste Näherung und liefern etwa 6 bzw. 8 Dezimalstellen pro Term. Solche Reihen existieren aufgrund der Rationalität verschiedener modularer Invarianten.

Die allgemeine Form der Reihe ist

sum_(n=0)^infty((6n)!)/((3n)!(n!)^3)1/(^n)=(sqrt(-j(t)))/pi,
(80)

wobei t eine binäre quadratische Formdiskriminante ist, j(t) ist die j-Funktion,

b(t) = sqrt(t)
(81)
a(t) = (b(t))/6{1-(E_4(t))/(E_6(t))},
(82)

und die E_i sind Eisensteinreihen. Ein Feld der Klassenzahl p besteht aus algebraischen ganzen Zahlen p dritten Grades mit den Konstanten A=a(t), B=b(t) und C=c(t). Von allen Reihen, die nur aus ganzzahligen Termen bestehen, entspricht diejenige, die die meisten numerischen Ziffern in der kürzesten Zeit liefert, der größten Diskriminante der Klasse 1 von d=-163 und wurde von den Brüdern Chudnovsky (1987) formuliert. Die 163, die hier auftaucht, ist dieselbe, die in der Tatsache auftaucht, dass e^(pisqrt(163)) (die Ramanujan-Konstante) fast eine ganze Zahl ist. In ähnlicher Weise stammt der Faktor 640320^3 aus der j-Funktionsidentität für j(1/2(1+isqrt(163))). Die Reihe ist gegeben durch

1/pi = 12sum_(n=0)^(infty)((-1)^n(6n)!(13591409+545140134n))/((n!)^3(3n)!(640320^3)^(n+1/2))
(83)
= (163·8·27·7·11·19·127)/(640320^(3/2))sum_(n=0)^(infty)((13591409)/(163·2·9·7·11·19·127)+n)((6n)!)/((3n)!(n!)^3)((-1)^n)/(640320^(3n))
(84)

(Borwein und Borwein 1993; Beck und Trott; Bailey et al. 2007, S. 44). Diese Reihe ergibt genau 14 Ziffern pro Term. Die gleiche Gleichung in anderer Form wurde von den Gebrüdern Chudnovsky (1987) aufgestellt und wird von der Wolfram Language zur Berechnung von pi verwendet (Vardi 1991; Wolfram Research),

pi=(426880sqrt(10005))/(A),
(85)

wobei

A = 13591409
(86)
B = -1/(151931373056000)
(87)
C = (30285563)/(1651969144908540723200).
(88)

Die beste Formel für die Klasse Nummer 2 (größte Diskriminante -427) ist

1/pi=12sum_(n=0)^infty((-1)^n(6n)!(A+Bn))/((n!)^3(3n)!C^(n+1/2)),
(89)

wobei

A = 212175710912sqrt(61)+1657145277365
(90)
B = 13773980892672sqrt(61)+107578229802750
(91)
C = ^3
(92)

(Borwein und Borwein 1993). Diese Reihe fügt etwa 25 Stellen für jeden zusätzlichen Term hinzu. Die am schnellsten konvergierende Reihe für Klasse 3 entspricht d=-907 und ergibt 37-38 Ziffern pro Term. Die am schnellsten konvergierende Reihe der Klasse 4 entspricht d=-1555 und ist

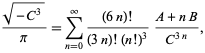(sqrt(-C^3))/pi=sum_(n=0)^infty((6n)!)/((3n)!(n!)^3)(A+nB)/(C^(3n)),
(93)

wobei

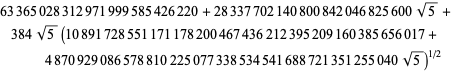A = 63365028312971999585426220+28337702140800842046825600sqrt(5)+384sqrt(5)(10891728551171178200467436212395209160385656017+4870929086578810225077338534541688721351255040sqrt(5))^(1/2)
(94)
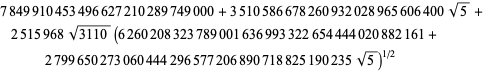B = 7849910453496627210289749000+3510586678260932028965606400sqrt(5)+2515968sqrt(3110)(6260208323789001636993322654444020882161+2799650273060444296577206890718825190235sqrt(5))^(1/2)
(95)
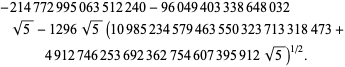C = -214772995063512240-96049403338648032sqrt(5)-1296sqrt(5)(10985234579463550323713318473+4912746253692362754607395912sqrt(5))^(1/2).
(96)

Das ergibt 50 Ziffern pro Term. Borwein und Borwein (1993) haben einen allgemeinen Algorithmus zur Erzeugung solcher Reihen für beliebige Klassenzahlen entwickelt.

Eine vollständige Auflistung von Ramanujans Reihen für 1/pi, die in seinem zweiten und dritten Notizbuch gefunden wurden, findet sich bei Berndt (1994, pp. 352-354),

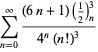4/pi = sum_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!)^3)
(97)
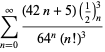(16)/pi = Summe_(n=0)^(infty)((42n+5)(1/2)_n^3)/(64^n(n!)^3)
(98)
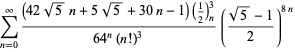(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(99)
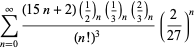(27)/(4pi) = sum_(n=0)^(infty)((15n+2)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(2/(27))^n
(100)
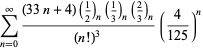(15sqrt(3))/(2pi) = sum_(n=0)^(infty)((33n+4)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(4/(125))^n
(101)
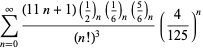(5sqrt(5))/(2pisqrt(3)) = sum_(n=0)^(infty)((11n+1)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(125))^n
(102)
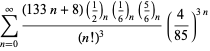(85sqrt(85))/(18pisqrt(3)) = sum_(n=0)^(infty)((133n+8)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(85))^(3n)
(103)
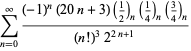4/pi = sum_(n=0)^(infty)((-1)^n(20n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^32^(2n+1))
(104)
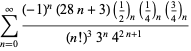4/(pisqrt(3)) = sum_(n=0)^(infty)((-1)^n(28n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^33^n4^(2n+1))
(105)
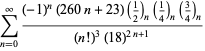4/pi = sum_(n=0)^(infty)((-1)^n(260n+23)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(18)^(2n+1))
(106)
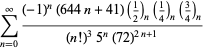4/(pisqrt(5)) = sum_(n=0)^(infty)((-1)^n(644n+41)(1/2)_n(1/4)_n(3/4)_n)/((n!)^35^n(72)^(2n+1))
(107)
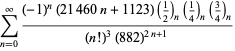4/pi = sum_(n=0)^(infty)((-1)^n(21460n+1123)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(882)^(2n+1))
(108)
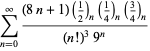(2sqrt(3))/pi = sum_(n=0)^(infty)((8n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^n)
(109)
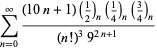1/(2pisqrt(2)) = sum_(n=0)^(infty)((10n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^(2n+1))
(110)
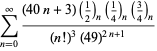1/(3pisqrt(3)) = sum_(n=0)^(infty)((40n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(49)^(2n+1))
(111)
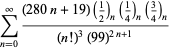2/(pisqrt(11)) = sum_(n=0)^(infty)((280n+19)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(2n+1))
(112)
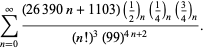1/(2pisqrt(2)) = sum_(n=0)^(infty)((26390n+1103)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(4n+2)).
(113)

Diese Gleichungen wurden erstmals von Borwein und Borwein (1987a, S. 177-187) nachgewiesen. Borwein und Borwein (1987b, 1988, 1993) bewiesen weitere Gleichungen dieser Art, und Chudnovsky und Chudnovsky (1987) fanden ähnliche Gleichungen für andere transzendente Konstanten (Bailey et al. 2007, S. 44-45).

Eine vollständige Liste von unabhängigen bekannten Gleichungen dieses Typs ist gegeben durch

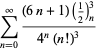4/pi = sum_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!)^3)
(114)
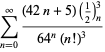(16)/pi = Summe_(n=0)^(infty)((42n+5)(1/2)_n^3)/(64^n(n!)^3)
(115)
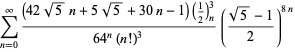(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(116)
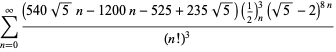(5^(1/4))/pi = sum_(n=0)^(infty)((540sqrt(5)n-1200n-525+235sqrt(5))(1/2)_n^3(sqrt(5)-2)^(8n))/((n!)^3)
(117)
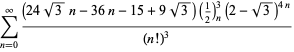(12^(1/4))/pi = Summe_(n=0)^(infty)((24sqrt(3)n-36n-15+9sqrt(3))(1/2)_n^3(2-sqrt(3))^(4n))/((n!)^3)
(118)

für m=1 mit nicht-wechselnden Vorzeichen,

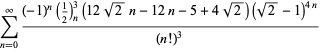2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(12sqrt(2)n-12n-5+4sqrt(2))(sqrt(2)-1)^(4n))/((n!)^3)
(119)
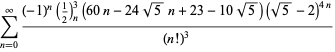2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(60n-24sqrt(5)n+23-10sqrt(5))(sqrt(5)-2)^(4n))/((n!)^3)
(120)
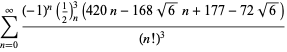2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(420n-168sqrt(6)n+177-72sqrt(6)))/((n!)^3)
(121)
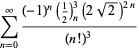(2sqrt(2))/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(2sqrt(2))^(2n))/((n!)^3)
(122)

für m=1 mit wechselnden Vorzeichen,

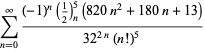(128)/(pi^2) = Summe_(n=0)^(infty)((-1)^n(1/2)_n^5(820n^2+180n+13))/(32^(2n)(n!)^5)
(123)
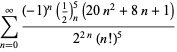(32)/(pi^2) = sum_(n=0)^(infty)((-1)^n(1/2)_n^5(20n^2+8n+1))/(2^(2n)(n!)^5)
(124)

für m=2 (Guillera 2002, 2003, 2006),

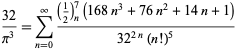(32)/(pi^3)=sum_(n=0)^infty((1/2)_n^7(168n^3+76n^2+14n+1))/(32^(2n)(n!)^5)
(125)

für m=3 (Guillera 2002, 2003, 2006), und keine weiteren für m3 sind bekannt (Bailey et al. 2007, S. 45-48).

Bellard gibt die exotische Formel

pi=1/(740025),
(126)

where

P(n)=-885673181n^5+3125347237n^4-2942969225n^3+1031962795n^2-196882274n+10996648.
(127)

Gasper zitiert das Ergebnis

pi=(16)/3^(-1),
(128)

wobei _1F_2 eine verallgemeinerte hypergeometrische Funktion ist, und transformiert es zu

pi=lim_(x-infty)4x_1F_2(1/2;3/2,3/2;-x^2).
(129)

Ein faszinierendes Ergebnis nach Gosper ist gegeben durch

lim_(n-infty)product_(i=n)^(2n)pi/(2tan^(-1)i)=4^(1/pi)=1.554682275....
(130)

pi erfüllt die Ungleichung

(1+1/pi)^(pi+1) approx 3.14097pi.
(131)

D. Terr (pers. Mitt.) bemerkte die merkwürdige Identität

(3,1,4)=(1,5,9)+(2,6,5) (mod 10)
(132)

mit den ersten 9 Ziffern von pi.

Schreibe einen Kommentar

Deine E-Mail-Adresse wird nicht veröffentlicht.