Rotationskinematik - Physik 298

„Die Menschen reden davon, die Zeit zu töten, während die Zeit sie leise tötet“
Dion Boucicault – London Assurance (1841)

Bislang haben wir die Kinematik und Dynamik von Teilchen, einschließlich der Translations- und Kreisbewegung, sowie die Translationsbewegung von Systemen von Teilchen (insbesondere von starren Körpern) in Bezug auf die Bewegung des Massenschwerpunkts des Systems (Körpers) betrachtet. Im letzteren Fall können wir uns vorstellen, dass sich die gesamte Masse des Objekts im Massenschwerpunkt befindet, soweit es sich um äußere Translationskräfte handelt.

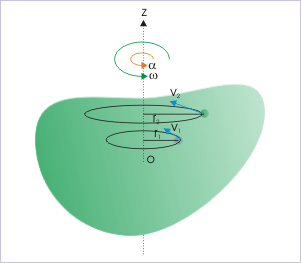Der nächste Schritt ist die Betrachtung der Rotation eines starren Körpers um eine feste Drehachse. Da wir einen starren Körper betrachten, bleibt jedes Teilchen in diesem Körper relativ zu den anderen fest. Das bedeutet, dass sich bei einer solchen Rotationsbewegung jedes Teilchen auf einem Kreis bewegt, dessen Mittelpunkt auf der Rotationsachse liegt. Im Diagramm rechts rotiert das Objekt um die z-Achse; die beiden Beispielteilchen bewegen sich auf Kreisen mit den Radien r1 und r2. Wenn wir die Kreisbewegung eines Teilchens beschreiben können, ohne direkt auf seinen Radius Bezug zu nehmen, dann werden alle Teilchen im System durch denselben Satz von Gleichungen beschrieben. Obwohl die Radien der Teilchen unterschiedlich sind, sind ihre Winkeldrehungen identisch. Daher ist es notwendig, Winkelvariablen einzuführen.

Winkelmaße

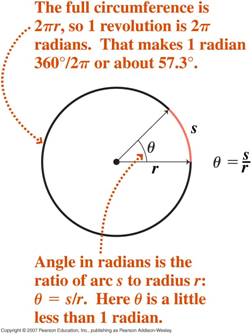
Winkelgeschwindigkeit (Geschwindigkeit) und Winkelbeschleunigung

Winkelgeschwindigkeit und Winkelbeschleunigung sind ähnlich definiert wie Geschwindigkeit und Beschleunigung. Es gibt Durchschnitts- und Momentanwerte.

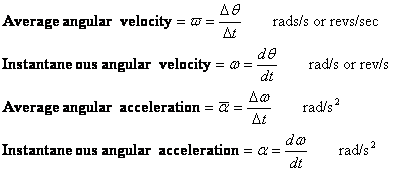
Die Winkelbeschleunigung ist nicht dasselbe wie die Zentripetalbeschleunigung. Die Zentripetalbeschleunigung ist auf eine Änderung der Richtung der Geschwindigkeit zurückzuführen, die Winkelbeschleunigung auf eine Änderung des Betrags der Geschwindigkeit (durch den Drehwinkel).

Genau wie im Fall der Translation ist der Unterschied zwischen Winkelgeschwindigkeit und Winkelgeschwindigkeit die Richtung. Die Winkelgeschwindigkeit muss eine Drehrichtung um die betreffende Achse beinhalten. Zum Beispiel ist 10 rad/s im Uhrzeigersinn um die x-Achse eine Winkelgeschwindigkeit, 10 rad/s um die x-Achse eine Winkelgeschwindigkeit.

Rotationskinematische Gleichungen

In direkter Analogie zu den Gleichungen der Translationskinematik kann die Kreisbewegung um eine einzelne Achse bei konstanter Winkelbeschleunigung durch die folgenden vier Gleichungen beschrieben werden,

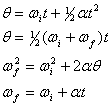
wobei wir die Substitutionen vorgenommen haben,

Beachten Sie, dass ebenso wie +x beliebig nach rechts definiert werden kann, der positive Wert von theta als im oder gegen den Uhrzeigersinn definiert werden kann.

Beziehung zwischen Winkel- und Translationsvariablen

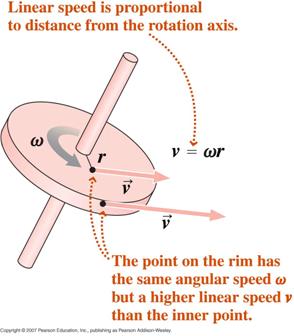Ausgehend von der Definition des Bogenmaßes können wir durch Differenzieren nach der Zeit zeigen,

wobei v die Tangentialgeschwindigkeit und a die Tangentialbeschleunigung ist.

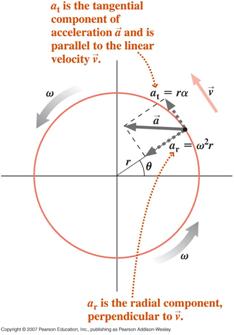
Ein Teilchen, das eine Kreisbewegung mit variierender Winkelgeschwindigkeit ausführt (nicht gleichförmige Kreisbewegung), erfährt zwei Komponenten der Beschleunigung, eine tangentiale Komponente aufgrund des sich ändernden Betrags seiner Geschwindigkeit und eine radiale (zentripetale) Komponente aufgrund der sich ändernden Richtung seiner Geschwindigkeit

Die Nettobeschleunigung des Teilchens ist die Vektorsumme dieser beiden Komponenten, wie unten angegeben.

Zu Ihrer Information…

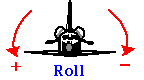
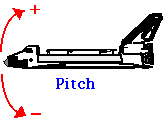
Die gleichzeitige Drehung um mehr als eine Achse kann auf ähnliche Weise wie die Projektilbewegung betrachtet werden, bei der wir unsere 1D-Translationsdiskussion auf die 2D-Bewegung ausgedehnt haben. In der Luftfahrt werden Rotationen um die drei Achsen als Roll, Pitch und Yaw bezeichnet.