Wie man sich auf die Geometrie-Fragen in einem Mathe-Test vorbereitet
Allgemeine Informationen
Geometrie ist nur ein schicker Name für das Studium von Linien und Formen. Es gibt sicherlich noch weitere schwierige Prinzipien und Themen, aber wir haben hier die Grundlagen. Sie müssen diese beherrschen, bevor Sie sich mit fortgeschritteneren Konzepten befassen können.
(Bitte beachten Sie, dass eine Abbildung, die in diesem Leitfaden als „Beispiel“ bezeichnet wird, nicht unbedingt die einzige Darstellung dieser Abbildung ist, aber eine von ihnen.)
Punkte und Linien
Ein Punkt in der Geometrie ist ein Ort. Er hat keine Länge, Breite oder Tiefe. Wir verwenden einen Punkt und einen Großbuchstaben, um einen Punkt darzustellen.
Ein Linienabschnitt wird durch zwei Punkte und alle Punkte zwischen ihnen definiert. Die beiden Punkte werden Endpunkte des Abschnitts genannt. Ein Segment hat eine Dimension: die Länge. Um ein Segment zu schreiben, setzt man einen Balken über die beiden Endpunkte. \(\overline{AB}\) oder \(\overline{BA}\) ist dieses Segment:

Eine Linie erstreckt sich in beide Richtungen ohne Ende. Um eine Linie zu schreiben, setzt man einen Balken mit zwei Pfeilen über zwei beliebige Punkte der Linie. \(\overleftrightarrow{AB}\) oder \(\overleftrightarrow{BA}\) ist die Linie:

Ein Strahl beginnt an einem Endpunkt und erstreckt sich ohne Ende in nur eine Richtung. Um einen Strahl zu schreiben, setzt man einen Balken mit einem Pfeil, der nach rechts zeigt, über zwei Punkte: den Endpunkt und einen beliebigen anderen Punkt (in dieser Richtung). \(\overrightarrow{AB}\) ist der Strahl:

Anmerkung: Sie können keinen Strahl schreiben, bei dem der Pfeil nach links zeigt, wie \(\overleftarrow{BA}\). Außerdem ist die Reihenfolge wichtig. \(\overrightarrow{BA}\) ist nicht dasselbe wie \(\overrightarrow{AB}\). Der erste Buchstabe ist immer der Anfangspunkt eines Strahls.
Zwei Linien, Segmente oder Strahlen sind senkrecht, wenn sie einen rechten Winkel bilden (siehe unten). Verwenden Sie das Symbol \(\perp\), um die Rechtwinkligkeit zu bezeichnen. Wenn zum Beispiel \(\overline{AB}\) senkrecht auf \(\overline{CD}\) steht, kann man \(\overline{AB} \perp \overline{CD}\) schreiben.
Beispiele: 
Zwei Linien sind parallel, wenn sie sich nie schneiden. Wenn \(\overleftrightarrow{AB}\) parallel zu \(\overleftrightarrow{CD}\) ist, kann man \(\overleftrightarrow{AB} \parallel \overleftrightarrow{CD}\) schreiben.
Beispiele: 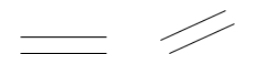
Ebene Formen
In der Geometrie ist eine Ebene eine ebene zweidimensionale Fläche, die sich unendlich weit erstreckt. Die beiden Dimensionen sind Länge und Breite. Daher sind ebene Formen „flache“ Formen, wie Quadrate, Kreise und Dreiecke.
Gebräuchliche Formen
Ein Polygon ist eine geschlossene Fläche in einer Ebene, die durch Liniensegmente, die Seiten genannt werden, begrenzt wird.
Beispiele: 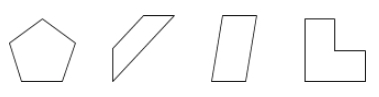
Ein regelmäßiges Vieleck ist ein Vieleck, bei dem alle Segmente und Innenwinkel kongruent sind.
Beispiele:
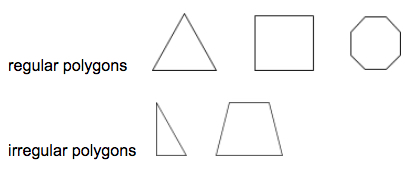
Ein Dreieck ist ein dreiseitiges Vieleck.
Beispiele:
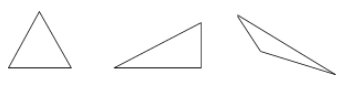
Vierecke – vierseitige Polygone
Ein Parallelogramm ist eine Art Viereck, bei dem die gegenüberliegenden Seiten parallel und kongruent sind. Die gegenüberliegenden Winkel eines Parallelogramms sind ebenfalls kongruent.
Beispiele: 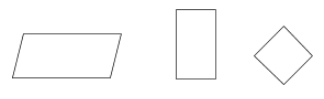
Ein Rechteck ist ein Parallelogramm mit vier rechten Winkeln.
Beispiele: 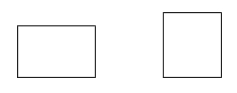
Ein Rhombus ist ein Parallelogramm, bei dem alle vier Seiten kongruent sind.
Beispiele: 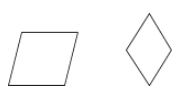
Ein Quadrat ist ein Parallelogramm, das sowohl ein Rhombus als auch ein Rechteck ist (alle Seiten sind kongruent und alle Winkel sind rechtwinklig).
Beispiele: 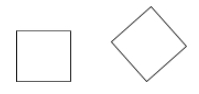
Ein Trapez ist ein Viereck mit nur einem Paar paralleler Seiten.
Beispiele: 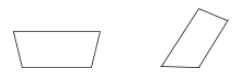
Polygone mit mehr als vier Seiten
\
\(^1\) Ein Polygon mit 11 Seiten kann auch als Endeck oder Undeck bezeichnet werden.
Messen von Formen
Der Umfang ist die Gesamtstrecke um ein Polygon. Um den Umfang zu ermitteln, addiert man einfach die Längen aller Seiten. Wenn das Polygon regelmäßig ist (alle Seiten sind kongruent) und die Länge einer Seite \(s\) ist, dann multipliziert man die Anzahl der Seiten mit \(s\), um den Umfang zu ermitteln. Zum Beispiel ist der Umfang eines regelmäßigen Fünfecks \(P_\text{reg pentagon}=5s\)