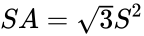Für die wissenschaftliche Zeitschrift, siehe Tetrahedron (Zeitschrift).
| Reguläres Tetraeder | |
|---|---|
 (Hier klicken für das rotierende Modell) |
|
| Typ | Platonischer Festkörper |
| Elemente | F = 4, E = 6 V = 4 (χ = 2) |
| Seitenflächen | 4{3} |
| Schläfli Symbol | {3,3} und s{2,2} |
| Wythoff-Symbol | 3 | 2 3 | 2 2 2 |
| Coxeter-Dynkin | |
| Symmetrie | Td oder (*332) |
| U01, C15, W1 | |
| Eigenschaften | Regelmäßiges konvexes Deltaeder |
| Dihedralwinkel | 70.528779° = arccos(1/3) |
 3.3.3 (Scheitelfigur) |
 Selbstdual (duales Polyeder) |
 Netz |
|
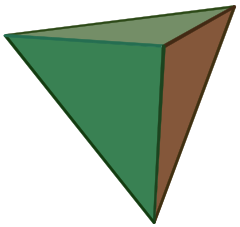
Ein Tetraeder (Plural: Tetraeder) ist ein Polyeder, das aus vier dreieckigen Flächen besteht, von denen sich drei an jedem Scheitelpunkt treffen. Ein regelmäßiges Tetraeder ist ein Polyeder, bei dem die vier Dreiecke regelmäßig oder „gleichseitig“ sind, und gehört zu den platonischen Körpern.
Das Tetraeder ist eine Art Pyramide, d. h. ein Polyeder mit einer flachen Polygonbasis und dreieckigen Flächen, die die Basis mit einem gemeinsamen Punkt verbinden. Im Falle eines Tetraeders ist die Basis ein Dreieck (jede der vier Flächen kann als Basis betrachtet werden), daher ist ein Tetraeder auch als Dreieckspyramide oder Digonaldeltaeder bekannt.
Formeln für reguläre Tetraeder
Das Volumen ist
Die Oberfläche ist
Vorlage:Commonscat
- F. M. Jackson und Weisstein, Eric W., „Tetrahedron“ aus MathWorld.
- Weisstein, Eric W., „Tetrahedron“ aus MathWorld.
- Weisstein, Eric W., „Tetrahedron“ aus MathWorld.
- The Uniform Polyhedra
- Tetrahedron: Interactive Polyhedron Model
- K. J. M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- Piero della Francesca’s formula for tetrahedron volume at MathPages
- Free paper models of a tetrahedron and many other polyhedra
- An Amazing, Raum füllendes, nicht-reguläres Tetraeder, das auch eine Beschreibung eines „rotierenden Rings von Tetraedern“, auch bekannt als Kaleidozyklus, enthält.
- Tetraeder-Kernnetz Anwendung einer tetraedrischen Struktur zur Schaffung eines belastbaren partiellen Maschendatennetzes
- Explizite exakte Formeln für den Trägheitstensor eines beliebigen Tetraeders in Form seiner Eckenkoordinaten
- Der Trägheitstensor eines Tetraeders