
Die Mathematik beschäftigt sich mit einer Vielzahl von Konzepten, die sehr wichtig, aber gleichzeitig auch komplex und zeitaufwendig sind. Python bietet jedoch die vollwertige Bibliothek SciPy, die dieses Problem für uns löst. In diesem SciPy-Tutorial lernen Sie, wie Sie diese Bibliothek zusammen mit einigen Funktionen und ihren Beispielen nutzen können.
Bevor Sie weitermachen, werfen Sie einen Blick auf alle in diesem Artikel behandelten Themen:
- Was ist SciPy?
- NumPy vs SciPy
- Unterpakete in SciPy
- Grundfunktionen
- Spezialfunktionen
- Integrationsfunktionen
- Optimierungsfunktionen
- Fourier-Transformationsfunktionen
- Signal Processing Functions
- Linear Algebra
- Sparse Eigenwerte
- Spatial Data Structures and Algorithms
- Multidimensional Image Processing Functions
- File IO
So let’s get started. 🙂
SciPy ist eine Open-Source-Python-Bibliothek, die zur Lösung wissenschaftlicher und mathematischer Probleme verwendet wird. Sie baut auf der NumPy-Erweiterung auf und ermöglicht es dem Benutzer, Daten mit einer breiten Palette von High-Level-Befehlen zu manipulieren und zu visualisieren. Wie bereits erwähnt, baut SciPy auf NumPy auf. Wenn Sie also SciPy importieren, müssen Sie nicht unbedingt auch NumPy importieren.
NumPy vs SciPy
Beide, NumPy und SciPy, sind Python-Bibliotheken, die für mathematische und numerische Analysen verwendet werden. NumPy enthält Array-Daten und grundlegende Operationen wie Sortierung, Indizierung usw., während SciPy aus dem gesamten numerischen Code besteht. Obwohl NumPy eine Reihe von Funktionen zur Verfügung stellt, die bei der Lösung von linearer Algebra, Fourier-Transformationen usw. helfen können, ist SciPy die Bibliothek, die tatsächlich voll funktionsfähige Versionen dieser Funktionen zusammen mit vielen anderen enthält. Wenn Sie jedoch wissenschaftliche Analysen mit Python durchführen, müssen Sie sowohl NumPy als auch SciPy installieren, da SciPy auf NumPy aufbaut.
Unterpakete in SciPy:
SciPy hat eine Reihe von Unterpaketen für verschiedene wissenschaftliche Berechnungen, die in der folgenden Tabelle aufgeführt sind:

Für eine detaillierte Beschreibung können Sie jedoch der offiziellen Dokumentation folgen.
Diese Pakete müssen vor ihrer Verwendung ausschließlich importiert werden. Zum Beispiel:
from scipy import cluster
Bevor wir uns jede dieser Funktionen im Detail ansehen, lassen Sie uns zuerst einen Blick auf die Funktionen werfen, die sowohl in NumPy als auch in SciPy vorkommen.
Interaktion mit NumPy:
SciPy baut auf NumPy auf und daher können Sie die NumPy-Funktionen selbst nutzen, um Arrays zu behandeln. Um mehr über diese Funktionen zu erfahren, können Sie einfach die Funktionen help(), info() oder source() verwenden.
help():
Um Informationen über eine Funktion zu erhalten, können Sie die Funktion help() verwenden. Es gibt zwei Möglichkeiten, diese Funktion zu verwenden:
- ohne Parameter
- mit Parametern
Das folgende Beispiel zeigt beide Methoden:
from scipy import cluster
help(cluster) #with parameter
help() #without parameter
Wenn Sie den obigen Code ausführen, gibt die erste help() die Informationen über das Cluster-Submodul zurück. Die zweite help() fordert den Benutzer auf, den Namen eines beliebigen Moduls, Schlüsselworts usw. einzugeben, zu dem er Informationen wünscht. Um die Ausführung dieser Funktion zu beenden, geben Sie einfach ‚quit‘ ein und drücken Sie die Eingabetaste.
info():
Diese Funktion gibt Informationen über die gewünschten Funktionen, Module usw. zurück.
scipy.info(cluster)
source():
Der Quellcode wird nur für in Python geschriebene Objekte zurückgegeben. Diese Funktion gibt keine nützlichen Informationen zurück, wenn die Methoden oder Objekte in einer anderen Sprache wie z.B. C geschrieben sind. Falls Sie diese Funktion jedoch nutzen wollen, können Sie dies wie folgt tun:
scipy.source(cluster)
Spezialfunktionen:
SciPy bietet eine Reihe von Spezialfunktionen, die in der mathematischen Physik verwendet werden, wie z.B. elliptische Funktionen, Komfortfunktionen, Gamma, Beta, usw. Um alle Funktionen zu finden, können Sie die Funktion help() verwenden, wie bereits beschrieben.
Exponentielle und trigonometrische Funktionen:
SciPy’s Special Function Paket bietet eine Reihe von Funktionen, mit denen Sie Exponenten finden und trigonometrische Probleme lösen können.
Betrachten Sie das folgende Beispiel:
BEISPIEL:
from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)
Ausgabe:
1000.0
8.0
1.0
0.7071067811865475
Es gibt noch viele andere Funktionen im speziellen Funktionspaket von SciPy, die man selbst ausprobieren kann.
Integrationsfunktionen:
SciPy bietet eine Reihe von Funktionen zur Lösung von Integralen. Vom gewöhnlichen Differentialintegrator bis zur Verwendung von Trapezregeln zur Berechnung von Integralen ist SciPy ein Lagerhaus von Funktionen, um alle Arten von Integralproblemen zu lösen.
Allgemeine Integration:
SiPy bietet eine Funktion namens quad, um das Integral einer Funktion zu berechnen, die eine Variable hat. Die Grenzen können ( ) sein, um unendliche Grenzen anzuzeigen. Die Syntax der Funktion quad() ist wie folgt:
SYNTAX:
quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)
Hier wird die Funktion zwischen den Grenzen a und b integriert (kann auch unendlich sein).
BEISPIEL:
from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)
Im obigen Beispiel wird die Funktion ‚a‘ zwischen den Grenzen 0, 1 ausgewertet. Wenn dieser Code ausgeführt wird, sehen Sie die folgende Ausgabe.
Ausgabe:
(3.9086503371292665, 4.3394735994897923e-14)
Doppelintegralfunktion:
SciPy stellt dblquad zur Verfügung, mit dem man Doppelintegrale berechnen kann. Ein Doppelintegral besteht, wie viele von uns wissen, aus zwei reellen Variablen. Die Funktion dblquad() nimmt die zu integrierende Funktion als Parameter zusammen mit 4 anderen Variablen, die die Grenzen und die Funktionen dy und dx definieren.
BEISPIEL:
from scipy import integrate
a = lambda y, x: x*y**2
b = lambda x: 1
c = lambda x: -1
integrate.dblquad(a, 0, 2, b, c)
AUSGABE:
-1.3333333333333335, 1.4802973661668755e-14)
SciPy bietet verschiedene andere Funktionen zur Auswertung von Dreifachintegralen, n-Integralen, Romberg-Integralen usw., die Sie im Detail erkunden können. Um alle Details über die benötigten Funktionen zu finden, verwenden Sie die Hilfefunktion.
Optimierungsfunktionen:
Die scipy.optimize bietet eine Reihe von häufig verwendeten Optimierungsalgorithmen, die mit der Hilfefunktion eingesehen werden können.
Es besteht im Wesentlichen aus den folgenden:
- Ungebundene und gebundene Minimierung von multivariaten skalaren Funktionen, d.h. minimieren (z.B. BFGS, Newton Conjugate Gradient, Nelder_mead simplex, etc)
- Globale Optimierungsroutinen (z.B.. differential_evolution, dual_annealing, etc)
- Kleinste-Quadrate-Minimierung und Kurvenanpassung (z.B. least_squares, curve_fit, etc)
- Skalare univariate Funktionen, Minimierer und Wurzelfinder (z.B. minimize_scalar und root_scalar)
- Multivariate Gleichungssystemlöser unter Verwendung von Algorithmen wie Hybrid Powell, Levenberg-Marquardt.
Rosenbrook-Funktion:
Die Rosenbrook-Funktion ( rosen) ist ein Testproblem, das für gradientenbasierte Optimierungsalgorithmen verwendet wird. Sie ist in SciPy wie folgt definiert:

BEISPIEL:
import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)
OUTPUT: 7371.0399999999945
Nelder-Mead:
Die Nelder-Mead-Methode ist eine numerische Methode, die häufig verwendet wird, um das Minimum/Maximum einer Funktion in einem mehrdimensionalen Raum zu finden. Im folgenden Beispiel wird die Minimieren-Methode zusammen mit dem Nelder-Mead-Algorithmus verwendet.
BEISPIEL:
from scipy import optimize
a =
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x
AUSGABE: array()
Interpolationsfunktionen:
Im Bereich der numerischen Analyse bezieht sich die Interpolation auf die Konstruktion neuer Datenpunkte innerhalb einer Menge bekannter Datenpunkte. Die SciPy-Bibliothek besteht aus einem Unterpaket namens scipy.interpolate, das Spline-Funktionen und -Klassen, eindimensionale und mehrdimensionale (univariate und multivariate) Interpolationsklassen usw. enthält.
Univariate Interpolation:
Univariate Interpolation ist im Grunde ein Bereich der Kurvenanpassung, der die Kurve findet, die eine exakte Anpassung an eine Reihe von zweidimensionalen Datenpunkten liefert. SciPy bietet die Funktion interp1d, die zur Erstellung einer univariaten Interpolation verwendet werden kann.
BEISPIEL:
import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()
AUSGABE:
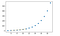
Multivariate Interpolation:
Multivariate Interpolation (räumliche Interpolation ) ist eine Art Interpolation auf Funktionen, die aus mehr als einer Variablen bestehen. Das folgende Beispiel demonstriert ein Beispiel für die
Interpolation über ein 2-D-Gitter unter Verwendung der Funktion interp2d(x, y, z) verwendet grundsätzlich x, y, z-Arrays, um eine Funktion interp2d-Funktion zu approximieren. f: „z = f(x, y)“ und gibt eine Funktion zurück, deren Aufrufmethode Spline-Interpolation verwendet, um den Wert der neuen Punkte zu finden.
BEISPIEL:
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()
AUSGABE:

Fourier-Transformationsfunktionen:
Die Fourier-Analyse ist eine Methode, die sich damit befasst, eine Funktion als Summe periodischer Komponenten auszudrücken und das Signal aus diesen Komponenten wiederherzustellen. Die fft-Funktionen können verwendet werden, um die diskrete Fourier-Transformation einer reellen oder komplexen Sequenz zurückzugeben.
BEISPIEL:
from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)
AUSGABE:
In ähnlicher Weise kann man die Inverse davon finden, indem man die ifft-Funktion wie folgt verwendet:
BEISPIEL:
rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)
AUSGABE:
Signalverarbeitungsfunktionen:
Die Signalverarbeitung befasst sich mit der Analyse, Modifikation und Synthese von Signalen wie Ton, Bildern usw. SciPy bietet einige Funktionen, mit denen man ein- und zweidimensionale Daten entwerfen, filtern und interpolieren kann.
Filtern:
Durch das Filtern eines Signals entfernt man im Grunde genommen unerwünschte Komponenten aus ihm. Um eine geordnete Filterung durchzuführen, können Sie die Funktion order_filter verwenden. Diese Funktion führt grundsätzlich eine geordnete Filterung eines Arrays durch. Die Syntax dieser Funktion lautet wie folgt:
SYNTAX:
order_filter(a, domain, rank)
a = N-dimensionales Eingabe-Array
domain = Masken-Array mit der gleichen Anzahl von Dimensionen wie `a`
rank = Nicht-negative Zahl, die Elemente aus der Liste auswählt, nachdem sie sortiert wurde (0 ist die kleinste, gefolgt von 1…)
BEISPIEL:
from scipy import signal
x = np.arange(35).reshape(7, 5)
domain = np.identity(3)
print(x,end='nn')
print(signal.order_filter(x, domain, 1))
OUTPUT:
]
]
Waveforms:
Das scipy.Signal-Unterpaket besteht auch aus verschiedenen Funktionen, die zur Erzeugung von Wellenformen verwendet werden können. Eine solche Funktion ist chirp. Diese Funktion ist ein frequenzgesteuerter Kosinusgenerator und die Syntax lautet wie folgt:
SYNTAX:
chirp(t, f0, t1, f1, method=’linear‘, phi=0, vertex_zero=True)
wobei,

from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()
OUTPUT:

Lineare Algebra:
Lineare Algebra beschäftigt sich mit linearen Gleichungen und deren Darstellungen mit Hilfe von Vektorräumen und Matrizen. SciPy basiert auf den ATLAS LAPACK- und BLAS-Bibliotheken und ist extrem schnell bei der Lösung von Problemen im Zusammenhang mit linearer Algebra. Zusätzlich zu allen Funktionen von numpy.linalg bietet scipy.linalg noch eine Reihe weiterer fortgeschrittener Funktionen. Außerdem ist scipy.linalg schneller als numpy.linalg, wenn numpy.linalg nicht zusammen mit ATLAS LAPACK- und BLAS-Unterstützung verwendet wird.
Finden der Inversen einer Matrix:
Mathematisch gesehen ist die Inverse einer Matrix A die Matrix, bei der die Identitätsmatrix aus Einsen entlang der Hauptdiagonale besteht, bezeichnet als B=A-1. In SciPy kann diese Inverse mit der Methode linalg.inv ermittelt werden.
BEISPIEL:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)
AUSGABE:
]
Finden der Determinanten:
Der Wert, der sich arithmetisch aus den Koeffizienten der Matrix ergibt, wird als Determinante einer quadratischen Matrix bezeichnet. In SciPy kann dies mit einer Funktion det erfolgen, die folgende Syntax hat:
SYNTAX:
det(a, overwrite_a=False, check_finite=True)
wobei,
a : (M, M) Ist eine quadratische Matrix
overwrite_a( bool, optional) : Erlaubt das Überschreiben von Daten in a
check_finite ( bool, optional): Prüfen, ob die Eingabematrix nur aus endlichen Zahlen besteht
BEISPIEL:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)
AUSGABE: -5.0
Sparse Eigenwerte:
Eigenwerte sind eine bestimmte Menge von Skalaren, die mit linearen Gleichungen verbunden sind. ARPACK bietet die Möglichkeit, Eigenwerte (Eigenvektoren) sehr schnell zu finden. Die gesamte Funktionalität von ARPACK ist in zwei High-Level-Schnittstellen verpackt, nämlich scipy.sparse.linalg.eigs und scipy.sparse.linalg.eigsh. eigs. Die eigs-Schnittstelle erlaubt es, die Eigenwerte reeller oder komplexer unsymmetrischer quadratischer Matrizen zu finden, während die eigsh-Schnittstelle Schnittstellen für reell-symmetrische oder komplex-hermitische Matrizen enthält.
Die Funktion eigs löst ein verallgemeinertes Eigenwertproblem für eine komplexe hermitische oder reell-symmetrische Matrix.
BEISPIEL:
from scipy.linalg import eigh
import numpy as np
A = np.array(, , , ])
a, b = eigh(A)
print("Selected eigenvalues :", a)
print("Complex ndarray :", b)
AUSGABE:
Ausgewählte Eigenwerte :
Komplexes ndarray :
]
Räumliche Datenstrukturen und Algorithmen:
Räumliche Daten bestehen grundsätzlich aus Objekten, die aus Linien, Punkten, Flächen usw. bestehen. Das scipy.spatial-Paket von SciPy kann Voronoi-Diagramme, Triangulationen usw. mit Hilfe der Qhull-Bibliothek berechnen. Es besteht auch aus KDTree-Implementierungen für die Abfrage nächstgelegener Punkte.
Delaunay-Triangulationen:
Mathematisch gesehen ist eine Delaunay-Triangulation für eine Menge diskreter Punkte in einer Ebene eine Triangulation, bei der kein Punkt der gegebenen Menge von Punkten innerhalb des Umkreises eines beliebigen Dreiecks liegt.
BEISPIEL:
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()
AUSGABE:

Mehrdimensionale Bildverarbeitungsfunktionen:
Bildverarbeitung befasst sich im Wesentlichen mit der Durchführung von Operationen an einem Bild, um Informationen abzurufen oder ein verbessertes Bild aus dem Original zu erhalten. Das Paket scipy.ndimage besteht aus einer Reihe von Bildverarbeitungs- und Analysefunktionen, die für die Arbeit mit Arrays beliebiger Dimensionalität entwickelt wurden.
Faltung und Korrelation:
SciPy bietet eine Reihe von Funktionen, die Korrelation und Faltung von Bildern ermöglichen.
- Die Funktion correlate1d kann verwendet werden, um eine eindimensionale Korrelation entlang einer gegebenen Achse zu berechnen
- Die Funktion correlate ermöglicht eine mehrdimensionale Korrelation eines beliebigen Arrays mit dem angegebenen Kernel
- Die Funktion convolve1d kann verwendet werden, um eine eindimensionaledimensionalen Faltung entlang einer gegebenen Achse
- Die Funktion convolve ermöglicht die mehrdimensionale Faltung eines beliebigen Arrays mit dem angegebenen Kernel
BEISPIEL:
import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)
AUSGABE: array()
File IO:
Das scipy.io-Paket bietet eine Reihe von Funktionen, die Ihnen helfen, Dateien verschiedener Formate wie MATLAB-Dateien, IDL-Dateien, Matrix Market-Dateien usw. zu verwalten.
Um dieses Paket zu nutzen, müssen Sie es wie folgt importieren:
import scipy.io as sio
Für vollständige Informationen über das Unterpaket können Sie das offizielle Dokument über File IO lesen.
Damit sind wir am Ende dieses SciPy-Tutorials. Ich hoffe, du hast alles gut verstanden. Stellen Sie sicher, dass Sie so viel wie möglich üben.
Wenn Sie mehr Artikel über die aktuellsten Technologien wie Künstliche Intelligenz, DevOps, Ethical Hacking lesen möchten, dann können Sie sich auf die offizielle Seite von Edureka beziehen.
Halten Sie Ausschau nach anderen Artikeln in dieser Serie, die verschiedene andere Aspekte von Python und Data Science erklären werden.
1. Machine Learning Classifier in Python
2. Python Scikit-Learn Cheat Sheet
3. Machine Learning Tools
4. Python Libraries For Data Science And Machine Learning
5. Chatbot in Python
6. Python Collections
7. Python Module
8. Python Entwickler Fähigkeiten
9. OOPs Interview Fragen und Antworten
10. Lebenslauf für einen Python-Entwickler
11. Explorative Datenanalyse in Python
12. Schlangenspiel mit Pythons Schildkrötenmodul
13. Python-Entwickler-Gehalt
14. Principal Component Analysis
15. Python gegen C++
16. Scrapy Tutorial
17. Web Scraping mit Python
18. Regressionsmethode der kleinsten Quadrate
19. Jupyter Notebook Spickzettel
20. Python-Grundlagen
21. Python-Muster-Programme
22. Generatoren in Python
23. Python Dekorator
24. Python Spyder IDE
25. Mobile Anwendungen mit Kivy in Python
26. Top 10 der besten Bücher zum Lernen & Python üben
27. Roboter-Framework mit Python
28. Schlangenspiel in Python mit PyGame
29. Django Interview Fragen und Antworten
30. Top 10 Python Anwendungen
31. Hash-Tabellen und Hashmaps in Python
32. Python 3.8
33. Support-Vektor-Maschine
34. Python Tutorial