Wie man mit Exponenten und Logarithmen denkt

Hier ist ein Trick, um Probleme mit Exponenten und Logarithmen zu durchdenken. Stellen Sie einfach zwei Fragen:

1) Sprechen wir über Inputs (Ursache der Veränderung) oder Outputs (die tatsächliche Veränderung, die stattgefunden hat?)

Logarithmen enthüllen die Inputs, die das Wachstum verursacht haben
Exponenten finden das Endergebnis des Wachstums

2) Sprechen wir über die Perspektive des Erzeugers oder die eines Beobachters?

e und der natürliche Logarithmus sind aus der Perspektive des Züchters von Augenblick zu Augenblick
Base 10, Base 2, etc. sind Messungen, die für einen menschlichen Beobachter geeignet sind

In meinem Kopf stelle ich die Optionen in einer Tabelle zusammen:

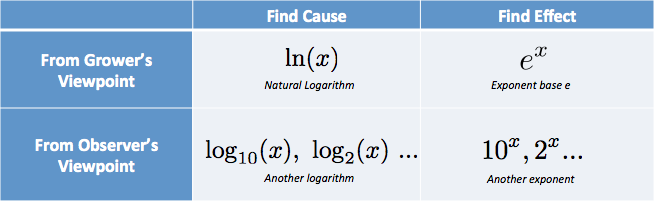
Exponent-Logarithmus-Vergleich

Ich habe Gedanken wie „Ich brauche die Ursache, aus der Perspektive des Züchters… das ist der natürliche Logarithmus.“. (Natürlicher Logarithmus wird mit LN abgekürzt, vom hochtrabenden logarithmus naturalis.)

Ich war frustriert von Klassen, die den inneren Teil der Tabelle beschrieben, die rohen Funktionen, ohne die Beschriftungen, die erklärten, wann sie zu verwenden sind!

Das wird nicht funktionieren, lassen Sie uns direkt üben, mit Logarithmen und Exponenten zu denken.

Szenario: Beschreiben des BIP-Wachstums

Hier ist ein typisches Beispiel für Wachstum:

Von 2000 bis 2010 hat sich das BIP der USA von 9,9 Billionen auf 14,4 Billionen verändert

Ok, sicher, diese Zahlen zeigen, dass Veränderungen stattgefunden haben. Aber wir wollen wahrscheinlich einen Einblick in die Ursache: Welche durchschnittliche jährliche Wachstumsrate ist für diese Veränderung verantwortlich?

Ich denke sofort an „Logarithmen“, denn wir arbeiten uns vom Wachstum rückwärts zu der Rate vor, die es verursacht hat. Ich beginne mit einem Gedanken wie diesem:

$\displaystyle{\text{logarithm of change} \rightarrow \text{Ursache des Wachstums}$

Ein guter Anfang, aber lassen Sie uns das Ganze noch etwas verfeinern:

Erstens, welchen Logarithmus sollten wir verwenden?

Standardmäßig wähle ich den natürlichen Logarithmus. Die meisten Ereignisse beziehen sich auf den Erzeuger (nicht auf den Beobachter), und ich mag es, mit dem wachsenden Element „mitzufahren“, um zu visualisieren, was passiert. (Radianten sind ähnlich: sie messen Winkel in Bezug auf den Beweger.)

Nächste Frage: auf welche Veränderung wenden wir den Logarithmus an?

Wir sind eigentlich nur an dem Verhältnis zwischen Anfang und Ende interessiert: 9,9 Billionen zu 14,4 Billionen in 10 Jahren. Das ist die gleiche Wachstumsrate, wie wenn man im gleichen Zeitraum von 9,90 $ auf 14,40 $ steigt.

Wir können unseren Gedankengang schärfen:

$\displaystyle{\text{natürlicher Logarithmus des Wachstumsverhältnisses} \rightarrow \text{Ursache des Wachstums} }$

$\displaystyle{\ln(\frac{14.4}{9.9}) = .374}$

Ok, die Ursache war eine Rate von .374 oder 37,4%. Sind wir fertig?

Noch nicht. Logarithmen wissen nicht, wie lange eine Veränderung gedauert hat (wir haben keine 10 Jahre eingesetzt, richtig?). Sie geben eine Rate an, als ob die gesamte Veränderung in einem einzigen Zeitraum stattgefunden hätte.

Die Veränderung könnte in der Tat ein einziges Jahr mit einem kontinuierlichen Wachstum von 37,4 % sein, oder zwei Jahre mit einem Wachstum von 18,7 %, oder eine andere Kombination.

Aus dem Szenario wissen wir, dass die Veränderung 10 Jahre dauerte, also muss die Rate folgendermaßen gewesen sein:

$\displaystyle{ \text{rate} = \frac{.374}{10} = .0374 = 3.74\%}$

Aus der Sicht eines sofortigen, kontinuierlichen Wachstums wuchs die US-Wirtschaft um 3.74% pro Jahr.

Sind wir jetzt fertig? Nicht ganz!

Diese kontinuierliche Rate ist aus der Sicht des Wachsenden, als ob wir mit der Wirtschaft „mitfahren“, während sie sich verändert. Ein Banker interessiert sich wahrscheinlich für die menschenfreundliche Differenz von Jahr zu Jahr. Wir können dies herausfinden, indem wir das kontinuierliche Wachstum ein Jahr lang laufen lassen:

$\displaystyle{\text{exponent with rate and time} \rightarrow \text{Auswirkung des Wachstums} }$

$\displaystyle{e^{\text{rate} \cdot \text{time}} = \text{growth}}$

$\displaystyle{e^{.0374 \cdot 1} = 1.0381}$

Der Zuwachs gegenüber dem Vorjahr beträgt 3,8 % und ist damit etwas höher als die momentane Rate von 3,74 % aufgrund der Zinseszinsen. Man kann es auch anders ausdrücken:

Aktuell gesehen wächst ein bestimmter Teil der Wirtschaft um 3,74%, modelliert durch $e^(.0374 * Jahre)$
Auf Jahresbasis, unter Berücksichtigung von Aufzinsungseffekten, wächst die Wirtschaft um 3,81%, modelliert durch $1,0381^Jahre$

In der Finanzwelt wollen wir vielleicht die Veränderung von Jahr zu Jahr, die sich gut mit anderen Trends vergleichen lässt. In Wissenschaft und Technik ziehen wir es vor, das Verhalten auf einer momentanen Basis zu modellieren.

Szenario: Beschreibung des natürlichen Wachstums

Ich verabscheue konstruierte Beispiele wie „Nehmen wir an, dass sich Bakterien alle 24 Stunden verdoppeln, dann finden Sie ihre Wachstumsformel.“. Vermehren sich Bakterienkolonien in sauberen menschlichen Intervallen, und warten wir auf eine exakte Verdopplung?

Ein besseres Szenario: „Hey, ich habe ein paar Bakterien gefunden, eine Stunde gewartet, und der Klumpen ist von 2,3 Gramm auf 2,32 Gramm gewachsen. Ich gehe jetzt zum Mittagessen. Rechne aus, wie viel wir haben werden, wenn ich in 3 Stunden zurück bin.“

Lassen Sie uns das modellieren. Wir brauchen einen Logarithmus, um die Wachstumsrate zu ermitteln, und dann einen Exponenten, um dieses Wachstum in die Zukunft zu projizieren. Wie zuvor behalten wir alles in Form des natürlichen Logarithmus bei.

Der Wachstumsfaktor ist:

$\displaystyle{\text{logarithm of change} \rightarrow \text{Ursache des Wachstums} }$

$\displaystyle{\ln(\text{Wachstum})) = \ln(2.32/2.3) = .0086 = .86\%}$

Das ist die Rate für eine Stunde, und das allgemeine Modell zur Projektion in die Zukunft lautet

$\displaystyle{\text{Exponent mit Rate und Zeit} \rightarrow \text{Auswirkung des Wachstums} }$

$\displaystyle{e^{.0086 \cdot \text{Stunden}} \rightarrow \text{effekt des wachstums} }$

Wenn wir mit 2,32 beginnen und 3 Stunden lang wachsen, haben wir:

$\displaystyle{2,32 \cdot e^{.0086 \cdot 3} = 2,38}$

Nur zum Spaß: Wie lange dauert es, bis sich die Bakterien verdoppeln? Stellen Sie sich vor, Sie warten darauf, dass aus 1 2 wird:

$\displaystyle{1 \cdot e^{.0086 \cdot \text{hours}} = 2}$

Wir können mechanisch den natürlichen Logarithmus beider Seiten nehmen, um „den Exponenten rückgängig zu machen“, aber lassen Sie uns intuitiv denken.

Wenn 2 das Endergebnis ist, dann ist ln(2) der Wachstumsinput, der uns dorthin gebracht hat (eine Rate × Zeit). Wir wissen, dass die Rate 0,0086 war, also wäre die Zeit, um 2 zu erreichen:

$\displaystyle{ \text{hours} = \frac{\ln(2)}{\text{rate}} = \frac{.693}{.0086} = 80.58}$

Die Kolonie wird sich nach ~80 Stunden verdoppeln. (Gut, dass du nicht geblieben bist?)

Was bedeutet der Perspektivenwechsel wirklich?

Herauszufinden, ob man den Input (Ursache des Wachstums) oder den Output (Ergebnis des Wachstums) will, ist ziemlich einfach. Aber wie veranschaulicht man die Perspektive des Züchters?

Stellen Sie sich vor, wir haben kleine Arbeiter, die das endgültige Wachstumsmuster aufbauen (siehe den Artikel über Exponenten):

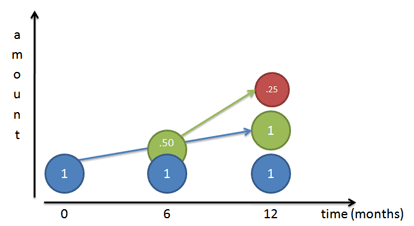
$Zinseszins$

Wenn unsere Wachstumsrate 100 % beträgt, sagen wir unserem anfänglichen Arbeiter (Mr. Blue), dass er stetig arbeiten und bis zum Ende des Jahres eine 100 %ige Kopie von sich selbst schaffen soll. Wenn wir ihn Tag für Tag verfolgen, sehen wir, dass er am Ende des Jahres eine 100%ige Kopie von sich selbst (Herr Grün) fertigstellt.

Aber… der Arbeiter, den er gebaut hat (Herr Grün), beginnt auch zu arbeiten. Wenn Herr Grün zum ersten Mal an der 6-Monats-Marke auftaucht, hat er ein halbes Jahr Zeit zu arbeiten (dieselbe Jahresrate wie Herr Blau) und er baut Herrn Rot. Natürlich ist Herr Rot am Ende nur halb fertig, da Herr Grün nur 6 Monate Zeit hat.

Was wäre, wenn Herr Grün nach 4 Monaten auftaucht? Einem Monat? Einem Tag? Eine Sekunde? Wenn die Arbeiter sofort zu wachsen beginnen, erhalten wir die durch $e^x$ definierte Kurve:

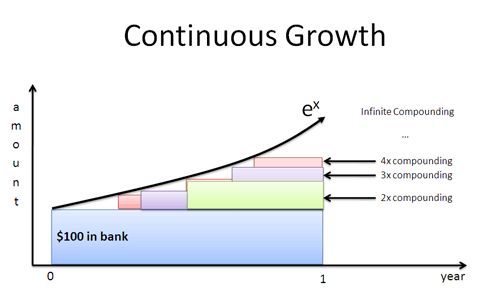
Kontinuierliches Wachstum

Der natürliche Logarithmus ergibt eine Wachstumsrate aus der Sicht eines einzelnen Arbeiters. Wir setzen diese Rate in $e^x$ ein, um das Endergebnis zu erhalten, einschließlich aller Aufzinsungen.

Verwendung anderer Basen

Wenn wir zu einer anderen Art von Logarithmus (zur Basis 10, zur Basis 2 usw.) wechseln, suchen wir nach einem Muster im Gesamtwachstum, nicht nach dem, was der einzelne Arbeitnehmer tut.

Jeder Logarithmus stellt eine Frage, wenn er eine Veränderung sieht:

Log Basis e: Wie hoch war die momentane Rate, die jeder Arbeiter eingehalten hat?
Log Basis 2: Wie viele Verdoppelungen waren erforderlich?
Log Basis 10: Wie viele Verzehnfachungen waren erforderlich?

Hier ist ein zu analysierendes Szenario:

Im Laufe von 30 Jahren stieg die Anzahl der Transistoren auf typischen Chips von 1000 auf 1 Milliarde

Wie würden Sie das analysieren?

Mikrochips sind keine einheitliche Einheit, die im Laufe der Zeit gleichmäßig wächst. Sie sind separate Ausgaben von konkurrierenden Unternehmen und zeigen einen allgemeinen Techniktrend an.
Da wir nicht mit einem expandierenden Mikrochip „mitfahren“, sollten wir einen Maßstab verwenden, der der menschlichen Bequemlichkeit dient. Eine Verdopplung ist einfacher zu denken als eine Verzehnfachung.

Mit diesen Annahmen erhalten wir:

$\displaystyle{\text{logarithm of change} \rightarrow \text{Ursache des Wachstums} }$

$\displaystyle{\log_2(\frac{\text{1 Milliarde}}{1000}) = \log_2(\text{1 Million}) \sim \text{20 Verdoppelungen}}$

Die „Ursache des Wachstums“ waren 20 Verdoppelungen, von denen wir wissen, dass sie in 30 Jahren stattfanden. Das sind im Durchschnitt 2/3 Verdopplungen pro Jahr oder 1,5 Jahre pro Verdopplung – eine gute Faustregel.

Aus der Sicht des Züchters würden wir $\ln(\text{1 Milliarde}/1000) / \text{30 Jahre} = 46\%$ kontinuierliches Wachstum berechnen (was in diesem Szenario etwas schwieriger zu verstehen ist).

Wir können unsere Analyse in einer Tabelle zusammenfassen:

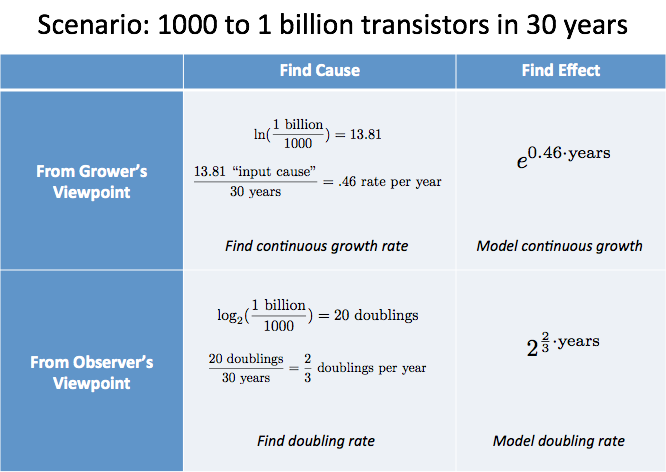
Exponenten Transistorbeispiel

Zusammenfassung

Beim Lernen geht es darum, die versteckten Bezeichnungen hinter einem Konzept zu finden. Wann wird er verwendet? Welche Sichtweise bringt er in das Problem ein?

Meine derzeitige Interpretation ist, dass Exponenten nach Ursache und Wirkung und Erzeuger und Beobachter fragen. Aber wir sind nie fertig; ein Teil des Spaßes besteht darin, zu sehen, wie wir alte Konzepte wieder aufgreifen können.

Glücklich mit Mathe.

Anhang: Die Formel für den Wechsel der Basis

Hier ist, wie man über den Wechsel der Basis nachdenkt. Unter der Annahme einer kontinuierlichen Wachstumsrate von 100 %

ln(x) ist die Zeit, um auf x zu wachsen
ln(2) ist die Zeit, um auf 2 zu wachsen

Da wir die Zeit haben, um uns zu verdoppeln, können wir sehen, wie viele in die Gesamtzeit, um auf x zu wachsen, „passen“ würden:

$\displaystyle{\text{Anzahl der Verdoppelungen von 1 bis x} = \frac{\ln(x)}{\ln(2)} = \log_2(x)}$

Wie viele Verdoppelungen gibt es zum Beispiel von 1 bis 64?

Nun, ln(64) = 4,158. Und ln(2) = 0,693. Die Anzahl der passenden Verdoppelungen ist:

$\displaystyle{\frac{\ln(64)}{\ln(2)} = \frac{4.158}{.693} = 6}$

In der realen Welt können Taschenrechner an Präzision verlieren, also verwenden Sie möglichst eine direkte Logarithmusfunktion zur Basis 2. Und natürlich können wir eine gebrochene Zahl haben: Von 1 auf die Quadratwurzel aus 2 zu kommen, ist eine „halbe“ Verdoppelung, oder log2(1,414) = 0,5.

Der Wechsel zur logarithmischen Basis 10 bedeutet, dass wir die Anzahl der 10x-ings zählen, die passen:

$\displaystyle{\text{Anzahl der 10x-ings von 1 bis x} = \frac{\ln(x)}{\ln(10)} = \log_{10}(x) }$

Niedlich, oder? Weitere Beispiele findest du unter Verwendung von Logarithmen in der realen Welt.