Fórmulas Pi

Posted on by admin
Teoría de números > Constantes > Pi >
Cálculo y análisis > Series > Fórmulas BBP >
Cálculo y análisis > Cálculo > Integrales > Integrales definidas >
MathWorld Colaboradores > Cloitre >
MathWorld Colaboradores > Plouffe >
MathWorld Colaboradores > Sondow >

Menos…

Descárgate el Cuaderno de Mathematica

Hay muchas fórmulas de pi de muchos tipos. Entre otras, incluyen series, productos, construcciones geométricas, límites, valores especiales e iteraciones de pi.

pi está íntimamente relacionada con las propiedades de los círculos y las esferas. Para un círculo de radio r, la circunferencia y el área vienen dadas por

C = 2pir
(1)
A = pir^2.
(2)

De forma similar, para una esfera de radio r, la superficie y el volumen encerrados son

S = 4pir^2
(3)
V = 4/3pir^3.
(4)

Una fórmula exacta para pi en términos de las tangentes inversas de fracciones unitarias es la fórmula de Machin

1/4pi=4tan^(-1)(1/5)-tan^(-1)(1/(239)).
(5)

Hay otras tres fórmulas similares a la de Machin, así como miles de otras fórmulas similares que tienen más términos.

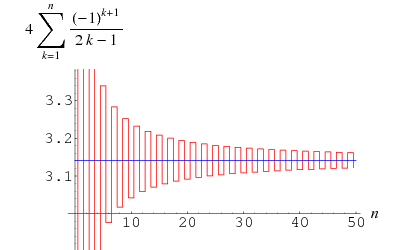
GregorySeries

Gregory y Leibniz encontraron

pi/4 = suma_(k=1)^(infty)((-1)^(k+1))/(2k-1)
(6)
= 1-1/3+1/5-...
(7)

(Wells 1986, p. 50), que se conoce como la serie de Gregory y puede obtenerse insertando x=1 en la serie de Leibniz para tan^(-1)x. ¡El error después del nésimo término de esta serie en la serie de Gregory es mayor que (2n)^(-1) por lo que esta suma converge tan lentamente que 300 términos no son suficientes para calcular pi correctamente con dos decimales! Sin embargo, se puede transformar en

pi=suma_(k=1)^infty(3^k-1)/(4^k)zeta(k+1),
(8)

donde zeta(z) es la función zeta de Riemann (Vardi 1991, pp. 157-158; Flajolet y Vardi 1996), de modo que el error después de k términos es aproximadamente (3/4)^k.

Una serie de suma infinita a Abraham Sharp (ca. 1717) viene dada por

pi=suma_(k=0)^infty(2(-1)^k3^(1/2-k))/(2k+1)
(9)

(Smith 1953, p. 311). Otras series simples en las que aparece pi son

1/(2-3-4)-1/(4-5-6)+1/(6-7-8)-…

1/4pisqrt(2) = suma_(k=1)^(infty)
(10)
= 1+1/3-1/5-1/7+1/9+1/(11)-...
(11)
1/4(pi-3) = suma_(k=1)^(infty)((-1)^(k+1))/(2k(2k+1)(2k+2))
(12)
=
(13)
1/6pi^2 = suma_(k=1)^(infty)1/(k^2)
(14)
= 1+1/4+1/9+1/(16)+1/(25)+...
(15)
1/8pi^2 = suma_(k=1)^(infty)1/((2k-1)^2)
(16)
= 1+1/(3^2)+1/(5^2)+1/(7^2)+...
(17)

(Wells 1986, p. 53).

En 1666, Newton utilizó una construcción geométrica para derivar la fórmula

pi = 3/4sqrt(3)+24int_0^(1/4)sqrt(x-x^2)dx
(18)
= (3sqrt(3))/4+24(1/(12)-1/(5-2^5)-1/(28-2^7)-1/(72-2^9)-...),
(19)

que utilizó para calcular pi (Wells 1986, p. 50; Borwein et al. 1989; Borwein y Bailey 2003, pp. 105-106). Los coeficientes se pueden encontrar a partir de la integral

I(x) = intsqrt(x-x^2)dx
(20)
= 1/4(2x-1)sqrt(x-x^2)-1/8sin^(-1)(1-2x)
(21)

tomando la expansión en serie de I(x)-I(0) sobre 0, obtaining

I(x)=2/3x^(3/2)-1/5x^(5/2)-1/(28)x^(7/2)-1/(72)x^(9/2)-5/(704)x^(11/2)+...
(22)

(OEIS A054387 y A054388). Utilizando la transformación de mejora de la convergencia de Euler se obtiene

pi/2 = 1/2suma_(n=0)^(infty)((n!)^22^(n+1))/((2n+1)!)=suma_(n=0)^(infty)(n!)/((2n+1)!)
(23)
= 1+1/3+(1-2)/(3-5)+(1-2-3)/(3-5-7)+...
(24)
= 1+1/3(1+2/5(1+3/7(1+4/9(1+...))))
(25)

(Beeler et al. 1972, Tema 120).

Esto corresponde a enchufar x=1/cuadrado(2) en la serie de potencias de la función hipergeométrica _2F_1(a,b;c;x),

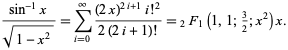(sin^(-1)x)/(sqrt(1-x^2))=sum_(i=0)^infty((2x)^(2i+1)i!^2)/(2(2i+1)!)=_2F_1(1,1;3/2;x^2)x.
(26)

A pesar de la mejora de la convergencia, la serie (◇) converge sólo a un bit/término. ¡A costa de una raíz cuadrada, Gosper ha observado que x=1/2 da 2 bits/término,

1/9sqrt(3)pi=1/2sum_(i=0)^infty((i!)^2)/((2i+1)!),
(27)

y x=sin(pi/10) da casi 3.39 bits/término,

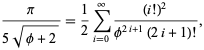pi/(5sqrt(phi+2))=1/2sum_(i=0)^infty((i!)^2)/(phi^(2i+1)(2i+1)!),
(28)

donde phi es la proporción áurea. Gosper también obtuvo

pi=3+1/(60)(8+(2-3)/(7-8-3)(13+(3-5)/(10-11-3)(18+(4-7)/(13-14-3)(23+...)))).
(29)

Un algoritmo de espiga para pi es dado por Rabinowitz y Wagon (1995; Borwein y Bailey 2003, pp. 141-142).

Más sorprendente aún, una expresión de forma cerrada que da un algoritmo de extracción de dígitos que produce dígitos de pi (o pi^2) en base-16 fue descubierta por Bailey et al. (Bailey et al. 1997, Adamchik y Wagon 1997),

pi=suma_(n=0)^infty(4/(8n+1)-2/(8n+4)-1/(8n+5)-1/(8n+6))(1/(16))^n.
(30)

Esta fórmula, conocida como fórmula BBP, fue descubierta utilizando el algoritmo PSLQ (Ferguson et al. 1999) y es equivalente a

pi=int_0^1(16y-16)/(y^4-2y^3+4y-4)dy.
(31)

Hay una serie de fórmulas de tipo BBP para pi en potencias de (-1)^k, cuyas primeras fórmulas independientes son

pi = 4suma_(k=0)^(infty)((-1)^k)/(2k+1)
(32)
= 3suma_(k=0)^(infty)(-1)^k
(33)
= 4suma_(k=0)^(infty)(-1)^k
(34)
= suma_(k=0)^(infty)(-1)^k
(35)
= suma_(k=0)^(infty)(-1)^k
(36)
= suma_(k=0)^(infty)(-1)^k.
(37)

De forma similar, hay una serie de fórmulas de tipo BBP para pi en potencias de 2^k, cuyas primeras fórmulas independientes son

.

1/(96)sum_(k=0)^(infty)1/(4096^k)

pi = suma_(k=0)^(infty)1/(16^k)
(38)
= 1/2suma_(k=0)^(infty)1/(16^k)
(39)
= 1/(16)sum_(k=0)^(infty)1/(256^k)
(40)
= 1/(32)sum_(k=0)^(infty)1/(256^k)
(41)
= 1/(32)sum_(k=0)^(infty)1/(4096^k)
(42)
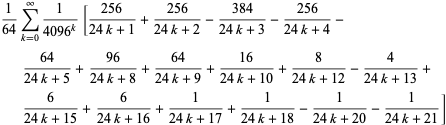= 1/(64)sum_(k=0)^(infty)1/(4096^k)
(43)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(44)
=
(45)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(46)
= 1/(4096)sum_(k=0)^(infty)1/(65536^k)
(47)
= 1/(4096)sum_(k=0)^(infty)1/(65536^k).
(48)

F. Bellard encontró la fórmula de tipo BBP de rápida convergencia

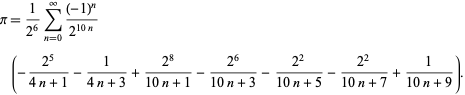pi=1/(2^6)sum_(n=0)^infty((-1)^n)/(2^(10n))(-(2^5)/(4n+1)-1/(4n+3)+(2^8)/(10n+1)-(2^6)/(10n+3)-(2^2)/(10n+5)-(2^2)/(10n+7)+1/(10n+9)).
(49)

Una integral relacionada es

pi=(22)/7-int_0^1(x^4(1-x)^4)/(1+x^2)dx
(50)

(Dalzell 1944, 1971; Le Lionnais 1983, p. 22; Borwein, Bailey y Girgensohn 2004, p. 3; Boros y Moll 2004, p. 125; Lucas 2005; Borwein et al. 2007, p. 14). Esta integral fue conocida por K. Mahler a mediados de la década de 1960 y aparece en un examen de la Universidad de Sidney en noviembre de 1960 (Borwein, Bailey y Girgensohn, p. 3). Beukers (2000) y Boros y Moll (2004, p. 126) afirman que no está claro si existe una elección natural de polinomio racional cuya integral entre 0 y 1 produzca pi-333/106, donde 333/106 es el siguiente convergente. Sin embargo, existe una integral para el cuarto convergente, a saber

pi=(355)/(113)-1/(3164)int_0^1(x^8(1-x)^8(25+816x^2))/(1+x^2)dx.
(51)

(Lucas 2005; Bailey et al. 2007, p. 219). De hecho, Lucas (2005) ofrece otras integrales de este tipo.

Backhouse (1995) utilizó la identidad

I_(m,n) = int_0^1(x^m(1-x)^n)/(1+x^2)dx
(52)
= 2^(-(m+n+1))sqrt(pi)Gamma(m+1)Gamma(n+1)×_3F_2(1,(m+1)/2,(m+2)/2;(m+n+2)/2,(m+n+3)/2;-1)
(53)
= a+bpi+cln2
(54)

para los enteros positivos m y n y donde a, b, y c son constantes racionales para generar una serie de fórmulas para pi. En particular, si 2m-n=0 (mod 4), entonces c=0 (Lucas 2005).

Una fórmula similar fue descubierta posteriormente por Ferguson, lo que lleva a un entramado bidimensional de tales fórmulas que puede ser generado por estas dos fórmulas dadas por

pi=suma_(k=0)^infty((4+8r)/(8k+1)-(8r)/(8k+2)-(4r)/(8k+3)-(2+8r)/(8k+4)-(1+2r)/(8k+5)-(1+2r)/(8k+6)+r/(8k+7))(1/(16))^k
(55)

para cualquier valor complejo de r (Adamchik y Wagon), dando la fórmula BBP como el caso especial r=0.

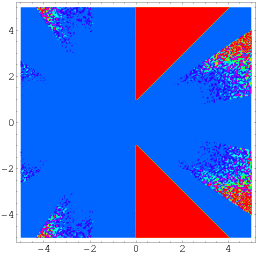
PiFormulasWagonIdentity

Una identidad aún más general debida a Wagon viene dada por

pi+4tan^(-1)z+2ln((1-2z-z^2)/(z^2+1))=suma_(k=0)^infty1/(16^k)
(56)

(Borwein y Bailey 2003, p. 141), que se mantiene sobre una región del plano complejo que excluye dos porciones triangulares colocadas simétricamente alrededor del eje real, como se ilustra arriba.¡

Una clase general de identidades quizás más extraña viene dada por

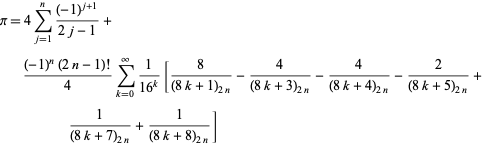pi=4sum_(j=1)^n((-1)^(j+1))/(2j-1)+((-1)^n(2n-1)!)/4suma_(k=0)^infty1/(16^k)
(57)

que se mantiene para cualquier entero positivo n, donde (x)_n es un símbolo de Pochhammer (B. Cloitre, com. pers., 23 de enero de 2005). Y lo que es más sorprendente, existe una fórmula estrechamente análoga para el logaritmo natural de 2.

Tras el descubrimiento de la fórmula BBP de base 16 y las fórmulas relacionadas, se investigaron fórmulas similares en otras bases. Borwein, Bailey y Girgensohn (2004) han demostrado recientemente que pi no tiene una fórmula arctangente BBP de tipo Machin que no sea binaria, aunque esto no descarta un esquema completamente diferente para los algoritmos de extracción de dígitos en otras bases.

S. Plouffe ha ideado un algoritmo para calcular el nésimo dígito de pi en cualquier base en O(n^3(logn)^3) pasos.

Una serie de identidades adicionales debidas a Ramanujan, Catalan y Newton son dadas por Castellanos (1988ab, pp. 86-88), incluyendo varias que implican sumas de números de Fibonacci. Ramanujan encontró

suma_(k=0)^infty((-1)^k(4k+1)^3)/(^3)=suma_(k=0)^infty((-1)^k(4k+1)^3)/(pi^(3/2)^3)=2/pi
(58)

(Hardy 1923, 1924, 1999, p. 7).

Plouffe (2006) encontró la hermosa fórmula

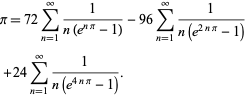pi=72sum_(n=1)^infty1/(n(e^(npi)-1))-96sum_(n=1)^infty1/(n(e^(2npi)-1)) +24sum_(n=1)^infty1/(n(e^(4npi)-1)).
(59)

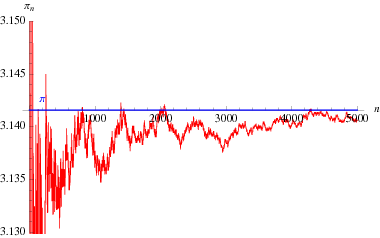
PiBlatnerProduct

Una interesante fórmula del producto infinito debida a Euler que relaciona pi y el nésimo primo p_n es

.

pi = 2/(producto_(n=1)^(infty))
(60)
= 2/(producto_(n=2)^(infty))
(61)

(Blatner 1997, p. 119), graficado arriba como una función del número de términos en el producto.

Un método similar al de Arquímedes puede ser usado para estimar pi comenzando con un n-gón y luego relacionando el área de los subsecuentes 2n-gones. Sea beta el ángulo desde el centro de uno de los segmentos del polígono,

beta=1/4(n-3)pi,
(62)

entonces

pi=(2sin(2beta))/((n-3)producto_(k=0)^(infty)cos(2^(-k)beta))
(63)

(Beckmann 1989, pp. 92-94).

Vieta (1593) fue el primero en dar una expresión exacta para pi tomando n=4 en la expresión anterior, dando

cosbeta=sinbeta=1/(sqrt(2))=1/2sqrt(2),
(64)

lo que lleva a un producto infinito de radicales anidados,

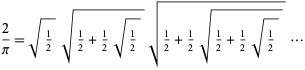2/pi=sqrt(1/2)sqrt(1/2+1/2sqrt(1/2))sqrt(1/2+1/2sqrt(1/2))...
(65)

(Wells 1986, p. 50; Beckmann 1989, p. 95). Sin embargo, no se demostró rigurosamente que esta expresión converge hasta Rudio en 1892.

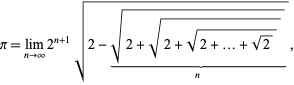
Una fórmula relacionada viene dada por

pi=lim_(n-infty)2^(n+1)sqrt(2-sqrt(2+sqrt(2+sqrt(2+...+sqrt(2))))_()_(n)),
(66)

que puede escribirse

pi=lim_(n-infty)2^(n+1)pi_n,
(67)

donde pi_n se define utilizando la iteración

pi_n=sqrt((1/2pi_(n-1))^2+^2)
(68)

con pi_0=sqrt(2) (J. Munkhammar, com. pers, 27 de abril de 2000). La fórmula

pi=2lim_(m-infty)sum_(n=1)^msqrt(^2+1/(m^2))
(69)

también está muy relacionado.

Una bonita fórmula para pi viene dada por

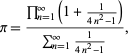pi=(producto_(n=1)^(infty)(1+1/(4n^2-1)))/(suma_(n=1)^(infty)1/(4n^2-1)),
(70)

donde el numerador es una forma de la fórmula de Wallis para pi/2 y el denominador es una suma telescópica con suma 1/2 ya que

1/(4n^2-1)=1/2(1/(2n-1)-1/(2n+1))
(71)

(Sondow 1997).

Un caso particular de la fórmula de Wallis da

pi/2=producto_(n=1)^infty=(2-2)/(1-3)(4-4)/(3-5)(6-6)/(5-7)...
(72)

(Wells 1986, p. 50). Esta fórmula también puede escribirse

lim_(n-infty)(2^(4n))/(n(2n; n)^2)=pilim_(n-infty)(n^2)/(^2)=pi,
(73)

donde (n; k) denota un coeficiente binomial y Gamma(x) es la función gamma (Knopp 1990). Euler obtuvo

pi=sqrt(6(1+1/(2^2)+1/(3^2)+1/(4^2)+...)),
(74)

que se deduce del valor especial de la función zeta de Riemann zeta(2)=pi^2/6. Fórmulas similares se siguen de zeta(2n) para todos los enteros positivos n.

Una suma infinita debida a Ramanujan es

1/pi=sum_(n=0)^infty(2n; n)^3(42n+5)/(2^(12n+4))
(75)

(Borwein et al. 1989; Borwein y Bailey 2003, p. 109; Bailey et al.2007, p. 44). Otras sumas se dan en Ramanujan (1913-14),

4/pi=sum_(n=0)^infty((-1)^n(1123+21460n)(2n-1)!!(4n-1)!)/(882^(2n+1)32^n(n!¡)^3)
(76)

y

1/pi = sqrt(8)sum_(n=0)^(infty)((1103+26390n)(2n-1)!!(4n-1)!!)/(99^(4n+2)32^n(n!)^3)
(77)
= (sqrt(8))/(9801)sum_(n=0)^(infty)((4n)!(1103+26390n))/((n!)^4396^(4n))
(78)

(Beeler et al. 1972, Tema 139; Borwein et al. 1989; Borwein y Bailey 2003, p. 108; Bailey et al. 2007, p. 44). La ecuación (78) se deriva de una identidad modular de orden 58, aunque no se presentó una primera derivación antes de Borwein y Borwein (1987). Las series anteriores dan ambas

pi aprox (9801)/(2206sqrt(2))=3,14159273001...
(79)

(Wells 1986, p. 54) como primera aproximación y proporcionan, respectivamente, unos 6 y 8 decimales por término. Tales series existen debido a la racionalidad de varios invariantes modulares.

La forma general de la serie es

suma_(n=0)^infty((6n)!)/((3n)!(n!)^3)1/(^n)=(sqrt(-j(t)))/pi,
(80)

donde t es un discriminante de la forma cuadrática binaria, j(t) es la función j,

b(t) = sqrt(t)
(81)
a(t) = (b(t))/6{1-(E_4(t))/(E_6(t))},
(82)

y la E_i son series de Eisenstein. Un campo de números de clase p implica enteros algebraicos de grado p de las constantes A=a(t), B=b(t), y C=c(t). De todas las series que constan sólo de términos enteros, la que da más dígitos numéricos en el menor período de tiempo corresponde al mayor discriminante de la clase número 1 de d=-163 y fue formulada por los hermanos Chudnovsky (1987). El 163 que aparece aquí es el mismo que aparece en el hecho de que e^(pisqrt(163)) (la constante de Ramanujan) es casi un número entero. Del mismo modo, el factor 640320^3 proviene de la identidad de la función j para j(1/2(1+isqrt(163))). La serie viene dada por

1/pi = 12suma_(n=0)^(infty)((-1)^n(6n)!(13591409+545140134n))/((n!)^3(3n)!(640320^3)^(n+1/2))
(83)
= (163·8·27·7·11·19·127)/(640320^(3/2))sum_(n=0)^(infty)((13591409)/(163·2·9·7·11·19·127)+n)((6n)!)/((3n)!(n!)^3)((-1)^n)/(640320^(3n))
(84)

(Borwein y Borwein 1993; Beck y Trott; Bailey et al. 2007, p. 44). Esta serie da 14 dígitos exactos por término. La misma ecuación en otra forma fue dada por los hermanos Chudnovsky (1987) y es utilizada por Wolfram Language para calcular pi (Vardi 1991; Wolfram Research),

pi=(426880sqrt(10005))/(A),
(85)

donde

A = 13591409
(86)
B = -1/(151931373056000)
(87)
C = (30285563)/(1651969144908540723200).¡
(88)

La mejor fórmula para la clase número 2 (mayor discriminante -427) es

1/pi=12suma_(n=0)^infty((-1)^n(6n)!(A+Bn))/((n!)^3(3n)!C^(n+1/2)),
(89)

donde

A = 212175710912sqrt(61)+1657145277365
(90)
B = 13773980892672sqrt(61)+107578229802750
(91)
C = ^3
(92)

(Borwein y Borwein 1993). Esta serie añade unos 25 dígitos por cada término adicional. La serie de convergencia más rápida para la clase número 3 corresponde a d=-907 y da 37-38 dígitos por término. La serie de más rápida convergencia de la clase número 4 corresponde a d=-1555 y es

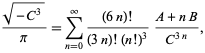(sqrt(-C^3))/pi=sum_(n=0)^infty((6n)!)/((3n)!(n!)^3)(A+nB)/(C^(3n)),
(93)

donde

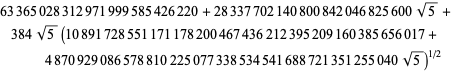A = 63365028312971999585426220+28337702140800842046825600sqrt(5)+384sqrt(5)(10891728551171178200467436212395209160385656017+4870929086578810225077338534541688721351255040sqrt(5))^(1/2)
(94)
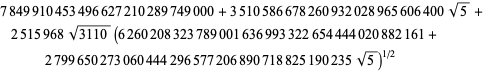B = 7849910453496627210289749000+3510586678260932028965606400sqrt(5)+2515968sqrt(3110)(6260208323789001636993322654444020882161+2799650273060444296577206890718825190235sqrt(5))^(1/2)
(95)
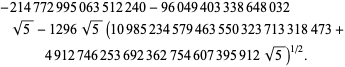C = -214772995063512240-96049403338648032sqrt(5)-1296sqrt(5)(10985234579463550323713318473+4912746253692362754607395912sqrt(5))^(1/2).
(96)

Esto da 50 dígitos por término. Borwein y Borwein (1993) han desarrollado un algoritmo general para generar tales series para un número de clase arbitrario.

Una lista completa de las series de Ramanujan para 1/pi que se encuentran en sus cuadernos segundo y tercero está dada por Berndt (1994, pp. ¡352-354),

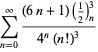4/pi = suma_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!¡)^3)
(97)
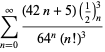(16)/pi = suma_(n=0)^(infty)((42n+5)(1/2)_n^3)/(64^n(n!)^3)
(98)
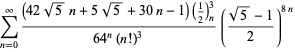(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(99)
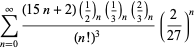(27)/(4pi) = sum_(n=0)^(infty)((15n+2)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(2/(27))^n
(100)
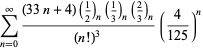(15sqrt(3))/(2pi) = sum_(n=0)^(infty)((33n+4)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(4/(125))^n
(101)
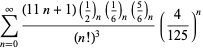(5sqrt(5))/(2pisqrt(3)) = sum_(n=0)^(infty)((11n+1)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(125))^n
(102)
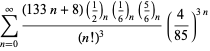(85sqrt(85))/(18pisqrt(3)) = sum_(n=0)^(infty)((133n+8)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(85))^(3n)
(103)
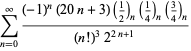4/pi = sum_(n=0)^(infty)((-1)^n(20n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^32^(2n+1))
(104)
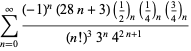4/(pisqrt(3)) = sum_(n=0)^(infty)((-1)^n(28n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^33^n4^(2n+1))
(105)
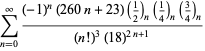4/pi = sum_(n=0)^(infty)((-1)^n(260n+23)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(18)^(2n+1))
(106)
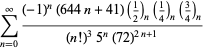4/(pisqrt(5)) = sum_(n=0)^(infty)((-1)^n(644n+41)(1/2)_n(1/4)_n(3/4)_n)/((n!)^35^n(72)^(2n+1))
(107)
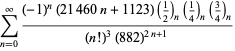4/pi = sum_(n=0)^(infty)((-1)^n(21460n+1123)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(882)^(2n+1))
(108)
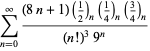(2sqrt(3))/pi = sum_(n=0)^(infty)((8n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^n)
(109)
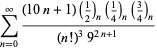1/(2pisqrt(2)) = sum_(n=0)^(infty)((10n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^(2n+1))
(110)
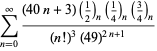1/(3pisqrt(3)) = sum_(n=0)^(infty)((40n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(49)^(2n+1))
(111)
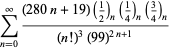2/(pisqrt(11)) = sum_(n=0)^(infty)((280n+19)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(2n+1))
(112)
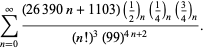1/(2pisqrt(2)) = sum_(n=0)^(infty)((26390n+1103)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(4n+2)).
(113)

Estas ecuaciones fueron demostradas por primera vez por Borwein y Borwein (1987a, pp. 177-187). Borwein y Borwein (1987b, 1988, 1993) demostraron otras ecuaciones de este tipo, y Chudnovsky y Chudnovsky (1987) encontraron ecuaciones similares para otras constantes trascendentales (Bailey et al. 2007, pp. 44-45).¡

Una lista completa de ecuaciones independientes conocidas de este tipo viene dada por

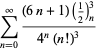4/pi = suma_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!¡)^3)
(114)
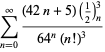(16)/pi = suma_(n=0)^(infty)((42n+5)(1/2)_n^3)/(64^n(n!)^3)
(115)
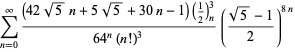(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(116)
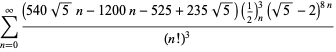(5^(1/4))/pi = suma_(n=0)^(infty)((540sqrt(5)n-1200n-525+235sqrt(5))(1/2)_n^3(sqrt(5)-2)^(8n))/((n!)^3)
(117)
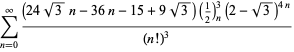(12^(1/4))/pi = suma_(n=0)^(infty)((24sqrt(3)n-36n-15+9sqrt(3))(1/2)_n^3(2-sqrt(3))^(4n))/((n!)^3)
(118)

para m=1 con signos no alternos,

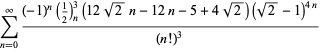2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(12sqrt(2)n-12n-5+4sqrt(2))(sqrt(2)-1)^(4n))/((n!)^3)
(119)
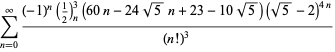2/pi = suma_(n=0)^(infty)((-1)^n(1/2)_n^3(60n-24sqrt(5)n+23-10sqrt(5))(sqrt(5)-2)^(4n))/((n!)^3)
(120)
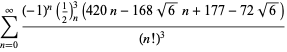2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(420n-168sqrt(6)n+177-72sqrt(6)))/((n!)^3)
(121)
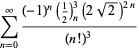(2sqrt(2))/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(2sqrt(2))^(2n))/((n!)^3)
(122)

para m=1 con signos alternos,¡

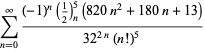(128)/(pi^2) = suma_(n=0)^(infty)((-1)^n(1/2)_n^5(820n^2+180n+13))/(32^(2n)(n!)^5)
(123)
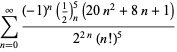(32)/(pi^2) = sum_(n=0)^(infty)((-1)^n(1/2)_n^5(20n^2+8n+1))/(2^(2n)(n!)^5)
(124)

para m=2 (Guillera 2002, 2003, 2006),

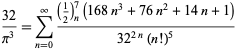(32)/(pi^3)=sum_(n=0)^infty((1/2)_n^7(168n^3+76n^2+14n+1))/(32^(2n)(n!)^5)
(125)

para m=3 (Guillera 2002, 2003, 2006), y no se conocen otros para m3 (Bailey et al. 2007, pp. 45-48).

Bellard da la exótica fórmula

pi=1/(740025),
(126)

where

P(n)=-885673181n^5+3125347237n^4-2942969225n^3+1031962795n^2-196882274n+10996648.
(127)

Gasper cita el resultado

pi=(16)/3^(-1),
(128)

donde _1F_2 es una función hipergeométrica generalizada, y la transforma en

pi=lim_(x-infty)4x_1F_2(1/2;3/2,3/2;-x^2).
(129)

Un resultado fascinante debido a Gosper viene dado por

lim_(n-infty)product_(i=n)^(2n)pi/(2tan^(-1)i)=4^(1/pi)=1,554682275....
(130)

pi satisface la desigualdad

(1+1/pi)^(pi+1) aprox 3,14097pi.
(131)

D. Terr (com. pers.) observó la curiosa identidad

(3,1,4)=(1,5,9)+(2,6,5) (mod 10)
(132)

que implica los 9 primeros dígitos de pi.

Deja una respuesta

Tu dirección de correo electrónico no será publicada.