A váltakozó áramot, azaz a váltakozó áramot azért nevezik így, mert az áram két polaritás között váltakozik vagy váltakozik. Más szóval az áram (és következésképpen a feszültség) az idő függvénye. Ez alapvetően különbözik az egyenáramtól, amelynek polaritása rögzített és általában időben állandó. Egy laboratóriumi egyenáramú feszültségforrás például ideális esetben egy meghatározott feszültséget tart fenn a kapcsain, és nem változik az idő múlásával. Ezzel szemben, ahogy egy váltakozó áramú hullámforma ide-oda leng az időben, alakja széles variációkat mutathat, kezdve a laboratóriumi szabványok egyszerű, szabályos útjaitól, mint például a szinuszhullámok, háromszöghullámok és négyszöghullámok, egészen a hangszerek és az emberi hang által létrehozott sokkal összetettebb és hullámzó hullámformákig.
A szinuszhullám a legegyszerűbb hullám, amely létrehozható. Egy egyszerű, állandó sebességgel forgó vektor mozgását reprezentálja, mint például egy óra másodpercmutatójának függőleges elmozdulása. Egy példa látható a \(\PageIndex{1}\) ábrán. A vízszintes tengely az időt ábrázolja. Balról jobbra haladva növekszik (azaz ha az A pont a B ponttól jobbra van, akkor A később következik be, mint B). A függőleges tengelyt itt általában a maximum százalékában ábrázoljuk, de általában a feszültség, az áram, a hangnyomás vagy hasonló mérőszámok lennének.
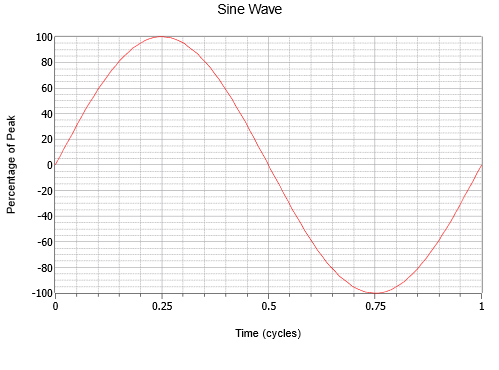
Ábra \(\PageIndex{1}\):
Figyeljük meg a sima változást, amely nulláról indul, negyedére pozitív csúcsra emelkedik, félúton visszaesik nullára, háromnegyedére negatív csúcsra emelkedik, majd ismét emelkedik oda, ahonnan indult. Ez a folyamat ezután megismétlődik. Minden egyes ismétlést ciklusnak nevezünk. A \(\PageIndex{1}\) ábrán egy teljes ciklus látható.
A szinuszhullámok negyedhullámos szimmetriát mutatnak. Ez azt jelenti, hogy a hullám minden egyes negyede (időben) megegyezik bármelyik másikkal, ha egyszerűen megfordítjuk a vízszintes tengely körül és/vagy függőlegesen elforgatjuk a csúcspontja körül. Az egy ciklus teljesítéséhez szükséges időt periódusnak nevezzük, és \(T\) (az Idő) szimbólummal jelöljük. A periódus reciproka a frekvencia, \(f\).
\
A frekvencia azt mutatja, hogy hány ciklus van egy másodpercben. A terület egyik 19. századi kutatójának tiszteletére ahelyett, hogy a mértékegységet másodpercenkénti ciklusnak neveznénk, a Heinrich Hertzről elnevezett Hertz-et használjuk, rövidítve Hz. A \(\PageIndex{2}\) ábrán három szinuszhullám látható különböző frekvenciákkal; a kezdeti hullám (zöld), egy hullám a frekvencia kétszeresével (kék), és egy harmadik a frekvencia felével vagy a periódus kétszeresével (piros).
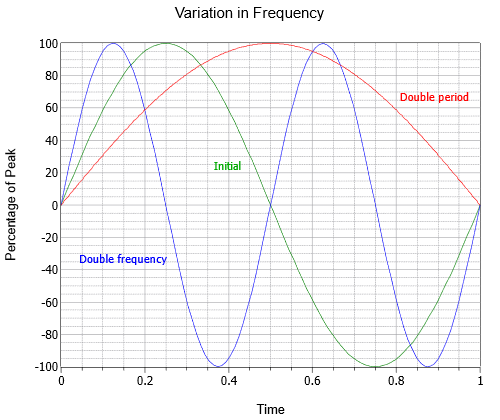
Az \(\PageIndex{2}\) ábra: Szinuszhullám frekvenciaváltozása.
A hullám amplitúdója (függőleges) csúcsmennyiségként fejezhető ki, amely a középső nulla vonaltól a legpozitívabb értékig tartó változás. Az amplitúdó csúcs-csúcs értékként is kifejezhető; a legnegatívabb értéktől a legpozitívabb értékig terjedő távolság. Egy szinuszhullám esetében ez mindig a csúcsérték kétszerese, bár más hullámok esetében, amelyek aszimmetrikusak lehetnek, ez nem biztos, hogy így van. A \(\PageIndex{3}\) ábra három különböző amplitúdójú szinuszhullámot mutat be. A kezdeti (zöld) mellett kétszeres amplitúdójú (kék) és fél amplitúdójú (piros) változatok láthatók.
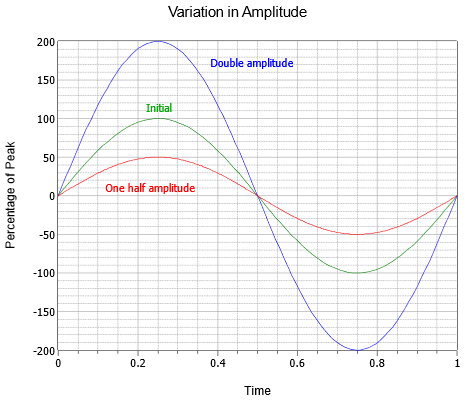
\(\PageIndex{3}\) ábra: Szinuszhullám amplitúdóváltozása.
Ezeket a paramétereket kombinálva tekintsük a \(\PageIndex{4}\) ábrán látható feszültséghullámformát. Itt egy váltakozó feszültségű hullámforma két ciklusát látjuk.
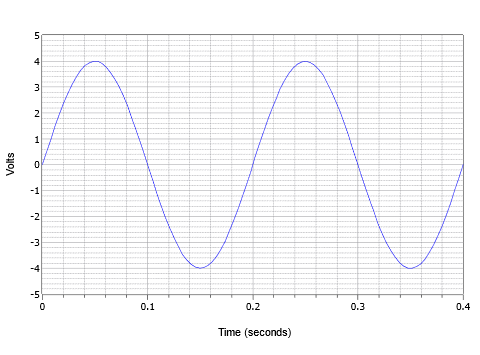
Az \(\PageIndex{4}\) ábra: Alapvető szinuszhullám példa.
A csúcsérték 4 volt, a csúcstól-csúcsig érték pedig 8 volt (jellemzően “8 V pp” rövidítéssel). Egy ciklus időtartama 0,2 másodperc, vagy \(T = 200\) ezredmásodperc. Továbbá a frekvencia \(f = 1/200\) milliszekundum, vagy 5 Hz (5 ciklus egy másodperc alatt).
A váltakozó áramú hullámformák egyenáramú eltolással is kombinálhatók. Egy pozitív DC szint hozzáadása függőlegesen felfelé tolja el a hullámot, míg egy negatív DC szint függőlegesen lefelé tolja el a hullámot. Ez nem változtatja meg az amplitúdó frekvenciáját vagy váltakozó áramú részét (bár az abszolút csúcsok az egyenáramú értékkel eltolódnak). A \(\PageIndex{5}\) ábra a különböző DC-eltolódások hatását mutatja. A kezdeti hullám felett (zöld) egy egyébként azonos hullám látható az eredeti csúcsérték 20%-ának megfelelő pozitív DC-eltolással (kék). Az eredeti alatt egy harmadik hullám (piros) található, amely az eredeti csúcsérték felének megfelelő negatív DC-eltolódást mutat.
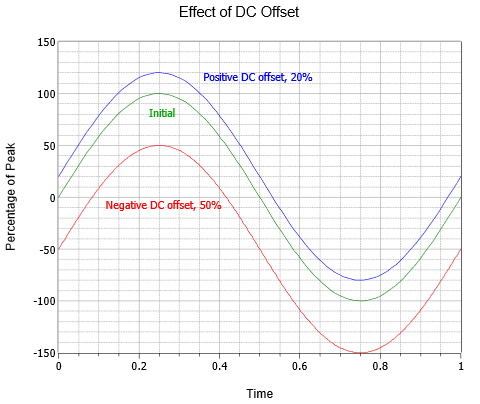
\(\PageIndex{5}\) ábra: Szinuszhullám DC-eltolásának változása.
Ezeken túlmenően lehetséges, hogy egy szinuszhullám időben eltolódik valamilyen más szinuszhullámhoz vagy referenciához képest. Bár ezt az eltolódást abszolút időben is meg lehet adni, gyakoribb, hogy ezt fáziseltolódásként, azaz a periódus egy részeként, fokokban kifejezett időként tesszük. Például, ha az egyik szinusz a periódus negyedével előzi meg a másikat, akkor azt mondjuk, hogy 90\(^{\circ}\) (azaz a 360\(^{\circ}\) 1/4-ével) vezet. Ha a periódus ½-ével van lemaradva, akkor 180\(^{\circ}\) (azaz 1/2 ciklusnyi idővel később). Másképpen fogalmazva: a vezető hullámformák időben korábban kezdődnek, és így a referenciától balra, míg a lemaradó hullámformák időben később kezdődnek, és jobbra rajzolódnak.
Az \(\PageIndex{6}\) ábra a fáziseltolódás hatását szemlélteti. Vegyük észre, hogy ezen az ábrán a \(t = 0\) a vízszintes tengely közepére került. A középső görbe a kezdeti vagy referenciahullám (zöld). Balra (piros) a kezdeti hullámot egy nyolcadik ciklussal megelőző hullám, azaz 45\(^{\circ}\). Jobbra (kék) egy feleannyival lemaradó hullám, vagyis -22,5\(^{\circ}\).
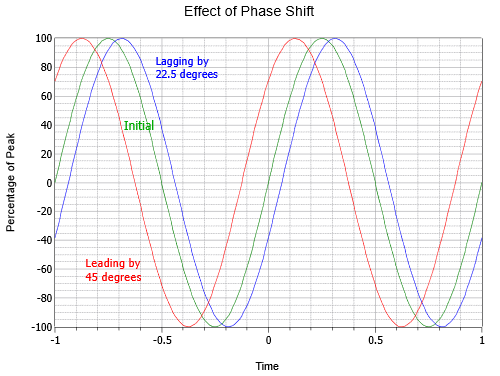
Ábra \(\PageIndex{6}\): Szinuszhullám fázisváltozása.
A fenti elemek kombinálásával kialakíthatjuk a szinuszhullám általános formátumát (a feszültséget ábrázolva):
\
Hol
\(v(t)\) a feszültség valamilyen \(t\) időpontban,
\(V_{DC}\) az egyenáramú eltolás, ha van,
\(V_{P}\) a csúcsérték,
\(f\) a frekvencia,
\(\theta\) a fáziseltolódás (+, ha előretolt és balra húzott, – ha lemaradt és jobbra húzott).
Egy gyors és gyakorlati példával élve, az \(\PageIndex{4}\) ábrán látható hullámforma amplitúdója 4 volt csúcsérték, frekvenciája 5 Hz, és nincs DC eltolás vagy fáziseltolódás. Így a kifejezése \(v(t) = 4 \sin (2 \pi 5 t)\)
A fáziseltolódás kiszámításához először határozzuk meg a hullámforma és a referencia közötti időkülönbséget, amelyet \(\Delta t\)-nek nevezünk. A referencia lehet egy fix időpont (pl. \(t = 0\)) vagy egy másik hullámforma. Általában a legegyszerűbb módja ennek az, hogy megmérjük a különbséget a zérusátmeneteknél, feltételezve, hogy nincs egyenáramú eltolás. Ha van eltolás, végezze el a mérést ott, ahová a zérusátmenet eltolódott (azaz a DC-eltolás szintjén). Ha megvan a különbség, ossza el a periódussal, hogy az eltolódást a periódus törtrészeként ábrázolja. Mivel egy ciklus a vektor egy fordulatát, azaz 360 fokot jelent, egyszerűen szorozza meg a törtet 360 fokkal, hogy megtalálja a fáziseltolódást fokban. Képletben kifejezve:
\
Memlékezzünk arra, hogy ha a hullám balra tolódik, akkor az előremutató és pozitív, míg a jobbra tolódás időben elmaradó vagy késleltetett, tehát negatív.
Példa \(\PageIndex{1}\)
Írd meg az \(\PageIndex{7}\) ábrán látható hullámforma kifejezését.
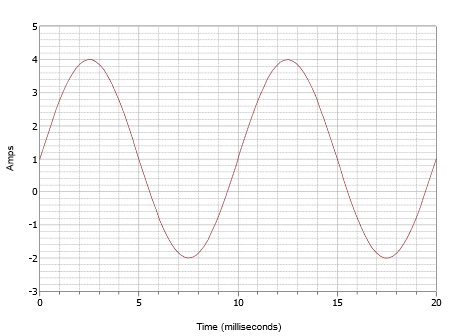
Ábra \(\PageIndex{7}\): \(\PageIndex{1}\).
Ez a hullámforma felületesen úgy néz ki, mint az \(\PageIndex{4}\) ábra, de ne hagyja, hogy ez megtévessze. Először is, az időskála más. Ennél a hullámformánál egy ciklus 10 milliszekundum alatt fejeződik be. Ezért a frekvencia
\
\
\
\
A második probléma az egyenáramú eltolás. Vegyük észre, hogy a pozitív csúcs 4 amperrel, míg a negatív csúcs -2 amperrel jelentkezik. Ez egy 6 amperes csúcs-csúcsértéket jelez. Offszet nélkül a pozitív csúcs 3 amperrel lenne, tehát +1 amper DC offset van. A hullámforma függőleges középpontja 0 amperről +1 amperre tolódik felfelé. Ez a pont t = 0-nál van, ezért nincs fáziseltolódás. A kapott kifejezés:
\
Példa \(\PageIndex{2}\)
Az \(\PageIndex{8}\) ábrán látható hullámforma kifejezésének megírása.
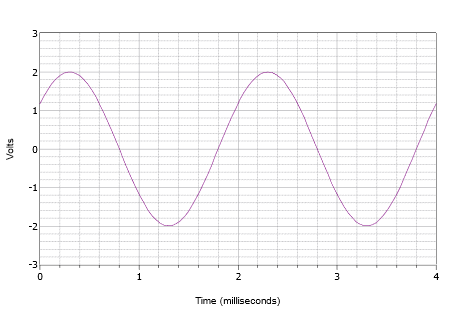
Ábra \(\PageIndex{8}\): \(\PageIndex{2}\).
Először is, a pozitív csúcs 2 volt, és a csúcs-csúcs érték 4 volt. Ezért nincs egyenáramú eltolás. A hullám függőleges középpontja nem a \(t = 0\) pontban kezdődik, ezért fáziseltolódásnak kell lennie. Az \(t = 0\) érték 1,2 volt. A hullám ugyanezt az amplitúdót \(t = 2\) ezredmásodpercnél éri el, és újabb ciklus ismétlésébe kezd. Következésképpen a periódusnak 2 milliszekundumnak kell lennie. A frekvencia ennek az értéknek a reciproka, tehát \(f = 500\) Hz.
A hullámforma balra tolódik, ami pozitív vagy vezető fáziseltolódást jelez. Ha megvizsgáljuk a második ciklust, láthatjuk, hogy 1,8 ezredmásodpercnél éri el a nulla voltot. Ezért az eltolódás 0,2 ezredmásodperc. Fokokban kifejezve ez:
\
\
\
\
A végső kifejezés:
\
Példa \(\PageIndex{3}\)
Rajzolja meg a következő kifejezésnek megfelelő hullámformát.
\
Először is figyeljük meg, hogy a -3 voltos eltolás a pozitív csúcsot 5 voltról 2 voltra, a negatív csúcsot pedig -5 voltról -8 voltra nyomja le. A 40 kHz-es frekvencia a következő periódust diktálja:
\
\
\
A -72\(^{\circ}\) fáziseltolódás 72/360, azaz 0,2 ciklust jelent. Ez 0,2-szer 25 \(\mu\)s, azaz 5 \(\mu\)s (jobbra eltolva, mert negatív) 0,2-szeres időbeli késleltetésnek felel meg.
Az ábrát gyakran a legjobb diszkrét lépések sorozatán keresztül felépíteni, ahelyett, hogy az egészet egyszerre próbálnánk megrajzolni. Először rajzoljunk egy szinuszhullámot 5 voltos csúcsamplitúdóval és 25 \(\(\mu\)s periódussal. Most nyomjuk lefelé a hullámformát 3 voltra, hogy a pozitív csúcs csak 2 voltos legyen, a negatív csúcs pedig -8 voltos. Végül toljuk az újonnan eltolt hullámformát 5 \(\mu\)s-mal jobbra. Az eredmény a \(\PageIndex{9}\) ábrán látható.
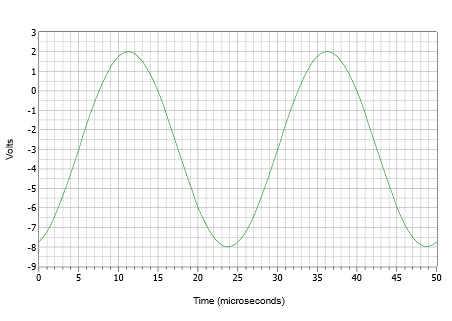
Az \(\PageIndex{9}\) ábra: \(\PageIndex{3}\).
1.2.1: Laboratóriumi mérések
A laboratóriumban egy függvénygenerátort használunk szinuszok és más hullámformák előállítására. Ezek az eszközök lehetővé teszik mind a hullám amplitúdójának, mind a frekvenciájának pontos szabályozását a DC-eltolás hozzáadásával együtt, ha szükséges. Egy példa a \(\PageIndex{10}\) ábrán látható. A megfelelő mérőeszköz az oszcilloszkóp, vagy röviden csak scope.

Ábra \(\PageIndex{10}\): Laboratóriumi jelgenerátor.
Az oszcilloszkóp talán a leghasznosabb és legsokoldalúbb mérőeszköz a laboratóriumban. Általában két vagy négy bemeneti csatornával rendelkeznek, bár ennél több is lehetséges. Minden bemeneti csatorna saját érzékenységbeállítással rendelkezik, és minden csatorna közös időreferencián osztozik. A kijelző a \(\PageIndex{1}\) – \(\PageIndex{9}\) ábrákon látható hullámformákat rajzolja ki. Emellett ábrázolhatnak egy feszültséget egy másik feszültséggel szemben (X – Y mód). A modern oszcilloszkópok további funkciókkal rendelkeznek, mint például a frekvencia, amplitúdó, fáziseltolódás stb. automatikus mérése, kurzor alapú mérések, és a kijelző képének grafikus fájlként való mentése. Egy négycsatornás digitális oszcilloszkóp példája a \(\PageIndex{11}\) ábrán látható.

Az \(\PageIndex{11}\) ábra: Egy digitális oszcilloszkóp.
1.2.2:
Az \(\PageIndex{12}\) ábra a váltakozó áramú feszültség- és áramforrások szimbólumait mutatja. A polaritás- és irányjelzések nem abszolút értékűek; elvégre olyan váltakozó áramú forrásokról van szó, amelyek polaritása és iránya ide-oda változik. A jelölések inkább az időzítési referencia létrehozására szolgálnak, különösen a több forrást alkalmazó áramkörökben.
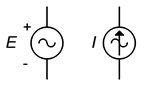
\(\PageIndex{12}\) ábra: Váltakozó áramú feszültségforrás (balra) és áramforrás (jobbra) sematikus szimbólumai.
Azért érdemes megjegyezni, hogy egy forrás negálása ugyanaz, mint a polaritásának megfordítása. Ez igaz volt az egyenáramú forrásokra, és igaz marad a váltakozó áramú forrásokra is. Ezt szemlélteti a \(\PageIndex{13}\) ábra. Néha a forrás megfordítása vagy negálása egy kicsit nyilvánvalóbbá vagy könnyebben szemléltethetővé teszi az elemzést.
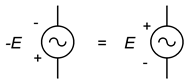
A \(\PageIndex{13}\) ábra: Polaritás/jel egyenértékűség.
Példa \(\PageIndex{4}\)
Tegyük fel, hogy egy oszcilloszkóp két hullámot jelenít meg az \(\PageIndex{14}\) ábrán látható módon. Határozza meg a kisebb, 20 voltos csúcsú (kék) hullámforma fáziseltolódását a nagyobb, 25 voltos csúcsú (piros) hullámformához képest.
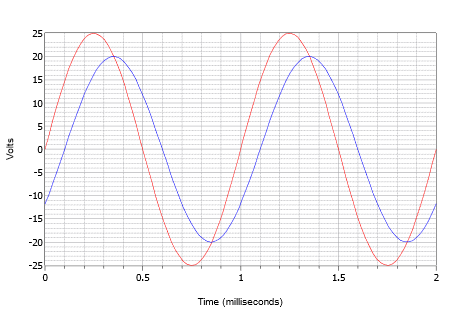
Ábra \(\PageIndex{14}\): A \(\PageIndex{4}\) példa hullámformái.
Először is, vegye figyelembe, hogy egyik hullám sem mutat egyenáramú eltolódást. Ha az egyiknek vagy mindkettőnek lenne eltolódása, akkor a hullám(ok)at függőlegesen el kellene tolni, hogy a normál nullpontjaik azonos szinten legyenek. Mindkét hullámot mérve a periódus 1 ezredmásodpercnek adódik. Az időeltolódás legegyszerűbben a nullpontok bármelyikénél megállapítható (négy hely közül lehet választani). A késés egy kis eltérés, azaz 0,1 ezredmásodperc, a kisebb hullám időben késik, vagy lemarad a nagyobb hullámtól. Ez negatív fáziseltolódást jelez.
\
\
\
\
1.2.3. Fáziseltolódást jelez:
Van egy maroknyi speciális fáziseltolódás, amit érdemes közelebbről megvizsgálni. Ha egy szinuszhullámot invertálunk, azaz fejjel lefelé fordítunk, akkor megkülönböztethetetlen egy +180 vagy -180 fokkal eltolt szinuszhullámtól. Más szóval egy ilyen hullám háromféleképpen írható fel: \(- \sin (2 \pi ft)\), \(\sin (2 \pi ft – 180^{\circ})\), vagy \(\sin (2 \pi ft + 180^{\circ})\). Továbbá, ha egy szinuszhullám +90 fokkal eltolódik (azaz előre és balra), akkor kozinuszhullámnak is nevezhetjük. Így \(\sin (2 \pi ft + 90^{\circ}) = \ cos (2 \pi ft)\). Végül, ha egy szinuszhullám -90 fokkal eltolódik (azaz elmarad és jobbra tolódik), akkor negatív vagy fordított koszinuszhullámnak nevezhetjük. Így \(\sin (2 \pi ft – 90^{\circ}) = – \cos (2 \pi ft)\). E négy hullám összefüggéseit a \(\PageIndex{15}\) ábra szemlélteti.
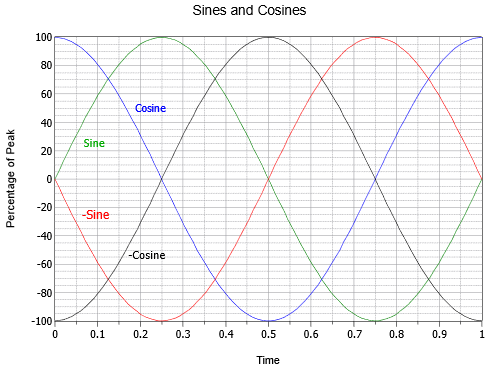
Ábra \(\PageIndex{15}\): A szinuszok és koszinuszok időbeli összefüggései.
Azt is érdemes megjegyezni, hogy a koszinuszhullám a szinuszhullám első deriváltját vagy meredekségét jelenti. Ahogyan más tanulmányokból talán emlékszik, egy egyenes meredeksége vagy “meredeksége” a függőleges változás és a vízszintes változás aránya, amit néha “emelkedésnek neveznek a lefutáshoz képest”. Egy feszültség esetében ez a feszültség változása az időváltozáshoz képest, vagy \(\Delta V/ \Delta t\). Egy sima, folyamatosan változó görbe, például egy szinuszhullám esetében a meredekséget egy adott pontban megfelelően az első deriváltként határozzuk meg, vagy ebben az esetben \(dv/dt\). Hogy vizuálisan meggyőződjünk arról, hogy ez igaz, figyeljük meg, hogy a szinuszhullám legmeredekebb része (zöld) ott van, ahol a hullám amplitúdója nulla. Amint pozitív irányban halad át a nullán (\(t = 0\) vagy \(t = 1\) az \(\(\PageIndex{15}\) ábrán), a koszinusz (kék) a pozitív csúcsán van. Mivel a szinusz negatív irányban halad át a nullán (\(t = 0,5\)), a koszinusz negatív csúcsán van. Továbbá a szinuszhullám a pozitív és negatív csúcspontjainál (\(t = 0,25\) és \(t = 0,75\) pontoknál) nulla meredekségű, és ekkor a koszinusz amplitúdója is nulla. Az is igaz, hogy a szinuszhullám a negatív koszinuszhullám meredeksége, a negatív koszinusz a negatív szinusz meredeksége, a negatív szinusz pedig a koszinusz meredeksége. Fordított irányban haladva azt mondhatjuk, hogy a koszinuszhullám ellenszármazéka (határozatlan integrálja) a szinuszhullám, a szinuszhullám integrálja a negatív koszinuszhullám, és így tovább. Ezek az összefüggések akkor bizonyulnak majd a leghasznosabbnak, amikor a váltakozó áramú áramkörökben a kondenzátorok és induktivitások válaszára fordítjuk figyelmünket.
1.2.4: RMS – Root Mean Square Measurement
A csúcsérték és a csúcsérték-csúcsérték mellett az amplitúdó is megadható RMS (Root Mean Square) értékként. Valójában, ha a csúcs vagy a csúcs-csúcs-csúcs érték nincs megadva, a mérést RMS értéknek kell feltételezni. Az RMS egy speciális számítás, amelyet egyenértékű egyenáramú teljesítmény meghatározására használnak (nagyon gyakori például hangerősítőknél). Más szóval, ha egy ellenállásban lévő teljesítmény meghatározására vagyunk kíváncsiak, a számítást a feszültség vagy az áram RMS értékeivel kell elvégezni, nem pedig a csúcs- vagy csúcs-csúcsértékekkel. Ennek elmulasztása hibás teljesítményeket eredményez. Ez a hullámformától függetlenül igaz; legyen az szinuszhullám, háromszöghullám vagy a zenei jelek komplex hullámai. Ha egy feszültséget effektív értékként adunk meg, akkor az a teljesítményszámításokhoz ugyanúgy kezelhető, mint egy hasonló méretű egyenfeszültség. Például egy 1 voltos RMS szinusz ugyanolyan teljesítményleadást és felmelegedést eredményez egy adott ellenállásban, mint 1 voltos egyenfeszültség. Emiatt az RMS-t néha effektív értéknek (azaz effektív egyenáramú értéknek) nevezik.
A négyzetes középérték elnevezés az effektív érték meghatározásának folyamatát írja le. Először is emlékezzünk arra, hogy a teljesítmény arányos a feszültség vagy az áram négyzetével. Így első lépésünk a bemeneti hullámforma négyzetre állítása lesz. Természetesen a hullámforma az idő függvénye, és a négyzete valamilyen új alakot fog eredményezni. Ezen a ponton meg kell találnunk ennek az új alaknak az átlagértékét. Ennek oka egyszerű, de nem feltétlenül nyilvánvaló. Az elektromos és elektronikus alkatrészek tömeggel rendelkeznek, és így nem melegszenek vagy hűlnek le azonnal. Termikus időállandóval rendelkeznek. Ezért az idő múlásával az átlagos bemeneti értékre reagálnak. Bár kiszámíthatnánk valamilyen módon a “pillanatnyi csúcsteljesítményt” egy adott időpillanatban, ez nem jelenti az egyenáramú egyenáramú teljesítményt. Miután megkaptuk ennek a négyzetes hullámformának az átlagértékét, a megfelelő egyenáramú érték csak az átlag négyzetgyöke. Az eredmény egy nulla és egy közötti tört érték, amelyet skálázási tényezőként használunk, hogy a csúcsértéket RMS-értékké alakítsuk. Az érték egyedi lesz az adott hullámformához. Vagyis minden szinusz (fázistól függetlenül) ugyanolyan tényezővel rendelkezik, minden szabályos háromszöghullám ugyanolyan tényezővel rendelkezik, és így tovább. Mivel leginkább a szinuszokkal foglalkozunk, nézzük meg közelebbről a szinuszok RMS-tényezőjének meghatározását.
Egy egyenáramú eltolás és fáziseltolódás nélküli, egy amplitúdójú szinuszhullám alapkifejezésével kezdjük:
\
Az első lépés ennek a hullámformának a négyzetre állítása. Egy hasznos trigonometrikus azonosság a
\
Ezt a hullámunkra alkalmazva megkapjuk:
\
Ez a kifejezés egy invertált koszinuszhullámot ír le az eredeti frekvencia kétszeresével és az eredeti amplitúdó felével, a csúcsértékével megegyező egyenáramú eltoláson lovagolva. Más szóval a koszinusz negatív csúcsa nulla, a pozitív csúcsa pedig 1. A következő lépés ennek a köztes eredménynek az átlag- vagy középértékének a megtalálása. Az átlag egyenlő a 0,5-es eltolással. Ez úgy ábrázolható, mint az eltolás feletti terület, amely tökéletesen kitölti az eltolás alatti “mélyedést”. Az utolsó lépés az átlag négyzetgyökének kiszámítása. A 0,5 négyzetgyöke egyenlő a kettő négyzetgyökének eggyel többel, azaz körülbelül 0,707-gyel. Ezért az RMS-érték a csúcsérték 0,707-szerese. Alternatív megoldásként a csúcsértéket eloszthatjuk a kettő négyzetgyökével, ami körülbelül 1,414. Ez a folyamat grafikusan a \(\PageIndex{16}\) ábrán látható.
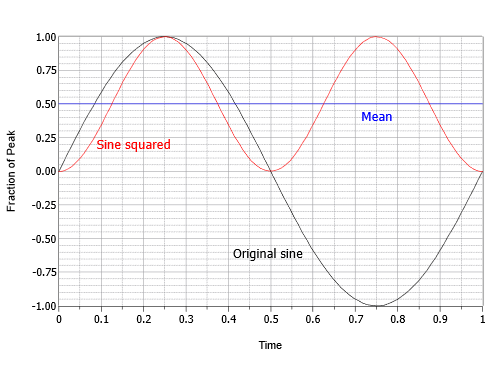
Ábra \(\PageIndex{16}\):
A szinuszhullámok esetében az RMS tényező megtalálásának folyamata.
A szinuszhullámok esetében az RMS mindig a csúcsérték szorozva 0,707-gyel. Azt is mondhatjuk, hogy bármely szinuszhullám RMS értéke a csúcsérték osztva körülbelül 1,414-gyel. Ismétlem, ezek az arányok nem feltétlenül lennének igazak a nem szinuszos hullámokra. Az egyéb gyakori alakzatokra vonatkozó részletek a C. függelékben találhatók. Végül, a csúcsérték és az effektív érték arányát csúcsaránynak nevezzük. Ez a szinuszos hullámok esetében rögzített érték (ismét körülbelül 1,414), de bizonyos típusú hangjelek esetében 10:1-nél nagyobb is lehet.
1.2.5: Hullámhossz
Egy másik érdekes elem a hullám terjedési sebessége. Ez nagymértékben változik. A fény esetében vákuumban (vagy közelítőleg egy elektromos áram esetében egy vezetékben) a sebesség körülbelül 3E8 méter másodpercenként (azaz 300 000 km/s) vagy körülbelül 186 000 mérföld másodpercenként.
A sebesség és az időtartam ismeretében el tudjuk képzelni, hogy a hullám csúcsai milyen távolságra vannak egymástól. Ezt a távolságot nevezzük hullámhossznak, és a görög lambda \(\lambda\) betűvel jelöljük. A hullámhossz egyenlő a sebesség osztva a frekvenciával, \(\lambda = v/f\). Így egy 100 Hz-es szinuszt kibocsátó hangszóró esetében, mivel a hangsebesség a levegőben 344 m/s, akkor \(\lambda = 344 m/s \, / \, 100\) Hz, vagy 3,44 méter (valamivel több mint 11 láb). Vegyük észre, hogy minél nagyobb a frekvencia, annál rövidebb a hullámhossz. Figyeljük meg azt is, hogy minél nagyobb a sebesség, annál hosszabb a hullámhossz. A hullámhossz-számítások különösen fontosak a távközlés és az akusztika területén.