Hogyan gondolkodjunk exponensekkel és logaritmusokkal

Itt egy trükk az exponensekkel és logaritmusokkal kapcsolatos problémák átgondolásához. Csak tegyünk fel két kérdést:

1) Bemenetekről (a változás oka) vagy kimenetekről (a ténylegesen bekövetkezett változás?)

A logaritmusok feltárják a növekedést okozó bemeneteket
Az exponensek megtalálják a növekedés végeredményét

2) A termesztő vagy egy megfigyelő szemszögéből beszélünk?

e és a természetes logaritmus a termesztő pillanatnyi szemszögéből
Bázis 10, bázis 2, stb. az emberi megfigyelő számára kényelmes mérések

A fejemben egy táblázatba rakom a lehetőségeket:

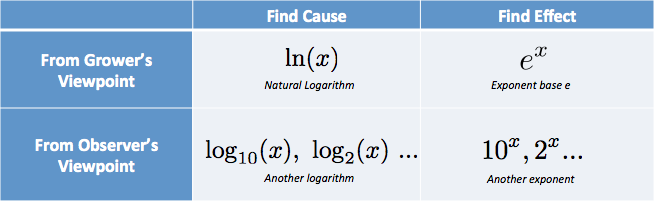
exponens logaritmus szemszögből történő összehasonlítás

olyan gondolataim vannak, hogy “kell az ok, a termesztő szemszögéből nézve… ez a természetes log.”. (A természetes logaritmust kisbetűvel LN-nel rövidítjük, a high-falutin’ logarithmus naturalisból.)

Frusztráltak azok az órák, amelyek a táblázat belső részét, a nyers függvényeket ismertették, anélkül, hogy a feliratok elmagyarázták volna, mikor kell használni őket!

Ez nem fog menni, legyen közvetlen gyakorlat a logaritmusokkal és exponensekkel való gondolkodásban.

Szcenárió: A GDP növekedésének leírása

Itt egy tipikus példa a növekedésre:

2000 és 2010 között az USA GDP-je 9,9 billióról 14,4 billióra változott

Oké, persze, ezek a számok azt mutatják, hogy történt változás. De valószínűleg szeretnénk betekintést nyerni az okokba:

Az agyam rögtön a “logaritmusokra” gondol, mert a növekedéstől visszafelé haladunk az azt okozó arányig. Egy ilyen gondolattal kezdem:

$\displaystyle{\text{változás logaritmusa} \rightarrow \text{a növekedés oka} }$

Egy jó kezdet, de élesítsük ki.

Először is, melyik logaritmust használjuk?

Előre a természetes logaritmust választom. A legtöbb esemény végül is a növekedő (nem a megfigyelő) szempontjából történik, és én szeretek a növekvő elemmel “együtt lovagolni”, hogy szemléltessem, mi történik. (A radiánok hasonlóak: a szögeket a mozgató szempontjából mérik.)

Következő kérdés: milyen változásra alkalmazzuk a logaritmust?

Minket valójában csak a kezdet és a vég közötti arány érdekel: 9,9 billióról 14,4 billióra 10 év alatt. Ez ugyanaz a növekedési ütem, mintha ugyanebben az időszakban \$9,90-ről \$14,40-re mennénk.

A gondolatunkat élesíthetjük:

$\displaystyle{\text{natural logarithm of growth ratio} \rightarrow \text{a növekedés oka} }$

$\displaystyle{\ln(\frac{14.4}{9.9}) = .374}$

Oké, az ok 0,374 vagy 37,4%-os arány volt. Végeztünk?

Még nem. A logaritmusok nem tudnak arról, hogy mennyi ideig tartott egy változás (nem 10 évet dugtunk be, ugye?). Úgy adnak meg egy arányt, mintha az összes változás egyetlen időszakban történt volna.

A változás valóban lehet egyetlen év 37,4%-os folyamatos növekedés, vagy 2 év 18,7%-os növekedés, vagy valamilyen más kombináció.

A forgatókönyvből tudjuk, hogy a változás 10 évig tartott, tehát az aránynak a következőnek kellett lennie:

$\displaystyle{ \text{rate} = \frac{.374}{10} = .0374 = 3.74\%}$

A pillanatnyi, folyamatos növekedés szempontjából az amerikai gazdaság évente 3.74%-kal nőtt.

Végeztünk? Nem egészen!

Ez a folyamatos ütem a növekedés szemszögéből nézve, mintha “együtt lovagolnánk” a gazdasággal, ahogy az változik. Egy bankárt valószínűleg az emberbarát, évenkénti különbség érdekel. Ezt úgy tudjuk kitalálni, hogy a folyamatos növekedést egy évig hagyjuk futni:

$\displaystyle{\text{exponens az árfolyammal és az idővel} \rightarrow \text{a növekedés hatása} }$

$\displaystyle{e^{\text{rate} \cdot \text{idő}} = \text{növekedés}}$

$\displaystyle{e^{.0374 \cdot 1} = 1.0381}$

Az évenkénti növekedés 3,8%, ami valamivel magasabb, mint a 3,74%-os pillanatnyi arány a kamatos kamatozás miatt. Íme egy másik megfogalmazás:

A gazdaság egy adott része pillanatnyi alapon 3,74%-kal növekszik, amit a $e^( modellel modellezünk.0374 * év)$
Egy évenkénti alapon, a halmozódó hatásokat kiszámítva, a gazdaság 3,81%-kal nő, amit $1,0381^év$

A pénzügyekben az évenkénti változásra lehet szükségünk, amit szépen össze lehet hasonlítani más trendekkel. A tudományban és a mérnöki tudományokban inkább pillanatnyi alapon modellezzük a viselkedést.

Scenárió: A természetes növekedés leírása

Utálom az olyan mesterkélt példákat, mint “Tegyük fel, hogy a baktérium 24 óránként megduplázódik, találjuk meg a növekedési képletét.”. Vajon a baktériumtelepek tiszta emberi időközönként szaporodnak, és várunk a pontos megduplázódásra?”

Jobb forgatókönyv: “Hé, találtam néhány baktériumot, vártam egy órát, és a csomó 2,3 grammról 2,32 grammra nőtt. Most megyek ebédelni. Számold ki, mennyi lesz, amikor 3 óra múlva visszajövök.”

Modellezzük le ezt. Szükségünk lesz egy logaritmusra, hogy megtaláljuk a növekedési ütemet, majd egy exponensre, hogy ezt a növekedést előrevetítsük. Mint korábban is, kezdetben tartsunk mindent a természetes logaritmusban.

A növekedési tényező:

$\displaystyle{\text{változás logaritmusa} \rightarrow \text{növekedés oka} }$

$\displaystyle{\ln(\text{növekedés}) = \ln(2.32/2.3) = .0086 = .86\%}$

Ez az arány egy órára, és az általános modell az előrevetítéshez a következő lesz

$\displaystyle{\text{exponens az aránnyal és az idővel} \rightarrow \text{növekedés hatása} }$

$\displaystyle{e^{.0086 \cdot \text{óra}} \rightarrow \text{növekedés hatása} }$

Ha 2,32-ről indulunk és 3 órán át növekszünk, akkor:

$\displaystyle{2,32 \cdot e^{.0086 \cdot 3} = 2,38}$

Csak a vicc kedvéért, mennyi idő alatt duplázódik meg a baktérium? Képzeljük el, hogy megvárjuk, amíg 1-ből 2 lesz:

$\displaystyle{1 \cdot e^{.0086 \cdot \text{hours}} = 2}$

Mechanikusan vehetjük mindkét oldal természetes logaritmusát, hogy “visszavegyük az exponenciát”, de gondolkodjunk inkább intuitívan.

Ha 2 a végeredmény, akkor ln(2) az a növekedési bemenet, ami odavezetett minket (valamilyen sebesség × idő). Tudjuk, hogy a ráta 0,0086 volt, tehát a 2-re jutás ideje:

$\displaystyle{ \text{hours} = \frac{\ln(2)}{\text{rate}} = \frac{.693}{.0086} = 80.58}$

A telep ~80 óra után megduplázódik. (Örülsz, hogy nem maradtál itt?)

Mit jelent valójában a perspektívaváltás?

Megállapítani, hogy a bemenetet (a növekedés oka) vagy a kimenetet (a növekedés eredménye) akarjuk-e, elég egyszerű. De hogyan képzeljük el a növekedési perspektívát?

Tegyük fel, hogy vannak kis munkásaink, akik a végső növekedési mintát építik (lásd az exponensekről szóló cikket):

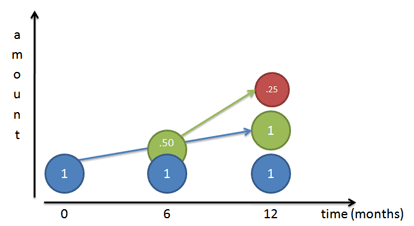
$kamatos kamat$

Ha a növekedési ütemünk 100%, akkor azt mondjuk a kezdeti munkásunknak (Mr. Blue), hogy dolgozzon folyamatosan, és az év végére hozzon létre egy 100%-os másolatot önmagából. Ha napról napra követjük őt, azt látjuk, hogy az év végére valóban elkészíti önmaga 100%-os másolatát (Zöld úr).

De… az a munkás, akit épített (Zöld úr), szintén elkezd dolgozni. Ha Zöld úr először a 6 hónapnál jelenik meg, akkor fél év áll rendelkezésére, hogy dolgozzon (ugyanolyan éves ütemben, mint Kék úr), és megépíti Piros urat. Természetesen Piros úr végül félig kész lesz, mivel Zöld úrnak csak 6 hónapja van.

Mi lenne, ha Zöld úr 4 hónap után jelenne meg? Egy hónap után? Egy nap? Egy másodperc? Ha a munkások azonnal növekedésbe kezdenek, akkor a $e^x$ által meghatározott pillanatról pillanatra görbét kapjuk:

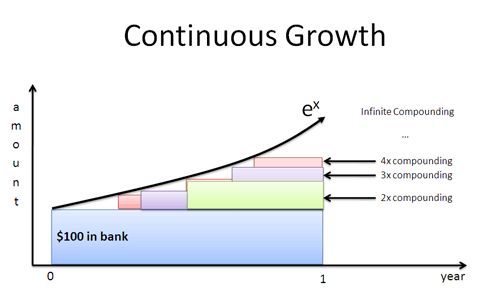
folytonos növekedés

A természetes log adja meg a növekedési ütemet az egyes munkások szemszögéből. Ezt a rátát bedugjuk az $e^x$-be, hogy megtaláljuk a végeredményt, az összes vegyértékkel együtt.

Más bázisok használata

A más típusú logaritmusra váltás (10-es bázis, 2-es bázis stb.) azt jelenti, hogy az általános növekedésben keresünk valamilyen mintázatot, nem pedig azt, hogy az egyéni dolgozó mit csinál.

Minden logaritmus feltesz egy kérdést, amikor változást lát:

Log bázis e: Mekkora volt a pillanatnyi ütem, amit az egyes munkások követtek?
Logbázis 2: Hányszorosára volt szükség?
Logbázis 10: Hányszorosára volt szükség?

Itt egy elemzendő forgatókönyv:

30 év alatt a tranzisztorok száma a tipikus chipeken 1000-ről 1 milliárdra nőtt

Hogyan elemeznéd ezt?

A mikrochipek nem egyetlen egységet alkotnak, amelyek egyenletesen nőnek az idővel. Ezek különálló kiadások, konkurens cégektől, és egy általános technológiai trendet jeleznek.
Mivel nem “lovagolunk” együtt egy bővülő mikrochippel, használjunk egy emberi kényelemre készített skálát. A duplázásra könnyebb gondolni, mint a 10-szeresére.

Ezekkel a feltételezésekkel azt kapjuk:

$\displaystyle{\text{változás logaritmusa} \rightarrow \text{növekedés oka} }$

$\displaystyle{\log_2(\frac{\text{1 milliárd}}{1000}) = \log_2(\text{1 millió}) \sim \text{20 duplázódás}}$

A “növekedés oka” 20 duplázás volt, amelyről tudjuk, hogy 30 év alatt történt. Ez átlagosan 2/3 megduplázódás évente, vagy 1,5 év duplázódásonként – ez egy szép ökölszabály.

A termesztő szemszögéből számolnánk $\ln(\text{1 milliárd}/1000) / \text{30 év} = 46\%$ folyamatos növekedés (ebben a forgatókönyvben kicsit nehezebb viszonyulni).

Elemzésünket táblázatban foglalhatjuk össze:

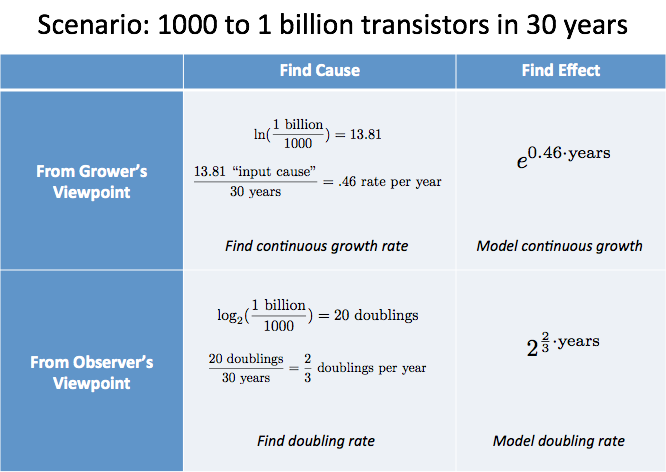
exponens tranzisztor példa

Összefoglalás

A tanulás arról szól, hogy megtaláljuk a fogalom mögötti rejtett feliratokat. Mikor használják? Milyen nézőpontot hoz a problémához?

A jelenlegi értelmezésem szerint az exponensek az ok vs. okozat és a termelő vs. megfigyelő viszonyára kérdeznek rá. De sosem végeztünk; a szórakozás része, hogy megnézzük, hogyan tudjuk újrafogalmazni a régi fogalmakat.

Boldog matematikát.

Függelék: A bázisváltási képlet

Íme, hogyan gondolkodjunk a bázisváltásról. Feltételezve 100%-os folyamatos növekedési ütemet,

ln(x) az az idő, amíg x-re nő
ln(2) az az idő, amíg 2-re nő

Mivel megvan a duplázódás ideje, megnézhetjük, mennyi “férne bele” a teljes időbe, amíg x-re nő:

$\displaystyle{\text{duplázódások száma 1-től x-ig} = \frac{\ln(x)}{\ln(2)} = \log_2(x)}$

Például hány duplázás történik 1-től 64-ig?

Nos, ln(64) = 4,158. És ln(2) = .693. A megfelelő duplázódások száma:

$\displaystyle{\frac{\ln(64)}{\ln(2)} = \frac{4.158}{.693} = 6}$

A való világban a számológépek elveszíthetik pontosságukat, ezért lehetőleg használjunk közvetlen log 2-es bázisú függvényt. És persze lehet tört számunk is: Az 1-től a 2 négyzetgyökéig való eljutás “fél” duplázás, vagy log2(1,414) = 0,5.

A log 10-es bázisra való áttérés azt jelenti, hogy a 10x-ek számát számoljuk, ami belefér:

$\displaystyle{\text{10x-ek száma 1-től x-ig} = \frac{\ln(x)}{\ln(10)} = \log_{10}(x) }$

Jó, nem? További példákért olvassa el a Logaritmusok használata a való világban című részt.

Más hozzászólások ebben a sorozatban

Intuitív útmutató az exponenciális függvényekhez & e
A természetes logaritmus (ln)
A Visual Guide to Simple, Compound and Continuous Interest Rates
Common Definitions of e (Colorized)
Understanding Exponents (Why does 0^0 = 1?)
A logaritmusok használata a való világban
How To Think With Exponents and Logarithms
Understanding Discrete vs. Continuous Growth
What does an exponent really mean?
Q: Why is e special? (2,718…, nem 2, 3,7 vagy más szám?)