Bevezetés
A koordinátatranszformációk 2D-ben nem elég intuitívak, 3D-ben pedig kifejezetten fájdalmasak. Ez az oldal a következő sorrendben foglalkozik velük: (i) vektorok 2-D-ben, (ii) tenzorok 2-D-ben, (iii) vektorok 3-D-ben, (iv) tenzorok 3-D-ben, és végül(v) 4. rangú tenzor transzformációk.
A koordinátatranszformációk egyik fő szempontja a transzformációs mátrix kiértékelése,különösen 3-D-ben. Ezt itt érintjük, és a következő oldalon hosszasan tárgyaljuk.
Nagyon fontos felismerni, hogy ezen az oldalon minden koordinátatranszformáció a koordinátarendszer elforgatása, miközben maga a tárgy fix marad. Az “objektum” lehet egy vektor, például erő vagy sebesség, vagy egy tenzor, például feszültség vagy alakváltozás egy komponensben. A tárgyak elforgatását a későbbi fejezetekben tárgyaljuk.
Vektorok 2D koordináta-transzformációi
A tudományos burgonya kiváló példát nyújt arra, hogyan alkalmazhatók a koordináta-transzformációk a vektorokra, ugyanakkor hangsúlyozza, hogy a koordinátarendszer forog, és nem a vektor… vagy a burgonya.
A bal oldali burgonyán egy vektor van. De koordinátarendszer nélkül nem lehet leírni a vektort.Ezért a jobb oldalon látható módon egy koordinátarendszert adtunk a krumplihoz, így a vektor most már \({\bf v} = 2{\bf i} + 9{\bf j}\).

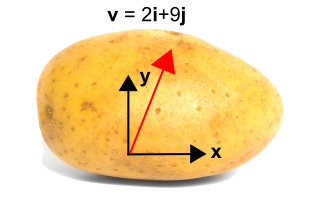
Az alábbiakban kékkel ábrázolt elforgatott koordinátarendszert vezetjük be, használva\(x’\) és \(y’\). Az új rendszert az óramutató járásával ellentétes irányban elforgatjuk az eredeti koordinátarendszerhez képest egy \(\theta\) szöggel. Vegyük észre, hogy maga a vektor egyáltalán nem változik. Ez még mindig ugyanaz a vektor, mint korábban. De az új koordinátarendszerben más számértékekkel íródik le. Ebben az esetben a vektor jobban párhuzamos az új \(x’\) tengellyel, mint az \(y’\) tengellyel, így az \({\bf i’}\) komponens nagyobb lesz, mint az \({\bf j’}\) komponens. A transzformáció az ábra alatt található.
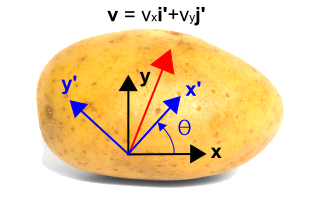
\\\
Azt láthatjuk, hogyEz a négy tényező alkotja a transzformációs egyenletek négy tagját. Ezek könnyen ellenőrizhetők, ha \(\theta = 0^\circ \) és \(\theta = 90^\circ \). Ha \(\theta = 0^\circ\), akkor \(v’_x = v_x\) és \(v’_y = v_y\). Ha \(\theta = 90^\circ\), akkor \(v’_x = v_y\) és \(v’_y = -v_x\).
Transzformációs mátrix
Kényelmesebb a transzformációs egyenleteket mátrixok segítségével leírni (és dolgozni velük).
\\\left\{ \matrix {v_x \\\ v_y} \right\\}}\]
Az \(\cos \theta\) feltételek a mátrix átlóján vannak, míg az \(\sin \theta\)feltételek a mátrix diagonálisán kívül. Az egyetlen lehetséges bökkenő az, hogy ne felejtsük el, melyik \(\sin \theta\) kifejezésen van a mínusz jel. Ez mindig a bal alsó terminus.
A fenti egyenletet mátrixírással úgy írjuk fel, hogy
\
ahol \({\bf Q}\) a transzformációs mátrix szokásos betűje.

Transzformációs vs. rotációs mátrixok
Ha ez a téma még nem lenne elég nehéz, sok könyv és weboldal még tovább növeli a zavart azzal, hogy nem tisztázza, mi a fix és mi a rotációs. Ezen és a következő oldalon a koordinátarendszer az, ami forog, míg a tárgy fix marad.Ezért itt a transzformációs mátrix kifejezést használjuk, hogy ezt hangsúlyozzuk.
A későbbiekben azonban olyan helyzetekkel fogunk foglalkozni, amikor a tárgy forog, míg a koordinátarendszer fix marad. Ebben a forgatókönyvben a rotációs mátrix kifejezést fogjuk használni, hogy hangsúlyozzuk, hogy az objektum forog.
Sok zavar keletkezik abból a meglepő tényből, hogy mindegyik mátrix (transzformáció és forgatás) csak a másik transzponálása! Tehát rendkívül hasonlóan néznek ki. Kétdimenziós problémáknál az egyetlen gyakorlati különbség az, hogy az \(\sin \theta\) előtt lévő mínuszjel az \(q_{12}\) vagy az \(q_{21}\) kifejezésen van-e.
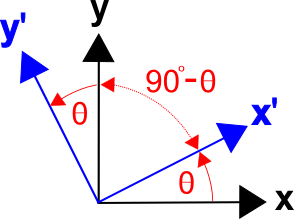
Létezik egy általános módszer a transzformációs mátrixok megfogalmazására, amely a két koordinátarendszer tengelyei közötti szögek koszinuszain, azaz az iránykoszinuszokon alapul. (Ez vonatkozik a háromdimenziós transzformációkra is.) A transzformációs mátrix a következőképpen írható fel:
\\\]
ahol \((x’,x)\) az \(x’\) és \(x\) tengelyek közötti szöget jelenti,\((x’,y)\) az \(x’\) és \(y\) tengelyek közötti szöget stb.
Az \(x’\) és \(y\) közötti szög \((90^\circ – \theta)\), és \(\cos(x’,y) = \cos(90^\circ – \theta) = \sin \theta\).
Hasonlóképpen, az \(y’\) és \(x\) közötti szög \((90^\circ + \theta)\), és \(\cos(y’,x) = \cos(90^\circ + \theta) = -\sin \theta\).
Tenzorjelölés
A koordinátatranszformációt tenzorjelöléssel írjuk fel:
\
ahol \(\lambda_{ij}\) a transzformációs mátrix \({\bf Q}\). (Nem tudom, miért \({\bf Q}\) a mátrixjelölésben, de a tenzorjelölésben \(\lambda_{ij}\), nem pedig \(q_{ij}\)). Az \(\lambda_{ij}\) definíciója a következő:
\
Ha például \(i = 1\) és \(j = 2\), akkor
\
\(\lambda_{ij}\) az \(x’_i\) tengely és az \(x_j\) tengely közötti szög koszinuszának iránya. Ismétlem, ez ugyanúgy alkalmazható a 3D transzformációkra is.
Tenzorok 2D koordinátatranszformációi
Ez a szakasz a tenzortranszformációk mit és hogyanját mutatja be.A miértre későbbre kell várnunk.
A 2. rangú tenzorok koordinátatranszformációi ugyanazt az \({\bf Q}\)mátrixot használják, mint a vektortranszformációk. A feszültségtenzor \(\boldsymbol{\sigma}\) transzformációja a referencia \(x-y\) koordinátarendszerből \(\boldsymbol{\sigma’}\) egy új \(x’-y’\) rendszerben a következőképpen történik.
\
A mátrixok explicit kiírása adja
\ = \left \left \left \left \left \]
(Megjegyezzük, hogy a feszültségtenzor mindig szimmetrikus, még transzformációk után is.)
A mátrixok összeszorzásával megkapjuk
\
Ez a három egyenlet pontosan a feszültségtenzor kétdimenziós transzformációja, amely egy differenciális elemre ható erők összegzéséből és az egyensúlyi állapot megadásából adódik. Ezt a Mohr-kör is ábrázolja.
Tenzorjelölés
A koordinátatranszformációt tenzorjelöléssel írjuk fel:
\
A tenzorjelölés szokás szerint további betekintést nyújt a folyamatba. Ezúttal a betekintést a lambdák indexei adják. Minden lambda gyakorlatilag párosítja az \(\boldsymbol{\sigma’}\) és az \(\boldsymbol{\sigma}\) egy-egy indexét.Ez a tenzor rangjától függetlenül igaz.
Vektorok háromdimenziós koordináta-transzformációi
A kétdimenziós transzformációkban használt általános egyenletek közül sok alkalmazható háromdimenzióban is.Példák:
\\
Csak most a részletek különböznek. A vektorok z-komponensűek, és a transzformációs mátrixok 2×2 helyett 3×3-asak.
\\\]
\\\]
\\ \left\{ \matrix { v_x \\\\ v_y \\\ v_z } \right\}\}\]
Tenzorok háromdimenziós koordináta-transzformációi
Még egyszer, a szabályok nem változnak, csak a részletek.
\
A mátrixok explicit kiírása adja
\ = \left\left\left\left\left\]
Ez a weboldal a háromdimenziós tenzorok koordináta-transzformációit végzi. Próbálja ki.
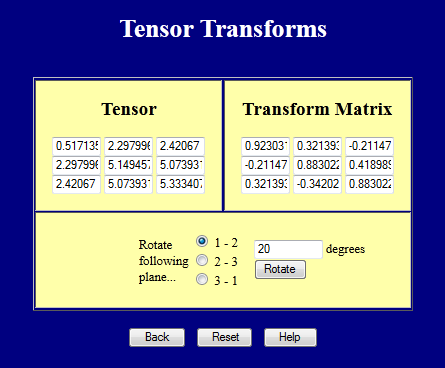
4. rangú tenzorok koordinátatranszformációi
A Hooke-törvényről szóló részben látni fogjuk, hogy a merevségi tenzor 4. rangú, azaz 3x3x3x3 (nem 4×4). Azért írjuk \(C_{ijkl}\), mert minden alakváltozási komponenst, \(\epsilon_{kl}\), bármely feszültségkomponenshez, \(\sigma_{ij}\), viszonyít, azaz, \(\sigma_{ij} = C_{ijkl} \epsilon_{kl}\).A 4. rangú merevségtenzor koordinátatranszformációs törvénye könnyen felírható tenzorjelöléssel a következőképpen
\
A tenzoregyenlet megadja, hogyan kell a transzformációt mátrixjelöléssel felírni.
\
Összefoglaló
Egy vektor koordinátatranszformációja mátrix és tenzor jelölésben
\
Egy tenzor koordinátatranszformációja mátrix és tenzor jelölésben
\
Megjegyezzük, hogy \({\bf Q}\) és \(\lambda_{ij}\) ugyanaz a transzformációs mátrix.
Kétdimenzióban az \({\bf Q}\) és az \(\lambda_{ij}\) definíciója
\\\]
, ami az általánosabb háromdimenziós forma
\\\]
speciális esete.