A proporcionális csak egy módja annak, hogy reagáljunk a rendszer hibájára. Az arányos szabályozással az a probléma, hogy nem képes a tendenciákat felismerni és azokhoz igazodni. Ez az integrálszabályozás feladata.
A 6. ábra bal oldalán egy másik példa grafikon a rendszer hibájának időbeli változásáról. Ez ismét lehet egy robot távolsága egy tárgytól, vagy lehet folyadékszint egy tartályban, vagy a hőmérséklet egy gyári sütőben. Lehet, hogy a célpont, amelyet a robot követ, folyamatosan távolodik a robottól olyan sebességgel, amelyet a robot nem tud utolérni. Talán a sütő ajtajának tömítése kopott; talán a tartályból szokatlanul nagy a folyadékszívás. Az okoktól függetlenül, mivel az arányos robotot nem úgy tervezték, hogy reagáljon a tendenciákra, nem tudja észlelni és korrigálni a problémát. Itt jön a képbe az integrálszabályozás.
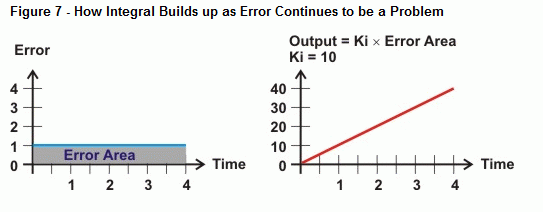
Az integrál a hibaértékek és az időtengely közötti területet méri. Ha a hiba nem tér vissza nullára, a hiba területe egyre nagyobb és nagyobb lesz. A 6. ábra jobb oldala mutatja, hogy az integrál kimenet hogyan reagálhat egy ilyen tendenciára. Ahogy a hibagörbe és az időtengely közötti terület növekszik, a kimenet ezzel a területtel arányosan növekszik. Ennek eredményeképpen a kimenet egyre erősebben hajtja a működtetőt a hiba kijavítására.
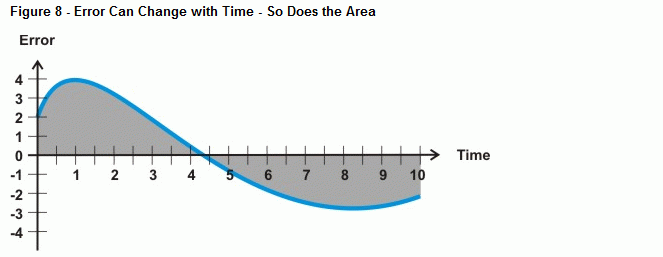
Mi történik tehát, ha a hiba nem egyenes vonal, mint a 8. ábrán látható görbe? Ezt határozza meg az integrálás számtani művelete, a görbe és egy tengely közötti terület. Az integrálszabályozás esetében, ahogy egyre több idő telik el a hibával, a görbe alatti terület növekszik, és így az az érték is, amellyel az integrálszámítás a rendszer hibája ellen hajt. Ha a hibagörbe az időtengely alá esik, a negatív terület felhalmozódása kivonja a pozitív terület felhalmozódását. Megfelelő hangolás esetén az integrálvezérlés segíthet a rendszernek a nulla hiba felé közelíteni.
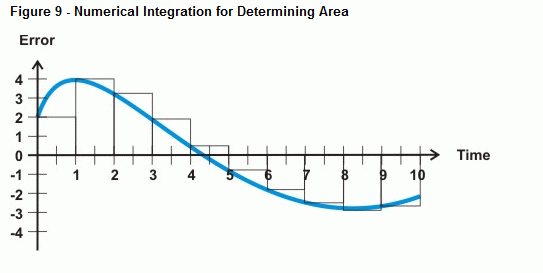
A BASIC Stamp numerikus integrálással közelítheti a görbe alatti hibát. A 9. ábra azt mutatja, hogyan közelítheti a görbe alatti hibát a hibagörbe és az időtengely közötti kis téglalapok területének összeadásával. Az egyes négyzetek területe a hiba és a mérések közötti idő szorzata. Az összes doboz területének összeadásával megkapja a görbe alatti terület közelítő értékét.
Ha a mérések egyenletes távolságra vannak egymástól, akkor az egyes dobozok szélességét nevezheti 1 értéknek. Ez sokkal egyszerűbbé teszi a matematikát, mintha a minták közötti 20 ms-ot, a minták közötti 5 percet vagy bármilyen mintavételi sebességet próbálna figyelembe venni. Ahelyett, hogy megszorozná a hibát a minták közötti időskálával, majd hozzáadná a következő, idővel megszorzott hibához, egyszerűen megszorozhat minden egyes hibamintát 1 idővel. Az eredmény az, hogy az integrálszámításhoz csak a hibamérések folyamatos összegét kell vezetnie. Íme egy példa arra, hogyan lehet ezt PBASIC segítségével elvégezni:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
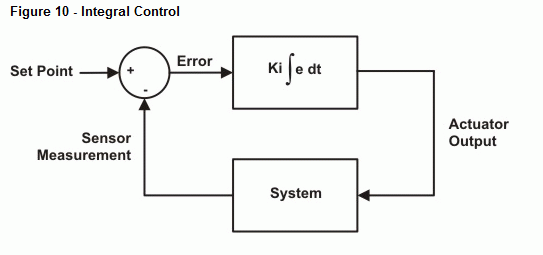
A következő példaprogram numerikus integrálást végez a hibajelen, és ennek megfelelően állítja be a kimenetet. Az arányos szabályozáshoz hasonlóan itt is van egy konstans, amely az integrációs kimenetet a kívánt értékre skálázza. Az egyszerűség kedvéért ismét a 10-es értéket használjuk Ki esetében. A 10. ábra a szabályozási hurok blokkdiagramját mutatja. A Kp ∫ edt kifejezés a Kp és a hiba időbeli integráljának szorzatára utal. Más szóval Kp szorozva a hibagörbe és az időtengely közötti felhalmozott területtel.
Példaprogram – IntegralAlgorithm.bs2
- Adja be, mentse el és futtassa az IntegralAlgorithm.bs2.
- Ezt az értéksorozatot adja be a Debug Terminal átviteli ablaklapjába: 3 3 3 3 3 3 3 3 3. Figyelje meg, hogy az integrál kimenete minden egyes alkalommal, amikor a 3 ismétlődik, egyre nagyobb lesz. Ez az integrál feladata, hogy felismerje a tendenciákat, és szükség szerint növelje a meghajtást a korrekció érdekében.
- Most próbáld ki ezt a sorozatot: 1 2 3 4 5 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0. A görbe alatti terület 0, mivel a negatív terület megegyezik a pozitív területtel. Erre fog jutni az integrálszámítás is, amikor befejeztük a sorozat beírását.
' IntegralAlgorithm.bs2' Demonstrates how integral control influences error correction' in a feedback loop. ' {$STAMP BS2}' {$PBASIC 2.5} SetPoint CON 0 ' Set pointKi CON 10 ' Integral constant Current CON 0 ' Array index for current errorAccumulator CON 1 ' Array index for accumulated error sensorInput VAR Word ' Inputerror VAR Word(2) ' Two element error arrayi VAR Word ' Integral termdrive VAR Word ' Output DO DEBUG "Enter sensor input value: " DEBUGIN SDEC sensorInput ' Calculate error. error(Current) = SetPoint - sensorInput ' Calculate integral term. error(Accumulator) = error(Accumulator) + error(Current) i = Ki * error(Accumulator) ' Calculate output. drive = i ' Display values. DEBUG CR, CR, "ERROR", CR, SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR, "INTEGRAL", CR, SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR, "OUTPUT", CR, SDEC ? i, SDEC ? drive, CR, CR LOOP
Hogyan működik az IntegralAlgorithm.bs2
Ez a program egy ProportionalAlgorithm.bs2 program, amelyet úgy módosítottunk, hogy helyette integrálszámítást végezzen. Most már két különböző típusú hibát kell nyomon követni, ezért ott a hibaváltozó tömbje két eleműre bővült. Az error(0) változó az aktuális hibát követi, az error(1) pedig a felhalmozott hibát. A konstansok Current CON 0 és Accumulator CON 1 kicsit értelmesebbé teszik a könyvelést error(current) és error(accumulator) segítségével.
A másik változás, ami történt, hogy a hiba felhalmozása és az integrál kimenet kiszámítása ezzel a két utasítással történik:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
A te sorod – az integrál kimenet szorítása
Amint azt a Debug Terminálba történő ismételt 3 beírásból talán már kiderült, az integrál hajtás kimenete valóban elkezdhet elszaladni. A MIN és MAX operátorokkal megakadályozhatja, hogy az integrál vezérlés túlzásba vigye a kimenetet. Ismételjük meg a szervo offset tevékenységet, és korlátozzuk a kimenetet 650 és 850 között.
- Változtassuk meg a drive = i utasítást drive = i + Offset MIN 650 MAX 850.
- Futtassuk a programot, és ellenőrizzük, hogy az integrál kimenet 650 és 850 közötti értékekre korlátozódik. Próbálja meg ismételten beírni a 2, majd ismételten a -2 értéket.