
A matematika rengeteg fogalommal foglalkozik, amelyek nagyon fontosak, ugyanakkor bonyolultak és időigényesek. A Python azonban biztosítja a teljes értékű SciPy könyvtárat, amely megoldja számunkra ezt a problémát. Ebben a SciPy oktatóanyagban megtanuljuk, hogyan használhatjuk ezt a könyvtárat néhány függvény és azok példái mellett.
Mielőtt továbblépnénk, nézzük meg a cikkben tárgyalt témákat:
- Mi az a SciPy?
- NumPy vs SciPy
- Alcsomagok a SciPy-ben
- Az alapfüggvények
- Speciális függvények
- Integrációs függvények
- Optimalizációs függvények
- Fourier transzformációs függvények
- Signal Process Processing Functions
- Lineáris algebra
- Sparse Eigenvalues
- Spatial Data Structures and Algorithms
- Multidimensional Image Processing Functions
- File IO
So lássunk hozzá. 🙂
A SciPy egy nyílt forráskódú Python könyvtár, amelyet tudományos és matematikai problémák megoldására használnak. A NumPy kiterjesztésre épül, és lehetővé teszi a felhasználó számára az adatok manipulálását és vizualizálását számos magas szintű paranccsal. Mint korábban említettük, a SciPy a NumPy-ra épül, ezért ha a SciPy-t importáljuk, nincs szükség a NumPy importálására.
NumPy vs SciPy
A NumPy és a SciPy egyaránt matematikai és numerikus elemzésekre használt Python könyvtárak. A NumPy tartalmazza a tömbadatokat és az olyan alapvető műveleteket, mint a rendezés, indexelés stb. míg a SciPy az összes numerikus kódot tartalmazza. Bár a NumPy számos olyan függvényt biztosít, amelyek segíthetnek a lineáris algebra, a Fourier-transzformációk stb. megoldásában, a SciPy az a könyvtár, amely valójában ezeknek a függvényeknek a teljes funkcionalitású változatait tartalmazza sok mással együtt. Ha azonban tudományos elemzést végez Python segítségével, akkor a NumPy-t és a SciPy-t is telepítenie kell, mivel a SciPy a NumPy-ra épül.
A SciPy alcsomagjai:
A SciPy számos alcsomaggal rendelkezik különböző tudományos számításokhoz, amelyeket a következő táblázatban mutatunk be:

A részletes leírásért azonban a hivatalos dokumentációt követheti.
Ezeket a csomagokat használatuk előtt kizárólag importálni kell. Például:
from scipy import cluster
Mielőtt részletesen megvizsgálnánk az egyes függvényeket, először nézzük meg azokat a függvényeket, amelyek mind a NumPy-ben, mind a SciPy-ben közösek.
Interakció a NumPy-vel:
A SciPy a NumPy-re épül, ezért a tömbök kezeléséhez magát a NumPy függvényeit is használhatjuk. Ha mélyebben meg akarja ismerni ezeket a függvényeket, egyszerűen használhatja a help(), info() vagy source() függvényeket.
help():
Hogy információt kapjon bármelyik függvényről, használhatja a help() függvényt. Ezt a függvényt kétféleképpen használhatjuk:
- paraméterek nélkül
- paraméterekkel
Itt egy példa, amely mindkét fenti módszert bemutatja:
from scipy import cluster
help(cluster) #with parameter
help() #without parameter
A fenti kód végrehajtásakor az első help() a klaszter almodulra vonatkozó információkat adja vissza. A második help() arra kéri a felhasználót, hogy adja meg bármely modul, kulcsszó stb. nevét, amelyről a felhasználó információt kíván keresni. A függvény végrehajtásának leállításához egyszerűen írja be a ‘quit’ szót, majd nyomja le az Entert.
info():
Ez a függvény a kívánt függvényekről, modulokról stb. ad vissza információkat.
scipy.info(cluster)
source():
A forráskódot csak a Pythonban írt objektumok esetében adja vissza. Ez a függvény nem ad vissza hasznos információt abban az esetben, ha a metódusok vagy objektumok más nyelven íródtak, például C-n. Abban az esetben azonban, ha használni szeretné ezt a függvényt, a következőképpen teheti meg:
scipy.source(cluster)
Speciális függvények:
A SciPy számos speciális függvényt biztosít, amelyeket a matematikai fizikában használnak, például elliptikus, kényelmi függvények, gamma, béta, stb. Az összes függvény megkereséséhez a korábban leírt help() függvényt használhatjuk.
Exponenciális és trigonometrikus függvények:
A SciPy Speciális függvények csomagja számos olyan függvényt biztosít, amelyek segítségével exponenseket találhatunk és trigonometrikus feladatokat oldhatunk meg.
Nézzük meg a következő példát:
PÉLDA:
from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)
KIADÁS:
1000,0
8,0
1,0
0.7071067811865475
A SciPy speciális függvénycsomagjában sok más függvény is megtalálható, amelyeket kipróbálhatsz magadnak.
Integrálfüggvények:
A SciPy számos függvényt biztosít integrálok megoldására. A közönséges differenciálintegrátortól kezdve a trapézszabályok használatáig az integrálok kiszámításához a SciPy az integrálproblémák minden típusának megoldására alkalmas függvények tárháza.
Általános integrálás:
A SciPy egy quad nevű függvényt biztosít egy olyan függvény integráljának kiszámításához, amelynek egy változója van. A határértékek lehetnek ( ) a végtelen határértékek jelölésére. A quad() függvény szintaxisa a következő:
SYNTAX:
quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)
Itt a függvényt az a és b határértékek között integráljuk (lehet végtelen is).
PÉLDA:
from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)
A fenti példában az ‘a’ függvényt a 0, 1 határértékek között értékeljük ki. Ha ezt a kódot végrehajtjuk, a következő kimenetet látjuk.
KIADÁS:
(3.9086503371292665, 4.3394735994897923e-14)
Kettős integrál függvény:
A SciPy biztosítja a dblquad-ot, amely kettős integrálok kiszámítására használható. A kettős integrál, mint azt sokan tudjuk, két valós változóból áll. A dblquad() függvény az integrálandó függvényt veszi paraméterként, valamint 4 másik változót, amelyek a határértékeket és a dy és dx függvényeket határozzák meg.
PÉLDA:
from scipy import integrate
a = lambda y, x: x*y**2
b = lambda x: 1
c = lambda x: -1
integrate.dblquad(a, 0, 2, b, c)
KIVITEL:
-1.3333333333333333333335, 1.480297366166868755e-14)
A SciPy számos más függvényt is biztosít a hármas integrálok, n integrálok, Romberg-integrálok stb. kiértékelésére, amelyeket részletesebben is megvizsgálhatunk. A szükséges függvényekkel kapcsolatos minden részletet a súgófüggvény segítségével tudhat meg.
Optimalizálási függvények:
A scipy.optimize számos gyakran használt optimalizálási algoritmust biztosít, amelyeket a súgófüggvény segítségével ismerhet meg.
Alapvetően a következőkből áll:
- Többváltozós skalárfüggvények korlátlan és korlátozott minimalizálása, azaz minimalizálása (pl. BFGS, Newton Conjugate Gradient, Nelder_mead simplex, stb.)
- Globális optimalizálási rutinok (pl.. differential_evolution, dual_annealing, stb)
- Kisnégyzetminimalizálás és görbeillesztés (pl. least_squares, curve_fit, stb)
- Skaláris egyváltozós függvények minimalizálói és gyökkeresői (pl. minimize_scalar és root_scalar)
- Multivariáns egyenletrendszer megoldók olyan algoritmusokkal, mint a hibrid Powell, Levenberg-Marquardt.
Rosenbrook függvény:
A Rosenbrook függvény ( rosen) a gradiens alapú optimalizációs algoritmusok tesztproblémája. A SciPy-ban a következőképpen van definiálva:

PÉLDA:
import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)
OUTPUT: 7371.039999999999945
Nelder-Mead:
A Nelder-Mead módszer egy numerikus módszer, amelyet gyakran használnak egy függvény min/max értékének megtalálására egy többdimenziós térben. Az alábbi példában a Nelder-Mead algoritmussal együtt a minimalizálás módszerét használjuk.
PÉLDÁZAT:
from scipy import optimize
a =
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x
OUTPUT: array()
Interpolációs függvények:
A numerikus analízis területén az interpoláció új adatpontok konstruálására utal ismert adatpontok halmazán belül. A SciPy könyvtár egy scipy.interpolate nevű alcsomagból áll, amely spline függvényekből és osztályokból, egydimenziós és többdimenziós (egyváltozós és többváltozós) interpolációs osztályokból stb. áll.
Egyváltozós interpoláció:
Az egyváltozós interpoláció alapvetően a görbeillesztés egy olyan területe, amely kétdimenziós adatpontok egy sorára pontos illeszkedést biztosító görbét talál. A SciPy biztosítja az interp1d függvényt, amely felhasználható az egyváltozós interpoláció előállításához.
PÉLDA:
import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()
KIVITEL:
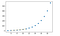
Multivariáns interpoláció:
A multivariáns interpoláció (térbeli interpoláció ) egyfajta interpoláció az egynél több változóból álló függvényeken. A következő példa egy példát mutat be a
Interpolálás egy kétdimenziós rácson az interp2d(x, y, z) függvény használatával alapvetően x, y, z tömböket használ valamilyen függvény interp2d függvény közelítésére. f: “z = f(x, y)” és egy olyan függvényt ad vissza, amelynek hívási módszere spline interpolációt használ az új pontok értékének megtalálására.
PÉLDA:
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()
KIVITEL:

Fourier transzformációs függvények:
A Fourier-analízis olyan módszer, amely azzal foglalkozik, hogy egy függvényt periodikus komponensek összegeként fejezzen ki, és ezekből a komponensekből nyerje vissza a jelet. Az fft függvények egy valós vagy komplex sorozat diszkrét Fourier-transzformációjának visszaadására használhatók.
PÉLDA:
from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)
KIADÁS:
Hasonlóképpen, ennek inverzét is megtalálhatjuk az ifft függvény segítségével az alábbiak szerint:
PÉLDA:
rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)
KIADÁS:
Szignálfeldolgozási függvények:
A jelfeldolgozás olyan jelek elemzésével, módosításával és szintézisével foglalkozik, mint a hang, kép stb. A SciPy biztosít néhány olyan függvényt, amelyek segítségével egy- és kétdimenziós adatokat tervezhetünk, szűrhetünk és interpolálhatunk.
Szűrés:
A jel szűrésével alapvetően a nem kívánt komponenseket távolítjuk el belőle. A rendezett szűrés elvégzéséhez az order_filter függvényt használhatja. Ez a függvény alapvetően egy tömbön végez rendezett szűrést. A függvény szintaxisa a következő:
SYNTAX:
order_filter(a, domain, rank)
a = N dimenziós bemeneti tömb
domain = az `a`-val azonos dimenziószámú maszktömb
rank = Nem negatív szám, amely a rendezés után kiválasztja az elemeket a listából (0 a legkisebb, majd 1…)
PÉLDA:
from scipy import signal
x = np.arange(35).reshape(7, 5)
domain = np.identity(3)
print(x,end='nn')
print(signal.order_filter(x, domain, 1))
OUTPUT:
]
]
Waveforms:
A scipy.signal alcsomag különböző függvényeket is tartalmaz, amelyek hullámformák generálására használhatók. Az egyik ilyen függvény a chirp. Ez a függvény egy frekvenciaszintű koszinuszgenerátor, és a szintaxis a következő:
SYNTAX:
chirp(t, f0, t1, f1, method=’linear’, phi=0, vertex_zero=True)
where,

from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()
OUTPUT:

Lineáris algebra:
A lineáris algebra a lineáris egyenletekkel és azok ábrázolásával foglalkozik vektortér és mátrixok segítségével. A SciPy az ATLAS LAPACK és BLAS könyvtárakra épül, és rendkívül gyors a lineáris algebrával kapcsolatos problémák megoldásában. A numpy.linalg összes függvénye mellett a scipy.linalg számos más fejlett függvényt is biztosít. Továbbá, ha a numpy.linalg-ot nem az ATLAS LAPACK és BLAS támogatással együtt használjuk, a scipy.linalg gyorsabb, mint a numpy.linalg.
Mátrix inverzének megtalálása:
Matematikailag egy A mátrix inverze az a mátrix, ahol ahol a főátló mentén egyesekből álló azonossági mátrix, amelyet B=A-1-nek jelölünk. A SciPy-ben ez az inverz a linalg.inv módszerrel nyerhető ki.
PÉLDÁK:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)
KIVITEL:
]
Determinánsok meghatározása:
A mátrix együtthatóiból számtani úton levezetett értéket nevezzük egy négyzetes mátrix determinánsának. A SciPy-ben ez a det függvény segítségével végezhető el, amelynek szintaxisa a következő:
SYNTAX:
det(a, overwrite_a=False, check_finite=True)
hol,
a : (M, M) Egy négyzetmátrix
overwrite_a( bool, opcionális) : Az a-ban lévő adatok felülírásának engedélyezése
check_finite ( bool, opcionális): Annak ellenőrzése, hogy a bemeneti mátrix csak véges számokból áll-e
PÉLDA:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)
KIVITEL: -5.0
Sparse Eigenvalues:
A sajátértékek a lineáris egyenletekhez kapcsolódó skalárok egy speciális halmaza. Az ARPACK biztosítja, hogy lehetővé teszi a sajátértékek ( sajátvektorok ) meglehetősen gyors megtalálását. Az ARPACK teljes funkcionalitása két magas szintű interfészbe van csomagolva, amelyek a scipy.sparse.linalg.eigs és a scipy.sparse.linalg.eigsh. eigs. Az eigs interfész valós vagy komplex nemszimmetrikus négyzetes mátrixok sajátértékeinek megtalálását teszi lehetővé, míg az eigsh interfész valós szimmetrikus vagy komplex-hermitikus mátrixokhoz tartalmaz interfészeket.
Az eigh függvény egy komplex hermitikus vagy valós szimmetrikus mátrix általános sajátérték-problémáját oldja meg.
EXAMPLE:
from scipy.linalg import eigh
import numpy as np
A = np.array(, , , ])
a, b = eigh(A)
print("Selected eigenvalues :", a)
print("Complex ndarray :", b)
OUTPUT:
Kiválasztott sajátértékek :
komplex ndarray :
]
Térbeli adatszerkezetek és algoritmusok:
A térbeli adatok alapvetően olyan objektumokból állnak, amelyek vonalakból, pontokból, felületekből stb. állnak. A SciPy scipy.spatial csomagja a Qhull könyvtár segítségével képes Voronoi-diagramok, háromszögelések stb. kiszámítására. Ezen kívül tartalmaz KDTree implementációkat a legközelebbi szomszédos pontok lekérdezéséhez.
Delaunay-triangulációk:
Matematikailag a Delaunay-trianguláció egy síkban lévő diszkrét pontok halmazára olyan háromszögelés, amelynél az adott ponthalmazban egyetlen pont sincs bármelyik háromszög kerületi körén belül.
PÉLDA:
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()
KIVITEL:

Multidimenzionális képfeldolgozási függvények:
A képfeldolgozás alapvetően azzal foglalkozik, hogy egy képen műveleteket hajtunk végre az információ kinyerése vagy az eredeti képből egy feljavított kép előállítása érdekében. A scipy.ndimage csomag számos olyan képfeldolgozó és elemző függvényt tartalmaz, amelyeket tetszőleges dimenziójú tömbökkel való munkára terveztek.
Konvolúció és korreláció:
A SciPy számos olyan függvényt biztosít, amelyek lehetővé teszik a képek korrelációját és konvolúcióját.
- A correlate1d függvény használható egydimenziós korreláció kiszámítására egy adott tengely mentén
- A correlate függvény lehetővé teszi bármely adott tömb többdimenziós korrelációját a megadott kernellel
- A convolve1d függvény használható az egydimenziós korreláció kiszámítására.dimenziós konvolúció kiszámítására egy adott tengely mentén
- A convolve függvény lehetővé teszi bármely adott tömb többdimenziós konvolúcióját a megadott kernellel
PÉLDA:
import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)
OUTPUT: array()
File IO:
A scipy.io csomag számos olyan függvényt biztosít, amelyek segítenek a különböző formátumú fájlok kezelésében, mint például MATLAB fájlok, IDL fájlok, Matrix Market fájlok, stb.
A csomag használatához az alábbiak szerint kell importálnunk:
import scipy.io as sio
Az alcsomaggal kapcsolatos teljes körű információkért a File IO hivatalos dokumentumában olvashatunk.
Ezzel elérkeztünk a SciPy Tutorial végére. Remélem, mindent világosan megértettél. Győződjön meg róla, hogy a lehető legtöbbet gyakorol.
Ha további cikkeket szeretne megnézni a piac legtrendibb technológiáiról, mint például a mesterséges intelligencia, a DevOps, az etikus hackelés, akkor az Edureka hivatalos oldalán olvashat.
Nézze meg a sorozat további cikkeit, amelyek a Python és az adattudomány különböző más aspektusait ismertetik.
1. Gépi tanulási osztályozó Pythonban
2. Python Scikit-Learn Cheat Sheet
3. Gépi tanulási eszközök
4. Python könyvtárak az adattudományhoz és a gépi tanuláshoz
5. Gépi tanulási eszközök
. Chatbot Pythonban
6. Python gyűjtemények
7. Python modulok
8. Python fejlesztői készségek
9. Python fejlesztői készségek
. OOPs interjúkérdések és válaszok
10. Önéletrajz egy Python fejlesztő számára
11. Feltáró adatelemzés Pythonban
12. Kígyójáték a Python teknős moduljával
13. Python fejlesztő fizetése
14. Főkomponens-elemzés
15. Python vs C++
16. Scrapy bemutató
17. Web Scraping Pythonnal
18. Legkisebb négyzetek regressziós módszere
19. Jupyter Notebook puskatábla
20. Python alapjai
21. Python mintaprogramok
22. Generátorok Pythonban
23. Dekorátorok Pythonban
24. Python Spyder IDE
25. Mobil alkalmazások a Kivy használatával Pythonban
26. Top 10 legjobb könyv a Python megtanulásához & Gyakorló Python
27. Robot keretrendszer Pythonnal
28. Kígyós játék Pythonban a PyGame segítségével
29. Django interjú kérdések és válaszok
30. Top 10 Python alkalmazás
31. Hash táblák és Hashmaps Pythonban
32. Python 3.8
33. Támogató vektor gép
34. Python oktatóprogram