Less…
![]()
A ![]() sokféle képlete létezik. Ezek közé tartoznak többek között sorozatok, szorzatok, geometriai konstrukciók, határértékek, speciális értékek és pi iterációk.
sokféle képlete létezik. Ezek közé tartoznak többek között sorozatok, szorzatok, geometriai konstrukciók, határértékek, speciális értékek és pi iterációk.
![]() szorosan kapcsolódik a körök és gömbök tulajdonságaihoz. Egy
szorosan kapcsolódik a körök és gömbök tulajdonságaihoz. Egy ![]() sugarú kör esetében, a kerületet és a területet a
sugarú kör esetében, a kerületet és a területet a
|
(1)
|
|||
|
(2)
|
Hasonlóan egy ![]() sugarú gömb esetében, a felület és a térfogat
sugarú gömb esetében, a felület és a térfogat
|
(3)
|
|||
|
(4)
|
Az ![]() pontos képlete az egységtörtek inverz érintőire a Machin-féle formula
pontos képlete az egységtörtek inverz érintőire a Machin-féle formula
|
(5)
|
Három másik Machin-féle képlet létezik,valamint ezer más hasonló képlet, amelyeknek több feltétele van.
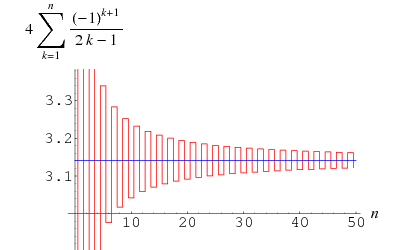
Gregory és Leibniz megtalálta
|
(6)
|
|||
|
(7)
|
(Wells 1986, 50. o.), amelyet Gregory-sorozatként ismerünk, és ![]() beillesztésével kaphatjuk a
beillesztésével kaphatjuk a ![]() Leibniz-sorozatba. Ennek a Gregory-sorozatnak a
Leibniz-sorozatba. Ennek a Gregory-sorozatnak a ![]() -ik tagja utáni hiba nagyobb, mint
-ik tagja utáni hiba nagyobb, mint ![]() , így ez az összeg olyan lassan konvergál, hogy 300 tag nem elegendő a
, így ez az összeg olyan lassan konvergál, hogy 300 tag nem elegendő a ![]() két tizedesjegyig pontos kiszámításához! Átalakítható azonban
két tizedesjegyig pontos kiszámításához! Átalakítható azonban
|
(8)
|
ahol ![]() a Riemann-féle zétafüggvény (Vardi 1991, pp. 157-158; Flajolet és Vardi 1996), így a hiba
a Riemann-féle zétafüggvény (Vardi 1991, pp. 157-158; Flajolet és Vardi 1996), így a hiba ![]() tagok után
tagok után ![]() .
.
A végtelen összegű sorozat Abraham Sharpnak (kb. 1717) a
|
(9)
|
(Smith 1953, 311. o.). További egyszerű sorozatok, amelyekben ![]() jelenik meg:
jelenik meg:
|
(10)
|
|||
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
|||
|
(14)
|
|||
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
(Wells 1986, 53. o.).
Az 1666, Newton egy geometriai konstrukciót használt, hogy levezesse a képletet
|
(18)
|
|||
|
(19)
|
, amelyből kiszámította ![]() (Wells 1986, 50. o.; Borwein et al. 1989; Borwein és Bailey 2003, 105-106. o.). Az együtthatókat az integrálból
(Wells 1986, 50. o.; Borwein et al. 1989; Borwein és Bailey 2003, 105-106. o.). Az együtthatókat az integrálból
|
(20)
|
|||
|
(21)
|
az ![]() 0 körüli sorbővítésével, obtaining
0 körüli sorbővítésével, obtaining
|
(22)
|
(OEIS A054387 és A054388). Az Euler-féle konvergenciajavító transzformáció alkalmazásával
|
(23)
|
|||
|
(24)
|
|||
|
(25)
|
(Beeler et al. 1972, 120. tétel).
Ez megfelel annak, hogy ![]() beillesztjük a
beillesztjük a ![]() ,
,
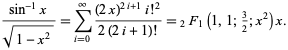 |
(26)
|
A konvergenciajavulás ellenére a sorozat (◇) csak egy biten/termen konvergál. Egy négyzetgyök árán Gosper megjegyezte, hogy ![]() 2 bit/term ad,
2 bit/term ad,
|
(27)
|
és ![]() majdnem 3-at ad.39 bit/term,
majdnem 3-at ad.39 bit/term,
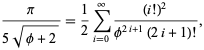 |
(28)
|
ahol ![]() az aranymetszés. Gosper is megkapta
az aranymetszés. Gosper is megkapta
|
(29)
|
A ![]() tüskés algoritmust Rabinowitz és Wagon (1995; Borwein és Bailey 2003, 141-142. o.) adja meg.
tüskés algoritmust Rabinowitz és Wagon (1995; Borwein és Bailey 2003, 141-142. o.) adja meg.
Még meglepőbb, hogy egy zárt formájú kifejezést, amely egy olyan számjegy-kivonatoló algoritmust ad, amely a 16-os bázison ![]() (vagy
(vagy ![]() ) számjegyeket eredményez, Bailey és társai fedeztek fel. (Bailey et al. 1997, Adamchik és Wagon 1997),
) számjegyeket eredményez, Bailey és társai fedeztek fel. (Bailey et al. 1997, Adamchik és Wagon 1997),
|
(30)
|
Ezt a BBP-formulaként ismert képletet a PSLQ algoritmus segítségével fedezték fel (Ferguson et al. 1999), és egyenértékű
|
(31)
|
Az ![]() -re létezik egy sor BBP típusú képlet
-re létezik egy sor BBP típusú képlet ![]() hatványaiban, amelyek első néhány független képlete a következő:
hatványaiban, amelyek első néhány független képlete a következő:
|
(32)
|
|||
|
(33)
|
|||
|
(34)
|
|||
 |
(35)
|
||
 |
(36)
|
||
 |
(37)
|
Hasonlóképpen létezik egy sor BBP típusú formula a ![]()
![]() hatványaiban, amelyek közül az első néhány független formula a következő:
hatványaiban, amelyek közül az első néhány független formula a következő:
|
(38)
|
||||
|
(39)
|
||||
 |
(40)
|
|||
 |
(41)
|
|||
 |
(42)
|
|||
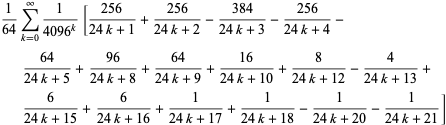 |
(43)
|
|||
 |
(44)
|
|||
 |
(45)
|
|||
 |
(46)
|
|||
 |
(47)
|
|||
 |
(48)
|
F. Bellard megtalálta a gyorsan konvergáló BBP-típusformulát
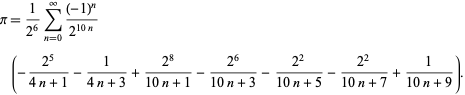 |
(49)
|
A kapcsolódó integrál
|
(50)
|
(Dalzell 1944, 1971; Le Lionnais 1983, p. 22; Borwein, Bailey és Girgensohn 2004, 3. o.; Boros és Moll 2004, 125. o.; Lucas 2005; Borwein et al. 2007, 14. o.). Ezt az integrált K. Mahler már az 1960-as évek közepén megismerte, és egy 1960 novemberében a Sydney-i Egyetemen tartott vizsgán is szerepel (Borwein, Bailey és Girgensohn, 3. o.). Beukers (2000), valamint Boros és Moll (2004, 126. o.) szerint nem világos, hogy létezik-e olyan természetes választású racionális polinom, amelynek integrálja 0 és 1 között ![]() , ahol 333/106 a következő konvergens. Létezik azonban integrál a negyedik konvergensre, nevezetesen
, ahol 333/106 a következő konvergens. Létezik azonban integrál a negyedik konvergensre, nevezetesen
|
(51)
|
(Lucas 2005; Bailey et al. 2007, 219. o.). Valójában Lucas (2005) ad még néhány ilyen integrált.
Backhouse (1995) a
|
(52)
|
|||
|
(53)
|
|||
|
(54)
|
a pozitív egész számok ![]() és
és ![]() esetén és ahol
esetén és ahol ![]() ,
, ![]() , és
, és ![]() racionális konstansok, hogy a
racionális konstansok, hogy a ![]() számos képletét előállítsuk. Különösen, ha
számos képletét előállítsuk. Különösen, ha ![]() , akkor
, akkor ![]() (Lucas 2005).
(Lucas 2005).
Egy hasonló képletet később Ferguson is felfedezett, ami az ilyen formulák kétdimenziós rácsához vezetett, amely e két képlettel generálható a következő módon:
|
(55)
|
bármely komplex ![]() értékre (Adamchik és Wagon), ami a BBP-képletet a
értékre (Adamchik és Wagon), ami a BBP-képletet a ![]() speciális eseteként adja.
speciális eseteként adja.
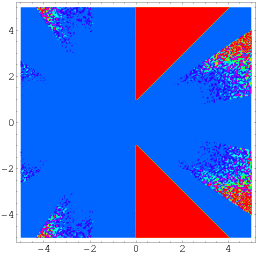
Egy még általánosabb, Wagon-nak köszönhető azonosságot a
 |
(56)
|
(Borwein és Bailey 2003, p. 141), amely a komplex síknak a valós tengely körül szimmetrikusan elhelyezett két háromszögletű részt kizáró tartományára érvényes, amint azt a fenti ábra mutatja.
Az azonosságok talán még furcsább általánosabb osztályát a
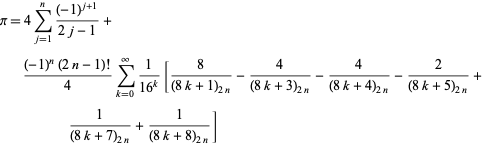 |
(57)
|
ami bármely pozitív egész számra ![]() érvényes, ahol
érvényes, ahol ![]() egy Pochhammer-jel (B. Cloitre, pers. comm.., 2005. január 23.). Még meglepőbb, hogy a 2.
egy Pochhammer-jel (B. Cloitre, pers. comm.., 2005. január 23.). Még meglepőbb, hogy a 2.
természetes logaritmusára is létezik egy szorosan analóg formula.
A 16-os bázisú számjegyű BBP formula és a kapcsolódó formulák felfedezése után hasonló formulákat más bázisokban is vizsgáltak. Borwein, Bailey és Girgensohn (2004) nemrégiben kimutatták, hogy ![]() nem rendelkezik olyan Machin-típusú BBP arctangens-formulával, amely nem bináris, bár ez nem zárja ki, hogy más bázisokban teljesen más séma szerint működnek a számjegy-kivonási algoritmusok.
nem rendelkezik olyan Machin-típusú BBP arctangens-formulával, amely nem bináris, bár ez nem zárja ki, hogy más bázisokban teljesen más séma szerint működnek a számjegy-kivonási algoritmusok.
S. Plouffe kidolgozott egy algoritmust a ![]()
![]() -edik számjegyének kiszámítására bármely bázisban
-edik számjegyének kiszámítására bármely bázisban ![]() lépésben.
lépésben.
A Ramanujan, Catalan és Newton által felállított további azonosságokat Castellanos (1988ab, pp. 86-88) adja meg, köztük több Fibonacci-számok összegét. Ramanujan találta
 |
(58)
|
(Hardy 1923, 1924, 1999, p. 7).
Plouffe (2006) találta a szép képletet
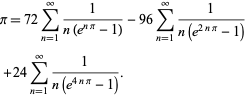 |
(59)
|
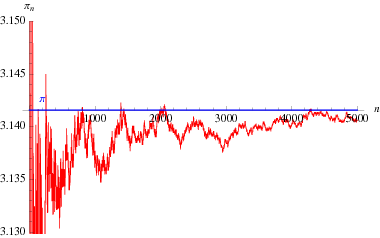
Egy érdekes, Eulernek köszönhető végtelen szorzatos képlet, amely a ![]() és a
és a ![]() egyedik prím
egyedik prím ![]() között áll kapcsolatban:
között áll kapcsolatban:
 |
(60)
|
|||
|
(61)
|
(Blatner 1997, p. 119), amelyet a fenti ábrán a szorzatban szereplő tagok számának függvényében ábrázoltunk.
Az Arkhimédészéhez hasonló módszerrel megbecsülhető a ![]() úgy, hogy egy
úgy, hogy egy ![]() -szögből indulunk ki, majd az ezt követő
-szögből indulunk ki, majd az ezt követő ![]() -szögek területét viszonyítjuk egymáshoz. Legyen
-szögek területét viszonyítjuk egymáshoz. Legyen ![]() a sokszög egyik szegmensének középpontjától számított szög,
a sokszög egyik szegmensének középpontjától számított szög,
|
(62)
|
akkor
|
(63)
|
(Beckmann 1989, pp. 92-94).
Vieta (1593) volt az első, aki pontos kifejezést adott a ![]() -re úgy, hogy a fenti kifejezésben
-re úgy, hogy a fenti kifejezésben ![]() -t vett, így
-t vett, így
|
(64)
|
ami egymásba ágyazott gyökök végtelen szorzatához vezet,
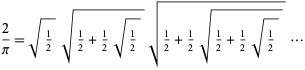 |
(65)
|
(Wells 1986, 50. o.; Beckmann 1989, 95. o.). Ennek a kifejezésnek a konvergenciáját azonban csak Rudio 1892-ben bizonyította be szigorúan.
Egy kapcsolódó képletet a
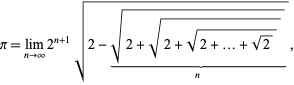 |
(66)
|
mely felírható
|
(67)
|
ahol ![]() az
az
 |
(68)
|
val ![]() (J. Munkhammar, személyes közlés, április 27, 2000). A képlet
(J. Munkhammar, személyes közlés, április 27, 2000). A képlet
 |
(69)
|
is szorosan összefügg.
A ![]() szép képlete a következő:
szép képlete a következő:
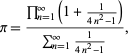 |
(70)
|
ahol a számláló a Wallis-képlet egy formája ![]() , a nevező pedig egy teleszkópos összeg, amelynek összege 1/2, mivel
, a nevező pedig egy teleszkópos összeg, amelynek összege 1/2, mivel
|
(71)
|
(Sondow 1997).
A Wallis-képlet egy speciális esete adja
|
(72)
|
(Wells 1986, 50. o.). Ez a képlet felírható
 |
(73)
|
ahol ![]() egy binomiális együtthatót jelöl, és
egy binomiális együtthatót jelöl, és ![]() a gammafüggvény (Knopp 1990). Euler megkapta
a gammafüggvény (Knopp 1990). Euler megkapta
|
(74)
|
ami a Riemann-féle zétafüggvény ![]() speciális értékéből következik. Hasonló képlet következik
speciális értékéből következik. Hasonló képlet következik ![]() minden pozitív egész számra
minden pozitív egész számra ![]() .
.
A Ramanujan nevéhez fűződő végtelen összeg
|
(75)
|
(Borwein et al. 1989; Borwein és Bailey 2003, 109. o.; Bailey et al.2007, 44. o.). További összegeket ad Ramanujan (1913-14),
|
(76)
|
és
|
(77)
|
|||
|
(78)
|
(Beeler et al. 1972, 139. tétel; Borwein et al. 1989; Borwein és Bailey 2003, 108. o.; Bailey et al. 2007, 44. o.). A (78) egyenlet egy 58-as rendű moduláris azonosságból származik, bár az első levezetést Borwein és Borwein (1987) előtt nem mutatták be. A fenti sorozatok egyaránt adják
|
(79)
|
(Wells 1986, 54. o.) első közelítésként, és termenként kb. 6, illetve 8 tizedesjegyet ad. Ilyen sorozatok léteznek a különböző moduláris invariánsok racionalitása miatt.
A sorozat általános formája
|
(80)
|
ahol ![]() egy bináris kvadratikus forma diszkriminánsa,
egy bináris kvadratikus forma diszkriminánsa, ![]() a j-függvény,
a j-függvény,
|
(81)
|
|||
|
(82)
|
és a ![]() Eisenstein-sorozatok. Egy
Eisenstein-sorozatok. Egy ![]() osztályszámú mezőben
osztályszámú mezőben ![]() töbszörös algebrai egészek állandói
töbszörös algebrai egészek állandói ![]() ,
, ![]() és
és ![]() szerepelnek. A csak egész számokból álló sorozatok közül az a sorozat, amelyik a legrövidebb idő alatt a legtöbb számjegyet adja, megfelel a legnagyobb 1-es osztályszámú
szerepelnek. A csak egész számokból álló sorozatok közül az a sorozat, amelyik a legrövidebb idő alatt a legtöbb számjegyet adja, megfelel a legnagyobb 1-es osztályszámú ![]() diszkriminánsnak, amelyet a Chudnovsky testvérek (1987) fogalmaztak meg. Az itt megjelenő 163 ugyanaz a 163, amely abban is megjelenik, hogy
diszkriminánsnak, amelyet a Chudnovsky testvérek (1987) fogalmaztak meg. Az itt megjelenő 163 ugyanaz a 163, amely abban is megjelenik, hogy ![]() (a Ramanujan-állandó) nagyon közel egész szám. Hasonlóképpen, a
(a Ramanujan-állandó) nagyon közel egész szám. Hasonlóképpen, a ![]() tényező a
tényező a ![]() j-függvény azonosságából származik. A sorozatot a
j-függvény azonosságából származik. A sorozatot a
|
(83)
|
|||
|
(84)
|
(Borwein és Borwein 1993; Beck és Trott; Bailey et al. 2007, 44. o.). Ez a sorozat kifejezésenként pontosan 14 számjegyet ad. Ugyanezt az egyenletet más formában a Chudnovsky testvérek (1987) adták meg, és a Wolfram Language a ![]() kiszámításához használja (Vardi 1991; Wolfram Research),
kiszámításához használja (Vardi 1991; Wolfram Research),
|
(85)
|
hol
|
(86)
|
|||
|
(87)
|
|||
|
(88)
|
A 2. osztályszám (legnagyobb diszkriminancia ![]() ) legjobb képlete
) legjobb képlete
|
(89)
|
hol
|
(90)
|
||||
|
(91)
|
||||
|
(92)
|
(Borwein és Borwein 1993). Ez a sorozat minden további kifejezéssel körülbelül 25 számjegyet ad hozzá. A leggyorsabban konvergáló sorozat a 3. osztályszámhoz ![]() felel meg, és 37-38 számjegyet ad termenként. A leggyorsabban konvergáló 4. osztályú sorozat megfelel
felel meg, és 37-38 számjegyet ad termenként. A leggyorsabban konvergáló 4. osztályú sorozat megfelel ![]() és
és
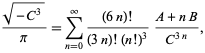 |
(93)
|
hol
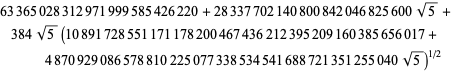 |
(94)
|
||
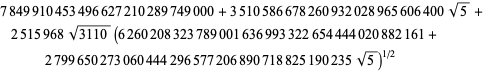 |
(95)
|
||
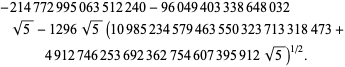 |
(96)
|
Ez termenként 50 számjegyet ad. Borwein és Borwein (1993) kidolgozott egy általános algoritmust ilyen sorozatok generálására tetszőleges osztályszámra.
Ramanujan második és harmadik jegyzetfüzetében talált ![]() sorozatok teljes felsorolását Berndt (1994, pp. 352-354),
sorozatok teljes felsorolását Berndt (1994, pp. 352-354),
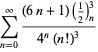 |
(97)
|
||
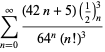 |
(98)
|
||
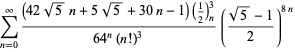 |
(99)
|
||
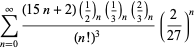 |
(100)
|
||
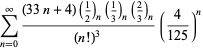 |
(101)
|
||
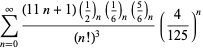 |
(102)
|
||
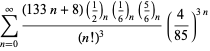 |
(103)
|
||
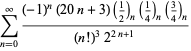 |
(104)
|
||
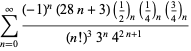 |
(105)
|
||
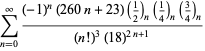 |
(106)
|
||
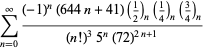 |
(107)
|
||
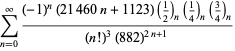 |
(108)
|
||
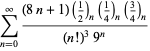 |
(109)
|
||
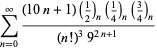 |
(110)
|
||
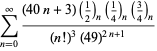 |
(111)
|
||
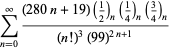 |
(112)
|
||
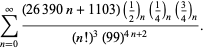 |
(113)
|
Ezeket az egyenleteket először Borwein és Borwein (1987a, pp. 177-187) bizonyította. Borwein és Borwein (1987b, 1988, 1993) más ilyen típusú egyenleteket is bizonyított, Chudnovsky és Chudnovsky (1987) pedig más transzcendens állandókra is talált hasonló egyenleteket (Bailey et al. 2007, pp. 44-45).
Az ilyen típusú független ismert egyenletek teljes listáját a
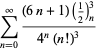 |
(114)
|
||
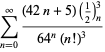 |
(115)
|
||
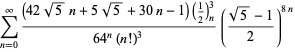 |
(116)
|
||
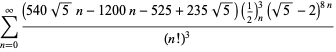 |
(117)
|
||
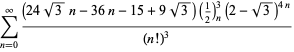 |
(118)
|
for ![]() nem alternatív előjelekkel,
nem alternatív előjelekkel,
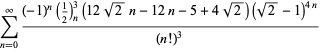 |
(119)
|
||
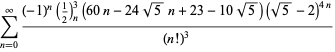 |
(120)
|
||
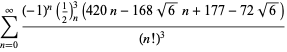 |
(121)
|
||
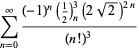 |
(122)
|
for ![]() váltakozó előjelekkel,
váltakozó előjelekkel,
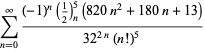 |
(123)
|
||
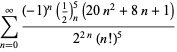 |
(124)
|
for ![]() (Guillera 2002, 2003, 2006),
(Guillera 2002, 2003, 2006),
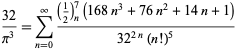 |
(125)
|
ra ![]() (Guillera 2002, 2003, 2006),
(Guillera 2002, 2003, 2006), ![]() -re pedig nem ismert más (Bailey et al. 2007, 45-48. o.).
-re pedig nem ismert más (Bailey et al. 2007, 45-48. o.).
Bellard az egzotikus képletet
 |
(126)
|
where
|
(127)
|
Gasper idézi az eredményt
|
(128)
|
ahol ![]() egy általánosított hipergeometriai függvény, és átalakítja
egy általánosított hipergeometriai függvény, és átalakítja
|
(129)
|
Egy lenyűgöző, Gospernek köszönhető eredményt ad
|
(130)
|
![]() kielégíti az egyenlőtlenséget
kielégíti az egyenlőtlenséget
|
(131)
|
D. Terr (személyes közlés) megjegyezte a különös azonosságot
|
(132)
|
a pi első 9 számjegyének bevonásával.
.