“Az emberek az idő megöléséről beszélnek, míg az idő csendben megöli őket.”
Dion Boucicault – Londoni Biztató (1841)
- Eddig a részecskék kinematikáját és dinamikáját, ezen belül a transzlációs és körmozgást, valamint a részecskék rendszereinek (különösen a merev testek) transzlációs mozgását a rendszer (test) tömegközéppontjának mozgása szempontjából vizsgáltuk. Ez utóbbi esetben el tudjuk képzelni, hogy a külső transzlációs erők tekintetében a test teljes tömege a tömegközéppontban helyezkedik el.
-
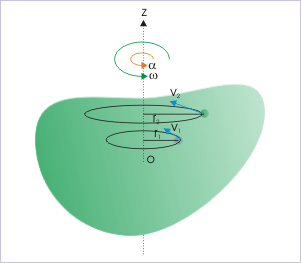A következő lépés egy merev test forgásának vizsgálata egy rögzített forgástengely körül. Megjegyezzük, hogy mivel merev testet tekintünk, a test minden részecskéje a többihez képest rögzített marad. Ez azt jelenti, hogy egy ilyen forgómozgásban minden részecske egy olyan körben mozog, amelynek középpontja a forgástengelyen van. A jobb oldali ábrán a tárgy a z tengely körül forog; a két mintarészecske r1 és r2 sugarú körökben mozog. Ha egy részecske körkörös mozgását a sugarára való közvetlen hivatkozás nélkül is le tudjuk írni, akkor a rendszerben lévő összes részecskét ugyanazzal az egyenletrendszerrel írhatjuk le. Bár a részecskék sugarai különbözőek, szögelfordulásaik azonosak. Ezértszükséges a szögváltozók bevezetése.
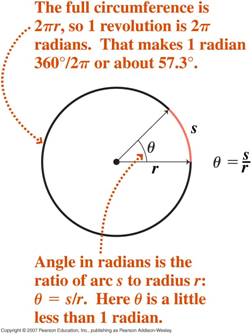
- A szögek radiánmértéke
- Szögsebesség (sebesség) és szöggyorsulás
A szögsebességet és a szöggyorsulást a sebességhez és a gyorsuláshoz hasonlóan határozzuk meg. Mindkettőnek vannak átlagos és pillanatnyi értékei.
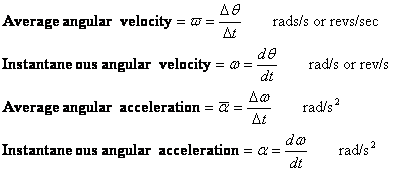
A szöggyorsulás nem azonos a centripetális gyorsulással. A centripetális gyorsulás a sebesség irányának változásából adódik, a szöggyorsulás a sebesség nagyságának változásából (a forgási szögön keresztül).
Pontosan úgy, mint a transzlációs esetben, a szögsebesség és a szögsebesség közötti különbség az irány. A szögsebességnek tartalmaznia kell a kérdéses tengely körüli forgás irányát. Például 10 rad/s az óramutató járásával megegyező irányban az x tengely körül egy szögsebesség, 10 rad/s az x tengely körül egy szögsebesség.
- Rotációs kinematikai egyenletek
A transzlációs kinematikai egyenletekkel közvetlen analógiában a körkörös mozgás egyetlen tengely körül állandó szöggyorsulás mellett a következő négy egyenlettel írható le,
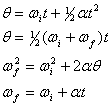
ahol a helyettesítéseket elvégeztük, 
Megjegyezzük, hogy ahogyan +x tetszőlegesen definiálható jobbra, úgy a theta pozitív értéke is definiálható az óramutató járásával megegyezően vagy ellentétesen.
- A szög- és a transzlációs változók közötti kapcsolat
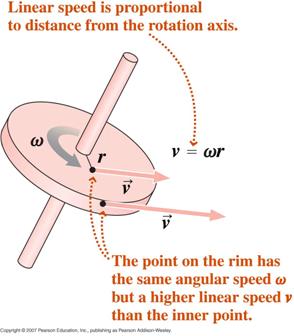A radián mérték definíciójából kiindulva, az idővel való differenciálással megmutathatjuk,
ahol v az érintőleges sebesség és a az érintőleges gyorsulás.
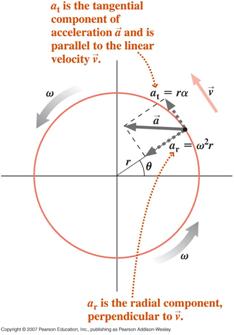
Egy körmozgást végző részecske változó szögsebességgel (nem egyenletes körmozgás) a gyorsulásnak két összetevője lesz, egy érintőleges összetevő a sebességének változó nagysága miatt és egy sugárirányú (centripetális) összetevő a sebességének változó iránya miatt
A részecske nettó gyorsulása e két összetevő vektorösszegéből adódik az alábbiakban jelzett módon.
- Tájékoztatásul…
A több tengely körüli egyidejű forgást a lövedék mozgásához hasonlóan lehet vizsgálni, ahol az 1D transzlációs tárgyalásunkat kiterjesztettük a 2D mozgásra. A repüléstechnikai alkalmazásokban a három tengely körüli forgásokat Roll, Pitch és Yaw néven írják le.
.
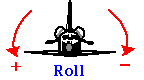
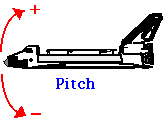
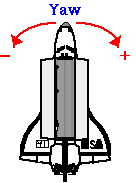
Példa probléma
“Nem akarok halhatatlanságot elérni a munkámmal…Azzal akarom elérni, hogy nem halok meg.”
Woody Allen – Woody Allen és a komédiája (1975)
Dr. C. L. Davis
Fizika Tanszék
Louisville-i Egyetem
E-mail: [email protected]
