
A neurális hálózatok és a matematika elválaszthatatlanok, és valószínűleg ez az, ami a legtöbb embert megijeszti. Túl sok kétkedő megjegyzést hallottam már a Deep Learningről: “Ó, ez túl sok matematika ahhoz, hogy felfogjam”, “Hány vállalat használ valójában Deep Learninget? Inkább megspórolom magamnak az agytornát, és távol maradok ezektől az igényes fogalmaktól.”
De ha belegondolsz, nem is olyan nehéz. Bízz bennem! Ahhoz, hogy megértsük, miért viselkedik egy algoritmus egy bizonyos módon, elengedhetetlen, hogy megértsük, mi történik a színfalak mögött. A komplex gépi tanulási algoritmusokat ma már kényelmesen becsomagolták számunkra, és csak egy függvényhívásnyira vannak tőlünk. Az aktiválási függvények deriváltjai kissé kevésbé nyilvánvaló fogalmak, amelyeket gyakran hajlamosak vagyunk figyelmen kívül hagyni. Ezek azonban nagy teljesítményű algoritmusok alapját képezik, és ha egy kis plusz erőfeszítést fektetünk a megértésükbe, az mindenképpen kifizetődő. E cikk elolvasása után egy lépéssel közelebb kerülsz ahhoz, hogy megfejtsd, mi rejlik a “fekete doboz” homlokzata mögött.
Háttér
A neurális hálózatok különböző aktivációs függvényeket használnak a rejtett és kimeneti rétegekben a tanulási folyamat katalizálására. Néhány általánosan használt aktiválási függvény közé tartozik a Sigmoid és a tanH függvény. A legnépszerűbb aktiválási függvény a ReLU ( Rectified Linear Unit), mivel hatékonyan képes leküzdeni az eltűnő gradiens problémát. Az aktiválási függvények mélyebb betekintése egy másik napra szól. Ma a Sigmoid függvény deriváltja mögötti matematikára fogunk koncentrálni.
Miért fontos az aktiváló függvény deriváltja?
Amint azt valószínűleg tudja, a neurális hálózatokat két lépés hajtja:
- Előre terjedés – A bemeneti adatok átáramlanak a hálózaton, és megkapjuk az előre jelzett kimenetet. Ezt összehasonlítjuk a tényleges kimenettel, és kiszámítjuk a hibát.
- Hátrafelé terjedés – A kiszámított hibát a neurális hálózat paramétereinek frissítésére használjuk az aktiválási függvény deriváltjának segítségével.
A szigmoidfüggvény
A szigmoidfüggvényt, amelyet S alakú görbe jellemez, gyakran a logisztikus függvény speciális eseteként említik. Leginkább olyan esetekben hasznos, amikor kimenetként valószínűséget kell megjósolnunk.
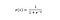
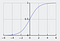
A szigmoid függvény 0 és 1 közötti értékeket ad ki (jogosan, tekintve, hogy valószínűségeket jósol).
A szigmoid derivált
Ez a neurális hálózatok képzését segítő alapvető építőelem a következő formát ölti:


Minden további nélkül, vágjunk bele a deriválásba!
Eljárás 1

Eljárás 2:
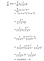
Miért használjuk a származéknak ezt a változatát?
Az előretörési lépésben kiszámítjuk a szigmoid függvényt (σ(x)), és kéznél van az értéke. A derivált kiszámítása során a visszaterjedési lépésben csak annyit kell tennünk, hogy a σ(x) értékét beillesztjük a fent levezetett képletbe, és voilá, máris készen vagyunk!
Ez az, srácok! Köszönjük az olvasást!