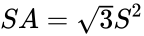Tetrahedron

Szabályos tetraéder
(Kattintson ide a forgó modellért)
Típus	Platonikus szilárdtest
Elemek	F = 4, E = 6 V = 4 (χ = 2)
Alapok oldalanként	4{3}
Schläfli szimbólum	{3,3} és s{2,2}
Wythoff szimbólum	3 | 2 3 | 2 2 2
Coxeter-Dynkin
Szimmetria	Td vagy (*332)
	U01, C15, W1
Tulajdonságok	Szabályos konvex deltaéder
Diéderes szög	70.528779° = arccos(1/3)
3.3.3 (csúcsfigura)	Self-duál (kettős poliéder)
Net

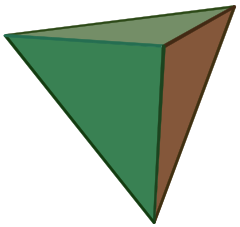
A tetraéder (többes szám: tetraéder) olyan poliéder, amely négy háromszög alakú oldalból áll, amelyek közül három minden csúcson találkozik. A szabályos tetraéder olyan tetraéder, amelyben a négy háromszög szabályos, azaz “egyenlő oldalú”, és a platóni szilárd testek egyike.

A tetraéder a piramis egyik fajtája, amely olyan poliéder, amelynek alapja lapos sokszög, az alapot egy közös ponttal összekötő háromszögalakkal. A tetraéder esetében az alap egy háromszög (a négy oldal bármelyike tekinthető alapnak), ezért a tetraédert háromszögpiramisnak vagy digonális deltaédernek is nevezik.

A szabályos tetraéder képletei

A térfogat

A felület

Template:Commonscat

• F. M. Jackson és Weisstein, Eric W., “Tetraéder” a MathWorldből.
• Weisstein, Eric W., “Tetraéder” from MathWorld.
• Weisstein, Eric W., “Tetraéder” from MathWorld.
• The Uniform Polyhedra
• Tetraéder: Interaktív poliéder modell
• K. J. M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
• Piero della Francesca’s formula for tetrahedron volume at MathPages
• Free paper models of a tetrahedron and many other polyhedra
• An Amazing, Space Filling, Non-regular Tetrahedron, amely egy “rotating ring of tetrahedra”, más néven kaleidociklus leírását is tartalmazza.
• Tetraéder maghálózat Tetraéder szerkezet alkalmazása rugalmas részleges hálós adathálózat létrehozására
• Explicit pontos formulák egy tetszőleges tetraéder tehetetlenségi tenzorára a csúcskoordináták függvényében
• A tetraéder tehetetlenségi tenzora

.