La CA, o corrente alternata, è così chiamata perché la corrente si alterna o capovolge tra due polarità. In altre parole, la corrente (e di conseguenza la tensione) è una funzione del tempo. Questo è fondamentalmente diverso dalla corrente continua che è fissa in polarità e generalmente costante nel tempo. Una fonte di tensione DC da laboratorio, per esempio, mantiene idealmente una tensione fissa attraverso i suoi terminali e non varia nel tempo. Al contrario, mentre una forma d’onda AC oscilla avanti e indietro nel tempo, la sua forma può esibire ampie variazioni che vanno dai percorsi semplici e regolari degli standard di laboratorio come le onde sinusoidali, le onde triangolari e le onde quadre, alle forme d’onda molto più complesse e ondulate prodotte dagli strumenti musicali e dalla voce umana.
L’onda sinusoidale è l’onda più semplice che può essere creata. Rappresenta il moto di un semplice vettore che ruota a velocità costante, come lo spostamento verticale della lancetta dei secondi di un orologio. Un esempio è mostrato nella figura \(\PageIndex{1}). L’asse orizzontale traccia il tempo. Aumenta man mano che ci spostiamo da sinistra a destra (cioè, se il punto A è alla destra del punto B, allora A si verifica più tardi nel tempo rispetto a B). L’asse verticale è rappresentato qui in generale come una percentuale del massimo, ma ordinariamente sarebbe una misura di tensione, corrente, pressione sonora, o simili.
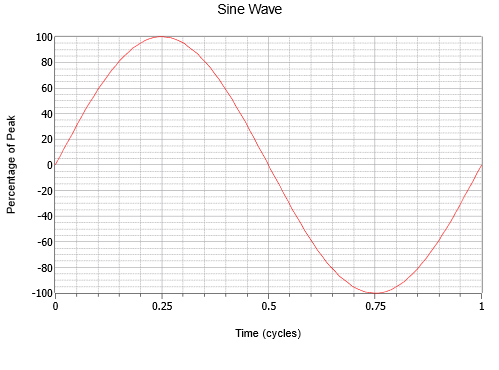
Figura \(\PageIndex{1}): Un’onda sinusoidale.
Nota la variazione regolare che inizia a zero, sale fino a un picco positivo a un quarto del percorso, cade di nuovo a zero a metà percorso, continua fino a un picco negativo a tre quarti, e poi sale di nuovo al punto di partenza. Questo processo poi si ripete. Ogni ripetizione viene chiamata ciclo. Nella Figura \PageIndex{1}, è mostrato un ciclo completo.
Le onde sinusoidali mostrano una simmetria a quarti d’onda. Cioè, ogni quarto (nel tempo) dell’onda è identico a qualsiasi altro se semplicemente lo si capovolge intorno all’asse orizzontale e/o lo si ruota in verticale intorno al suo picco. Il tempo necessario per completare un ciclo è chiamato periodo ed è indicato con il simbolo \(T\) (per il tempo). Il reciproco del periodo è la frequenza, \(f\).
La frequenza indica quanti cicli esistono in un secondo. Per onorare uno dei ricercatori del XIX secolo nel campo, invece di chiamare l’unità “cicli al secondo”, usiamo Hertz, dal nome di Heinrich Hertz e abbreviato Hz. Nella Figura \(\PageIndex{2}}) sono mostrate tre onde sinusoidali con diverse frequenze; l’onda iniziale (verde), un’onda al doppio della frequenza (blu), e una terza alla metà della frequenza o al doppio del periodo (rosso).
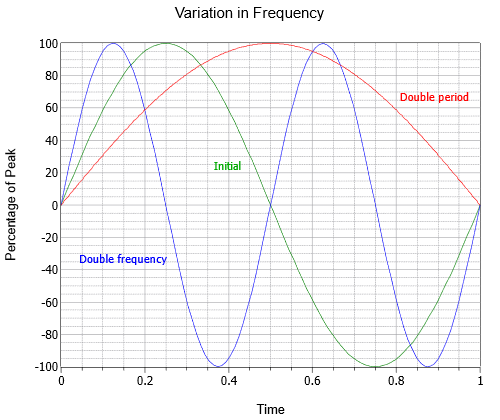
Figura \(\PageIndex{2}): Variazione di frequenza dell’onda sinusoidale.
L’ampiezza (verticale) dell’onda può essere espressa come quantità di picco, che è il cambiamento dalla linea zero centrale fino al valore più positivo. L’ampiezza può anche essere espressa come picco-picco; la distanza dal più negativo al più positivo. Per un’onda sinusoidale questo sarà sempre il doppio del valore di picco, anche se questo potrebbe non essere il caso per altre onde che possono essere asimmetriche. Una serie di tre onde sinusoidali con ampiezze diverse sono mostrate nella figura (\PageIndex{3}). Accanto all’iniziale (verde) ci sono le versioni a doppia ampiezza (blu) e a metà ampiezza (rosso).
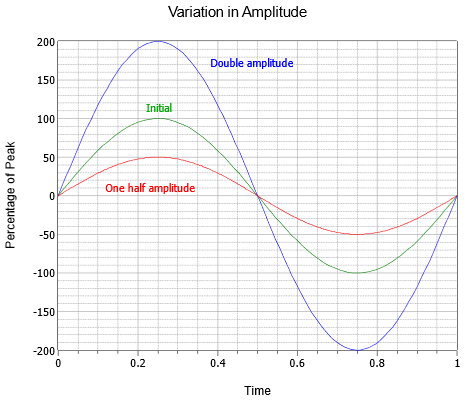
Figura \(\PageIndex{3}}): Variazione dell’ampiezza dell’onda sinusoidale.
Combinando questi parametri, consideriamo la forma d’onda di tensione mostrata nella Figura \(\PageIndex{4}}). Qui vediamo due cicli di una forma d’onda di tensione AC.
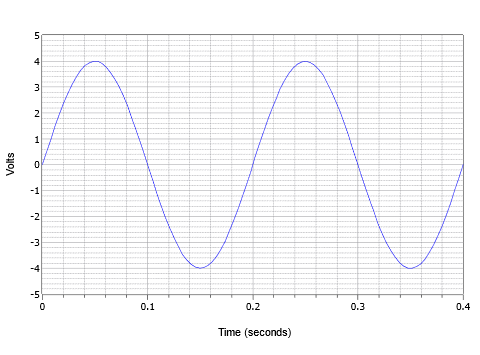
Figura \(\PageIndex{4}): Esempio di sinusoide di base.
Il valore di picco è 4 volt e il valore picco-picco è 8 volt (tipicamente abbreviato come “8 V pp”). Il periodo di un ciclo è di 0,2 secondi, o \(T = 200\) millisecondi. Inoltre, la frequenza, \(f = 1/200\) millisecondi, o 5 Hz (5 cicli in un secondo).
Le forme d’onda AC possono anche essere combinate con un offset DC. Aggiungendo un livello DC positivo si sposta l’onda verticalmente verso l’alto, mentre un livello DC negativo la sposta verticalmente verso il basso. Questo non altera la frequenza o la parte AC dell’ampiezza (anche se i picchi assoluti si sposterebbero del valore DC). La figura \PageIndex{5} mostra l’effetto di vari offset DC. Sopra l’onda iniziale (verde) c’è un’onda altrimenti identica con un offset DC positivo pari al 20% del valore di picco originale (blu). Sotto l’originale c’è una terza onda (rossa) che mostra un offset DC negativo pari alla metà del valore di picco dell’originale.
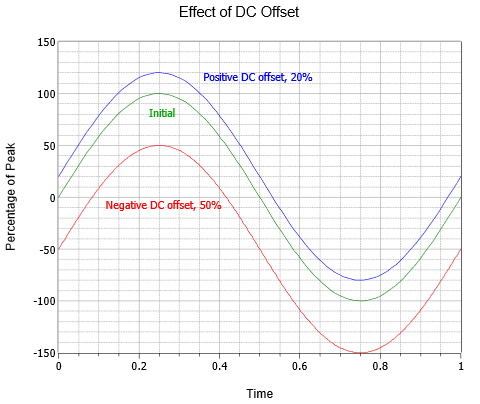
Figura \(\PageIndex{5}): Variazione di offset DC dell’onda sinusoidale.
Inoltre, è possibile per un’onda sinusoidale essere spostata nel tempo rispetto a qualche altra onda sinusoidale o di riferimento. Mentre è possibile indicare questo spostamento come un tempo assoluto, è più comune farlo come uno spostamento di fase, cioè il tempo espresso come una parte del periodo in gradi. Per esempio, se un seno è più avanti di un altro di un quarto del periodo, si dice che è in testa di 90 (^{circ}\) (cioè 1/4 di 360 (^{circ}\). Se è indietro di ½ del periodo, si dice che è in ritardo di 180 (cioè più tardi nel tempo di 1/2 ciclo). Un altro modo di dire questo è che le forme d’onda in testa iniziano prima nel tempo e quindi sono disegnate a sinistra del riferimento, mentre le forme d’onda in ritardo iniziano più tardi nel tempo e sono disegnate a destra.
La figura \(\PageIndex{6}) illustra l’effetto dello spostamento di fase. Si noti che in questo grafico, \(t = 0\) è stato spostato al centro dell’asse orizzontale. La curva centrale è l’onda iniziale, o di riferimento, (verde). A sinistra (rosso) è un’onda che precede l’onda iniziale di un ottavo di ciclo, o 45\(^{circ}\). A destra (blu), c’è un’onda in ritardo della metà, o -22.5\(^{circ}\).
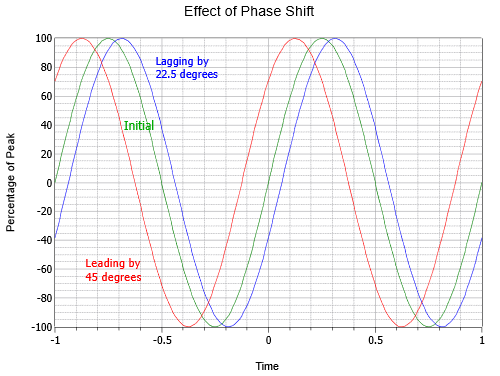
Figura \(\PageIndex{6}}): Variazione di fase dell’onda sinusoidale.
Combinando gli elementi precedenti ci permette di sviluppare un formato generale per un’onda sinusoidale (tensione indicata):
dove
\(v(t)\) è la tensione ad un certo tempo \(t\),
\(V_{DC}\) è l’offset DC, se presente,
\(V_{P}\) è il valore di picco,
\(f\) è la frequenza,
\(\theta\) è lo spostamento di fase (+ se in testa e disegnato a sinistra, – se in coda e disegnato a destra).
Per un esempio veloce e pratico, la forma d’onda mostrata nella figura \(\PageIndex{4}) ha un’ampiezza di 4 volt di picco, una frequenza di 5 Hz, e nessun offset DC o spostamento di fase. Quindi, la sua espressione è \(v(t) = 4 \sin (2 \pi 5 t)\)
Per calcolare uno spostamento di fase, determiniamo prima il differenziale di tempo tra la forma d’onda e il riferimento, che chiameremo \Delta t\). Il riferimento può essere un punto fisso nel tempo (ad esempio, \(t = 0\)) o un’altra forma d’onda. Generalmente, il modo più semplice per farlo è quello di misurare la differenza agli incroci dello zero, assumendo che non ci sia un offset DC. Se c’è un offset, fare la misurazione dove l’attraversamento dello zero è stato spostato (cioè, al livello di offset DC). Una volta trovata la differenza, dividerla per il periodo per rappresentare lo spostamento come una frazione di periodo. Poiché un ciclo rappresenta una rotazione del vettore, o 360 gradi, basta moltiplicare la frazione per 360 gradi per trovare lo spostamento di fase in gradi. Espresso come una formula:
\
Ricordo, se l’onda è spostata a sinistra allora è in testa e positiva, mentre uno spostamento a destra è in ritardo o ritardato nel tempo, e quindi negativo.
Esempio \(\PageIndex{1})
Scrivete l’espressione per la forma d’onda mostrata nella Figura \(\PageIndex{7})
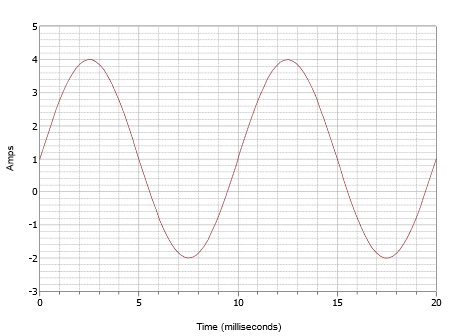
Figura \(\PageIndex{7}): Forma d’onda per l’esempio \(\PageIndex{1}}.
Questa forma d’onda superficialmente può sembrare come quella in Figura \(\PageIndex{4}) ma non lasciatevi ingannare. Prima di tutto, la scala temporale è diversa. Per questa forma d’onda, un ciclo si completa in 10 millisecondi. Pertanto, la frequenza è
\
\
\
Il secondo problema è l’offset DC. Notate che il picco positivo si verifica a 4 ampere mentre il picco negativo si verifica a -2 ampere. Questo indica un valore di picco-picco di 6 ampere. Senza un offset, il picco positivo sarebbe a 3 amp, quindi c’è un offset DC di +1 amp. Il centro verticale della forma d’onda è spostato in alto da 0 amp a +1 amp. Questo punto è a t = 0, quindi non c’è spostamento di fase. L’espressione risultante è:
\
Esempio \(\PageIndex{2})
Scrivi l’espressione per la forma d’onda mostrata nella Figura \(\PageIndex{8}).
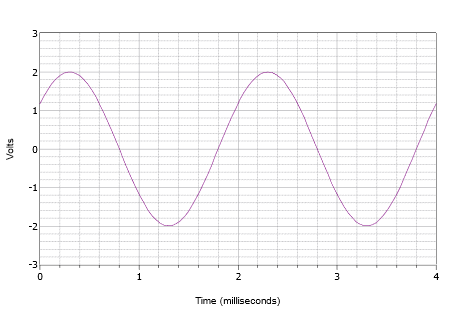
Figura \(\PageIndex{8}): Forma d’onda per l’esempio \(\PageIndex{2}).
Prima di tutto, il picco positivo è 2 volt e il valore picco-picco è 4 volt. Pertanto non c’è alcun offset DC. Il centro verticale dell’onda non inizia a \(t = 0\), quindi ci deve essere uno spostamento di fase. Il valore a \(t = 0\) è 1,2 volt. L’onda colpisce questa stessa ampiezza a \(t = 2\) millisecondi e comincia a ripetere un altro ciclo. Di conseguenza il periodo deve essere di 2 millisecondi. La frequenza è il reciproco di questo valore, e quindi \(f = 500\) Hz.
La forma d’onda è spostata a sinistra, il che indica uno spostamento di fase positivo o iniziale. Se esaminiamo il secondo ciclo, vediamo che colpisce zero volt a 1,8 millisecondi. Quindi lo spostamento è di 0,2 millisecondi. Espresso in gradi questo è:
\
\
\
L’espressione finale è:
\
Esempio \(\PageIndex{3})
Disegna la forma d’onda corrispondente alla seguente espressione.
Prima di tutto, notate che l’offset di -3 volt spinge il picco positivo giù da 5 volt a 2 volt, e il picco negativo giù da -5 volt a -8 volt. La frequenza di 40 kHz detta un periodo di:
Lo spostamento di fase di -72\(^{\circ}}) rappresenta 72/360, o 0,2 cicli. Questo corrisponde ad un ritardo di tempo (spostato a destra perché è negativo) di 0,2 volte 25 \mu\s, o 5 \mu\s.
Inizialmente, è spesso meglio costruire il grafico attraverso una serie di passi discreti piuttosto che cercare di disegnare tutto in una volta. Per prima cosa, disegnate una sinusoide con un’ampiezza di picco di 5 volt e un periodo di 25 \mu\. Ora, spingete la forma d’onda verso il basso di 3 volt in modo che il picco positivo sia solo 2 volt e il picco negativo sia a -8 volt. Infine, spingi la forma d’onda appena spostata a destra di 5 \mu\. Il risultato è mostrato nella figura \(\PageIndex{9}).
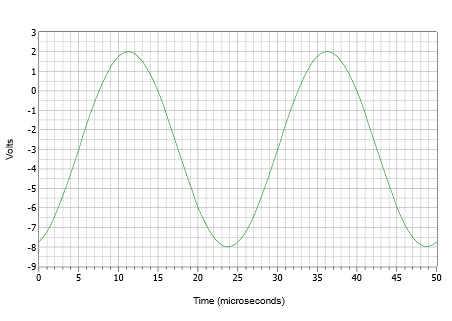
Figura \(\PageIndex{9}): Forma d’onda per l’esempio \(\PageIndex{3}).
1.2.1: Misure di laboratorio
In laboratorio, si usa un generatore di funzioni per generare sinusoidi e altre forme d’onda. Questi dispositivi permettono un controllo preciso sia dell’ampiezza che della frequenza dell’onda insieme all’aggiunta di un offset DC, se desiderato. Un esempio è mostrato nella Figura \(\PageIndex{10}). Lo strumento di misura corrispondente è l’oscilloscopio, o semplicemente oscilloscopio, in breve.

Figura \(\PageIndex{10}): Generatore di segnali da laboratorio.
L’oscilloscopio è forse il dispositivo di misurazione più utile e versatile in laboratorio. Tipicamente, sono dotati di due o quattro canali di ingresso, anche se ne sono possibili altri. Ogni canale di ingresso ha la propria regolazione della sensibilità e tutti i canali condividono un riferimento temporale comune. Il display disegna le forme d’onda nello stesso modo di quelle viste nelle figure \(\PageIndex{1}) – \(\PageIndex{9}). Inoltre, possono tracciare una tensione contro un’altra (modalità X – Y). Gli oscilloscopi moderni hanno caratteristiche aggiuntive come la misurazione automatica di frequenza, ampiezza, spostamento di fase, ecc, misure basate sul cursore, e la capacità di salvare le immagini del display come file grafici. Un esempio di un oscilloscopio digitale a quattro canali è mostrato nella Figura \(\PageIndex{11}\).

Figura \(\PageIndex{11}): Un oscilloscopio digitale.
1.2.2: Simboli schematici
Per quanto riguarda gli schemi, i simboli per le sorgenti di tensione e corrente AC sono mostrati nella figura \(\PageIndex{12}). I segni di polarità e direzione non sono assoluti; dopo tutto, si tratta di sorgenti di corrente alternata la cui polarità e direzione si invertono avanti e indietro. I marcatori sono invece usati per stabilire un riferimento temporale, specialmente nei circuiti che impiegano sorgenti multiple.
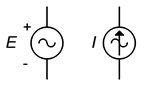
Figura \(\PageIndex{12}): Simboli schematici per la sorgente di tensione AC (sinistra) e la sorgente di corrente (destra).
Va ricordato che negare una sorgente equivale a invertire la sua polarità. Questo era vero per le sorgenti DC e rimane vero per le sorgenti AC. Questo è illustrato nella figura \(\PageIndex{13}). A volte invertire o negare la sorgente renderà l’analisi un po’ più ovvia o più facile da visualizzare.
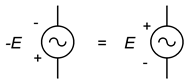
Figura \(\PageIndex{13}\: Equivalenza polarità/segno.
Esempio \(\PageIndex{4})
Assumiamo che un oscilloscopio visualizzi due onde come mostrato nella figura \(\PageIndex{14}). Determinare lo spostamento di fase della forma d’onda più piccola di 20 volt di picco (blu) rispetto alla forma d’onda più grande di 25 volt di picco (rossa).
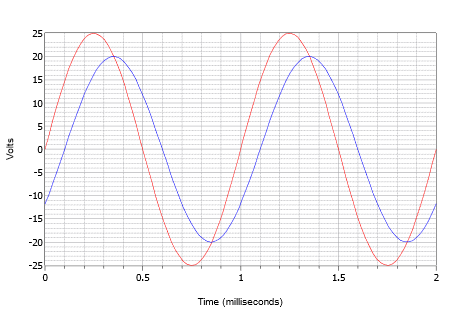
Figura \(\PageIndex{14}}: Forme d’onda per l’esempio \(\PageIndex{4}).
Primo, nota che nessuna delle due onde mostra un offset DC. Se una o entrambe avessero un offset, l’onda o le onde dovrebbero essere spostate verticalmente in modo che i loro normali punti di incrocio dello zero siano allo stesso livello. Misurando l’una o l’altra onda, si trova che il periodo è di 1 millisecondo. Lo spostamento del tempo può essere trovato più facilmente in uno qualsiasi degli incroci dello zero (ci sono quattro posizioni tra cui scegliere). Il ritardo è una piccola deviazione, o 0,1 millisecondi, con l’onda più piccola ritardata nel tempo, o in ritardo sull’onda più grande. Questo indica uno spostamento di fase negativo.
\
\
\
1.2.3: Seni e Coseni
Ci sono una manciata di spostamenti di fase specifici che meritano un’occhiata più da vicino. Se una sinusoide è invertita, cioè capovolta, è indistinguibile da una sinusoide che è stata spostata di +180 o -180 gradi. In altre parole, tale onda può essere scritta in tre modi diversi: \(- \sin (2 \pi ft)\), \(\sin (2 \pi ft – 180^{\circ})\), o \(\sin (2 \pi ft + 180^{\circ})\). Inoltre, se un’onda sinusoidale è spostata di +90 gradi (cioè, avanti e a sinistra), può anche essere indicata come un’onda cosinusoidale. Così \(\sin (2 \pi ft + 90^{\circ}) = \ cos (2 \pi ft)\). Infine, se un’onda sinusoidale è spostata di -90 gradi (cioè, in ritardo e a destra), si può parlare di un’onda cosinusoidale negativa o invertita. Così \(\sin (2 \pi ft – 90^{circ}) = – \cos (2 \pi ft)\). Le relazioni di queste quattro onde sono illustrate nella Figura \PageIndex{15}.
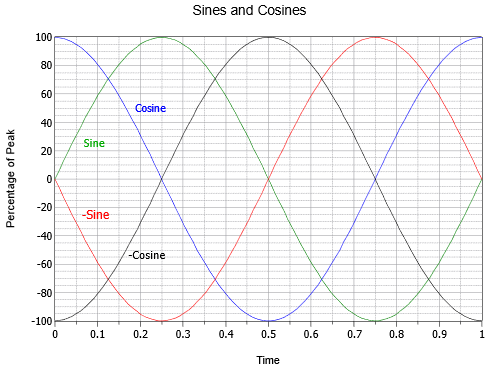
Figura \PageIndex{15}: Relazioni temporali tra seni e coseni.
Va anche notato che l’onda coseno rappresenta la prima derivata, o pendenza, dell’onda sinusoidale. Come si può ricordare da altri studi, la pendenza o “ripidità” di una linea è il rapporto tra il cambiamento verticale e il cambiamento orizzontale, a volte chiamato “l’aumento sulla corsa”. Per una tensione, sarebbe il cambiamento di tensione sul cambiamento di tempo, o \(\Delta V/ \Delta t\). Per una curva liscia e in continuo cambiamento come un’onda sinusoidale, la pendenza in un dato punto è definita correttamente come la derivata prima, o \(dv/dt\) in questo caso. Per verificare visivamente che questo è vero, nota che la parte più ripida della sinusoide (verde) è dove attraversa l’ampiezza zero. Quando attraversa lo zero mentre si muove in positivo (a \(t = 0\) o \(t = 1\) nella figura \(\PageIndex{15}\), il coseno (blu) è al suo picco positivo. Quando il seno attraversa lo zero mentre si muove in negativo (a \(t = 0.5\)), il coseno è al suo picco negativo. Inoltre, l’onda sinusoidale è piatta con una pendenza di zero ai suoi picchi positivi e negativi (a \(t = 0.25\) e \(t = 0.75\), rispettivamente), e in quei momenti l’ampiezza del coseno è anche zero. È anche vero che il seno è la pendenza del coseno negativo, il coseno negativo è la pendenza del seno negativo, e il seno negativo è la pendenza del coseno. Spostandoci in senso inverso, possiamo dire che l’antiderivata (integrale indefinito) di un’onda coseno è un’onda seno, l’integrale di un’onda seno è un’onda coseno negativo, e così via. Queste relazioni si dimostreranno molto utili quando rivolgeremo la nostra attenzione alla risposta dei condensatori e degli induttori nei circuiti AC.
1.2.4: RMS – Root Mean Square Measurement
Insieme al picco e al picco-picco, l’ampiezza può essere data come valore RMS (Root Mean Square). Infatti, se il picco o il picco-picco non è specificato, si assume che la misura sia RMS. L’RMS è un calcolo speciale usato per trovare la potenza DC equivalente (molto comune, per esempio, con gli amplificatori di potenza audio). In altre parole, se siamo interessati a trovare la potenza in un resistore, il calcolo deve essere eseguito utilizzando i valori RMS per la tensione o la corrente, non i valori di picco o picco-picco. In caso contrario, si otterranno potenze errate. Questo è vero indipendentemente dalla forma d’onda; che sia un’onda sinusoidale, triangolare o le onde complesse dei segnali musicali. Se una tensione è specificata come RMS, può essere trattata per i calcoli di potenza proprio come una tensione DC di dimensioni equivalenti. Per esempio, una sinusoide RMS di 1 volt produrrà la stessa dissipazione di potenza e lo stesso riscaldamento in un dato resistore di 1 volt DC. Per questo motivo, l’RMS è talvolta indicato come il valore effettivo (cioè, il valore DC effettivo).
Il nome root-mean-square descrive il processo di determinazione del valore effettivo. In primo luogo, ricordiamo che la potenza è proporzionale al quadrato della tensione o della corrente. Quindi, il nostro primo passo sarà quello di squadrare la forma d’onda di ingresso. Naturalmente, la forma d’onda è una funzione del tempo e il suo quadrato darà una nuova forma. A questo punto, dobbiamo trovare il valore medio di questa nuova forma. La ragione di questo è semplice, ma non necessariamente ovvia. I componenti elettrici ed elettronici hanno una massa, e quindi non si riscaldano o raffreddano istantaneamente. Presentano una costante di tempo termica. Pertanto, rispondono all’input medio nel tempo. Anche se potremmo calcolare in qualche modo la “potenza di picco istantanea” in un determinato istante di tempo, essa non rappresenta la potenza DC equivalente. Una volta che abbiamo ottenuto il valore medio di questa forma d’onda al quadrato, il valore DC corrispondente è solo la radice quadrata della media. Il risultato è un valore frazionario tra zero e uno che viene utilizzato come fattore di scala per trasformare un valore di picco in un valore RMS. Il valore sarà unico per la forma d’onda specifica. Cioè, tutte le sinusoidi (indipendentemente dalla fase) hanno lo stesso fattore, tutte le onde triangolari regolari hanno lo stesso fattore, e così via. Poiché ci occupiamo principalmente di sinusoidi, diamo un’occhiata più da vicino alla determinazione del fattore RMS per esse.
Iniziamo con l’espressione di base per un’onda sinusoidale senza offset DC o spostamento di fase, e con un’ampiezza di uno:
\
Il primo passo è quello di squadrare questa forma d’onda. Un’utile identità trigonometrica è
Applicandola alla nostra onda si ottiene:
Questa espressione descrive un’onda cosinica invertita al doppio della frequenza originale e alla metà dell’ampiezza originale, con un offset DC uguale al suo valore di picco. In altre parole, il picco negativo del coseno è a zero e il picco positivo è a 1. Il passo successivo è trovare il valore medio di questo risultato intermedio. La media è uguale all’offset di 0,5. Questo può essere visualizzato come l’area sopra l’offset che riempie perfettamente il “tuffo” sotto l’offset. Il passo finale è quello di prendere la radice quadrata della media. La radice quadrata di 0,5 è uguale a uno sulla radice quadrata di due, o circa 0,707. Quindi il valore RMS è 0,707 volte il picco. In alternativa, si potrebbe dividere il picco per la radice quadrata di due, ovvero circa 1,414. Questo processo è mostrato graficamente nella Figura \(\PageIndex{16}}).
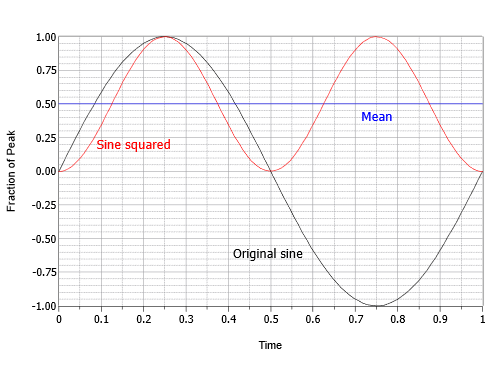
Figura \(\PageIndex{16}}: Processo per trovare il fattore RMS per le sinusoidi.
In sintesi, per le sinusoidi, RMS è sempre il valore di picco per 0,707. Potremmo anche dire che il valore RMS di qualsiasi onda sinusoidale è il suo picco diviso per circa 1,414. Di nuovo, questi rapporti non sarebbero necessariamente veri per le onde non sinusoidali. Dettagli su altre forme comuni possono essere trovati nell’Appendice C. Infine, il rapporto tra il valore di picco e il valore RMS è chiamato rapporto di cresta. Questo è un valore fisso per le onde sinusoidali (di nuovo, circa 1,414), ma può essere oltre 10:1 per alcuni tipi di segnali audio.
1.2.5: Lunghezza d’onda
Un altro elemento di interesse è la velocità di propagazione dell’onda. Questa varia ampiamente. Nel caso della luce nel vuoto (o per approssimazione, una corrente elettrica in un filo), la velocità è di circa 3E8 metri al secondo (cioè, 300.000 km/s) o circa 186.000 miglia al secondo.
Data una velocità e un periodo, possiamo immaginare quanto distano i picchi dell’onda. Questa distanza è chiamata lunghezza d’onda ed è indicata dalla lettera greca lambda \(\lambda\). La lunghezza d’onda è uguale alla velocità divisa per la frequenza, \(\lambda = v/f\). Così, per un altoparlante che produce una sinusoide di 100 Hz, poiché la velocità del suono nell’aria è 344 m/s, allora \(\lambda = 344 m/s \, / \, 100\) Hz, o 3,44 metri (poco più di 11 piedi). Notate che più alta è la frequenza, più corta è la lunghezza d’onda. Inoltre, si noti che più veloce è la velocità, più lunga è la lunghezza d’onda. I calcoli della lunghezza d’onda sono di particolare importanza nel campo delle telecomunicazioni e dell’acustica.