Cinematica rotazionale - Fisica 298

“Gli uomini parlano di uccidere il tempo, mentre il tempo li uccide tranquillamente”
Dion Boucicault – London Assurance (1841)

Fino ad oggi abbiamo considerato la cinematica e la dinamica delle particelle, compreso il moto traslazionale e circolare, nonché il moto traslazionale di sistemi di particelle (in particolare corpi rigidi) in termini di moto del centro di massa del sistema (corpo). In quest’ultimo caso possiamo immaginare che tutta la massa dell’oggetto si trovi nel centro di massa per quanto riguarda le forze traslazionali esterne.

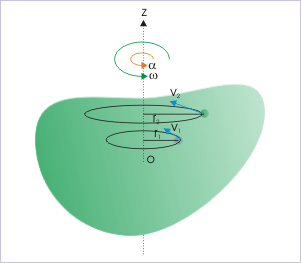Il passo successivo è considerare la rotazione di un corpo rigido intorno a un asse di rotazione fisso. Si noti che, poiché stiamo considerando un corpo rigido, ogni particella del corpo rimane fissa rispetto alle altre. Questo significa che in un tale moto rotatorio ogni particella si muove in un cerchio il cui centro giace sull’asse di rotazione. Nel diagramma a destra l’oggetto ruota intorno all’asse z; le due particelle campione si muovono in cerchi di raggio r1 e r2. Se possiamo descrivere il moto circolare di una particella, senza riferimento diretto al suo raggio, allora tutte le particelle del sistema saranno descritte dallo stesso insieme di equazioni. Anche se i raggi delle particelle sono diversi, le loro rotazioni angolari sono identiche. Perciò è necessario introdurre variabili angolari.

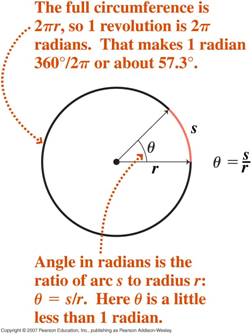
Misura radiante degli angoli

Velocità angolare e accelerazione angolare

Velocità angolare e accelerazione angolare sono definite in modo simile a velocità e accelerazione. Ci sono valori medi e istantanei di ciascuno.

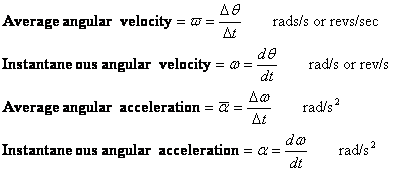
L’accelerazione angolare non è la stessa dell’accelerazione centripeta. L’accelerazione centripeta è dovuta a un cambiamento nella direzione della velocità, l’accelerazione angolare è dovuta a un cambiamento nella grandezza della velocità (attraverso l’angolo di rotazione).

Esattamente come nel caso traslazionale, la differenza tra velocità angolare e velocità angolare è la direzione. La velocità angolare deve includere un senso di rotazione intorno all’asse in questione. Per esempio, 10 rad/s in senso orario intorno all’asse x è una velocità angolare, 10 rad/s intorno all’asse x è una velocità angolare.

Equazioni cinematiche rotazionali

Per analogia diretta con le equazioni cinematiche traslazionali, il moto circolare intorno a un singolo asse sotto accelerazione angolare costante può essere descritto dalle seguenti quattro equazioni,

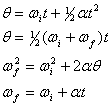
dove abbiamo fatto le sostituzioni,

Nota che così come +x è definito arbitrariamente verso destra, il valore positivo di theta può essere definito come orario o antiorario.

Relazione tra variabili angolari e traslazionali

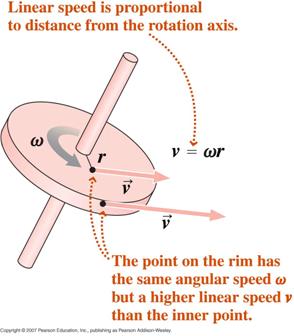Partendo dalla definizione di misura radiante, differenziando rispetto al tempo, possiamo dimostrare che,

dove v è la velocità tangenziale e a l’accelerazione tangenziale.

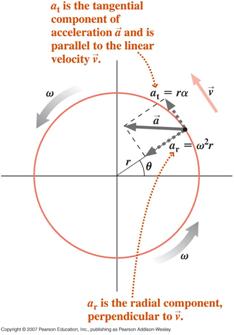
Una particella che esegue un moto circolare, con una velocità angolare variabile (moto circolare non uniforme), sperimenterà due componenti di accelerazione, una componente tangenziale dovuta al cambiamento della grandezza della sua velocità e una componente radiale (centripeta) dovuta al cambiamento della direzione della sua velocità

L’accelerazione netta della particella è la somma vettoriale di queste due componenti come indicato sotto.

Per vostra informazione…

La rotazione simultanea intorno a più di un asse può essere considerata in modo simile al moto del proiettile, dove abbiamo esteso la nostra discussione traslazionale 1D al moto 2D. Nelle applicazioni aeronautiche le rotazioni sui tre assi sono descritte come Roll, Pitch e Yaw.