Come pensare con esponenti e logaritmi

Ecco un trucco per pensare ai problemi che coinvolgono esponenti e logaritmi. Basta fare due domande:

1) Stiamo parlando di input (causa del cambiamento) o di output (il cambiamento effettivo che è avvenuto?)

I logaritmi rivelano gli input che hanno causato la crescita
Gli esponenti trovano il risultato finale della crescita

2) Stiamo parlando della prospettiva del coltivatore o di un osservatore?

e e il log naturale sono dalla prospettiva istante per istante del coltivatore
Base 10, Base 2, ecc. sono misure convenienti per un osservatore umano

Nella mia testa, metto le opzioni in una tabella:

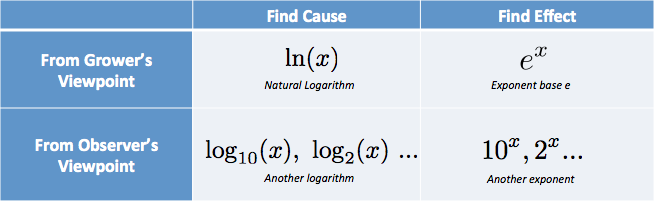
exponent logarithm point of view comparison

Ho pensieri come “Ho bisogno della causa, dalla prospettiva del coltivatore… che è il log naturale”. (Il log naturale è abbreviato con la minuscola LN, dal logarithmus naturalis.)

Sono stato frustrato da lezioni che descrivevano la parte interna della tabella, le funzioni grezze, senza le didascalie che spiegavano quando usarle!

Questo non volerà, facciamo pratica diretta pensando con log ed esponenti.

Scenario: Descrivere la crescita del PIL

Ecco un tipico esempio di crescita:

Dal 2000 al 2010, il PIL degli Stati Uniti è passato da 9,9 trilioni a 14,4 trilioni

Ok, certo, questi numeri mostrano che il cambiamento è avvenuto. Ma probabilmente vogliamo capire la causa: Quale tasso di crescita medio annuo potrebbe spiegare questo cambiamento?

Immediatamente, il mio cervello pensa “logaritmi” perché stiamo lavorando all’indietro dalla crescita al tasso che l’ha causata. Comincio con un pensiero come questo:

${displaystyle{testo{logaritmo del cambiamento} \freccia destra \testo{causa della crescita}$

Un buon inizio, ma cerchiamo di perfezionarlo.

Primo, quale logaritmo dovremmo usare?

Per default, scelgo il logaritmo naturale. La maggior parte degli eventi finisce per essere in termini del coltivatore (non dell’osservatore), e mi piace “cavalcare insieme” all’elemento in crescita per visualizzare ciò che sta accadendo. (I radianti sono simili: misurano gli angoli in termini di chi si muove.)

Domanda successiva: a quale cambiamento applichiamo il logaritmo?

In realtà ci interessa solo il rapporto tra inizio e fine: da 9.900 miliardi a 14.400 miliardi in 10 anni. Questo è lo stesso tasso di crescita che passare da 9,90 a 14,40 dollari nello stesso periodo.

Possiamo affinare il nostro pensiero:

${displaystyle{\testo{logaritmo naturale del rapporto di crescita} \freccia destra \testo{causa della crescita}$

$displaystyle{\ln(\frac{14,4}{9,9}) = .374}$

Ok, la causa era un tasso di .374 o 37,4%. Abbiamo finito?

Non ancora. I logaritmi non sanno quanto tempo è durato un cambiamento (non abbiamo inserito 10 anni, giusto?). Ci danno un tasso come se tutto il cambiamento fosse avvenuto in un unico periodo di tempo.

Il cambiamento potrebbe effettivamente essere un singolo anno di crescita continua del 37,4%, o 2 anni di crescita del 18,7%, o qualche altra combinazione.

Dallo scenario, sappiamo che il cambiamento ha richiesto 10 anni, quindi il tasso deve essere stato:

$\displaystyle{ \testo{rate} = \frac{.374}{10} = .0374 = 3.74\%}$

Dal punto di vista della crescita istantanea e continua, l’economia statunitense è cresciuta del 3.74% all’anno.

Abbiamo finito? Non proprio!

Questo tasso continuo è dal punto di vista del coltivatore, come se stessimo “cavalcando” l’economia mentre cambia. Un banchiere probabilmente si preoccupa della differenza di anno in anno, a misura d’uomo. Possiamo capirlo lasciando la crescita continua per un anno:

${displaystyle{exponent with rate and time} \freccia destra \testo{effetto della crescita} }$

$\displaystyle{e^{\text{rate} \cdot \tempo}} = \testo{crescita}}$

$\displaystyle{e^{.0374 \cdot 1} = 1.0381}$

Il guadagno su base annua è del 3,8%, leggermente superiore al tasso istantaneo del 3,74% dovuto al compounding. Ecco un altro modo di metterla:

Da un istante per istante, una data parte dell’economia sta crescendo del 3,74%, modellato da $e^(.0374 * anni)$
Su una base anno per anno, con gli effetti composti elaborati, l’economia cresce del 3,81%, modellato da $1,0381^anni$

In finanza, possiamo volere il cambiamento anno per anno che può essere paragonato bene con altre tendenze. Nella scienza e nell’ingegneria, preferiamo modellare il comportamento su base istantanea.

Scenario: Descrivere la crescita naturale

Detesto gli esempi artificiosi come “Supponiamo che un batterio raddoppi ogni 24 ore, trova la sua formula di crescita”. Le colonie di batteri si replicano su intervalli umani puliti, e noi aspettiamo un raddoppio esatto?

Uno scenario migliore: “Ehi, ho trovato dei batteri, ho aspettato un’ora, e il grumo è cresciuto da 2,3 grammi a 2,32 grammi. Ora vado a pranzo. Calcola quanto avremo quando tornerò tra 3 ore”

Modelliamo questo. Avremo bisogno di un logaritmo per trovare il tasso di crescita, e poi un esponente per proiettare questa crescita in avanti. Come prima, teniamo tutto in termini di logaritmo naturale per iniziare.

Il fattore di crescita è:

$\displaystyle{{logaritmo del cambiamento} \freccia destra \testo{causa della crescita}$

${displaystyle{\ln(\testo{crescita}) = \ln(2.32/2.3) = .0086 = .86\%}$

Questo è il tasso per un’ora, e il modello generale per proiettare in avanti sarà

${displaystyle{\testo{esponente con tasso e tempo} \freccia destra \testo{effetto della crescita}$

${displaystyle{e^{.0086 \cdot \testo{ore} \freccia destra \testo{effetto della crescita}$

Se iniziamo con 2.32 e cresciamo per 3 ore avremo:

$\displaystyle{2.32 \cdot e^{.0086 \cdot 3} = 2.38}$

Solo per divertimento, quanto tempo manca al raddoppio dei batteri? Immaginate di aspettare che 1 diventi 2:

$\displaystyle{1 \cdot e^{.0086 \cdot \text{hours}} = 2}$

Possiamo meccanicamente prendere il log naturale di entrambi i lati per “annullare l’esponente”, ma pensiamo intuitivamente.

Se 2 è il risultato finale, allora ln(2) è l’input di crescita che ci ha portato lì (qualche tasso × tempo). Sappiamo che il tasso era .0086, quindi il tempo per arrivare a 2 sarebbe:

$\displaystyle{ \testo{ore} = \frac{\ln(2)}{testo{ tasso}} = \frac{.693}{.0086} = 80.58}$

La colonia raddoppierà dopo ~80 ore. (Contenti di non essere rimasti nei paraggi?)

Cosa significa veramente il cambiamento di prospettiva?

Capire se si vuole l’input (causa della crescita) o l’output (risultato della crescita) è abbastanza semplice. Ma come si visualizza la prospettiva del coltivatore?

Immaginiamo di avere dei piccoli lavoratori che stanno costruendo il modello di crescita finale (vedi l’articolo sugli esponenti):

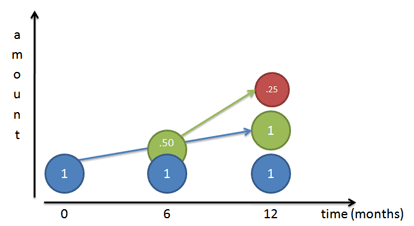
$interesse composto$

Se il nostro tasso di crescita è del 100%, stiamo dicendo al nostro lavoratore iniziale (Mr. Blue) di lavorare costantemente e creare una copia di se stesso al 100% alla fine dell’anno. Se lo seguiamo giorno per giorno, vediamo che finisce una copia di se stesso al 100% (Mr. Green) alla fine dell’anno.

Ma… anche il lavoratore che stava costruendo (Mr. Green) inizia a lavorare. Se Mr. Green appare per la prima volta alla scadenza dei 6 mesi, ha un semestre per lavorare (stesso tasso annuale di Mr. Blue) e costruisce Mr. Red. Naturalmente, Mr. Red finisce per essere fatto a metà, poiché Mr. Green ha solo 6 mesi.

E se Mr. Green si presentasse dopo 4 mesi? Un mese? Un giorno? Un secondo? Se i lavoratori iniziano a crescere immediatamente, otteniamo la curva istante per istante definita da $e^x$:

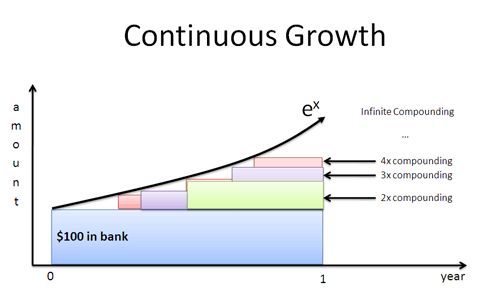
crescita continua

Il log naturale dà un tasso di crescita in termini di prospettiva del singolo lavoratore. Inseriamo quel tasso in $e^x$ per trovare il risultato finale, con tutti i composti inclusi.

Utilizzando altre basi

Passare ad un altro tipo di logaritmo (base 10, base 2, ecc.) significa che stiamo cercando qualche modello nella crescita complessiva, non quello che il singolo lavoratore sta facendo.

Ogni logaritmo pone una domanda quando si vede un cambiamento:

Log base e: Qual è stato il tasso istantaneo seguito da ogni lavoratore?
Log base 2: Quanti raddoppi sono stati necessari?
Log base 10: Quanti 10x sono stati necessari?

Ecco uno scenario da analizzare:

In 30 anni, il numero di transistor sui chip tipici è passato da 1000 a 1 miliardo

Come analizzeresti questo?

I microchip non sono una singola entità che cresce senza problemi nel tempo. Sono edizioni separate, di aziende concorrenti, e indicano una tendenza tecnologica generale.
Siccome non stiamo “cavalcando” un microchip in espansione, usiamo una scala fatta per comodità umana. Raddoppiare è più facile da pensare che decuplicare.

Con questi presupposti otteniamo:

$\displaystyle{\testo{logaritmo del cambiamento} \freccia destra \testo{causa della crescita}$

${displaystyle{{log_2(\frac{1 miliardo}{1000}) = \log_2(\1 milione}) \sim \testo{20 raddoppi}}$

La “causa della crescita” sono stati 20 raddoppi, che sappiamo essere avvenuti in 30 anni. Questa è una media di 2/3 raddoppi all’anno, o 1,5 anni per raddoppio – una bella regola empirica.

Dalla prospettiva del coltivatore, calcoleremmo $ln(\testo{1 miliardo}/1000) / \testo{30 anni} = 46\%$ di crescita continua (un po’ più difficile da relazionare in questo scenario).

Possiamo riassumere la nostra analisi in una tabella:

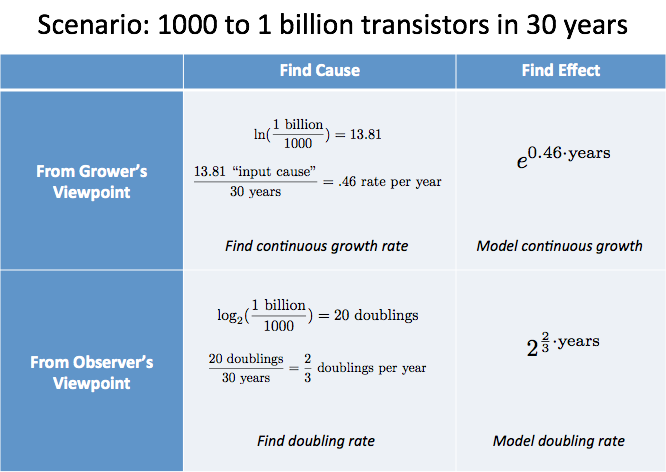
esponenti transistor esempio

Sommario

L’apprendimento consiste nel trovare le didascalie nascoste dietro un concetto. Quando viene usato? Quale punto di vista porta al problema?

La mia interpretazione attuale è che gli esponenti chiedono di causa vs. effetto e di coltivatore vs. osservatore. Ma non abbiamo mai finito; parte del divertimento è vedere come possiamo ricapitolare vecchi concetti.

Felice matematica.

Appendice: La formula del cambio di base

Ecco come pensare al cambio di base. Assumendo un tasso di crescita continuo del 100%,

ln(x) è il tempo per crescere fino a x
ln(2) è il tempo per crescere fino a 2

Siccome abbiamo il tempo per raddoppiare, possiamo vedere quanti “ci starebbero” nel tempo totale per crescere fino a x:

$\displaystyle{\testo{numero di raddoppi da 1 a x} = \frac{\ln(x)}{\ln(2)} = \log_2(x)}$

Per esempio, quanti raddoppi avvengono da 1 a 64?

Bene, ln(64) = 4,158. E ln(2) = .693. Il numero di raddoppi che si adattano è:

$\displaystyle{frac{{ln(64)}{ln(2)} = \frac{4.158}{.693} = 6}$

Nel mondo reale, le calcolatrici possono perdere precisione, quindi usate una funzione log diretta in base 2 se possibile. E naturalmente, possiamo avere un numero frazionario: Passare da 1 alla radice quadrata di 2 è “metà” di un raddoppio, o log2(1,414) = 0,5.

Cambiando in base 10 significa che stiamo contando il numero di 10x-ings che vanno bene:

$\displaystyle{\testo{numero di 10x-ings da 1 a x} = \frac{\ln(x)}{\ln(10)} = \log_{10}(x) }$

Bene, no? Leggi Usare i logaritmi nel mondo reale per altri esempi.

Altri post in questa serie

Guida intuitiva alle funzioni esponenziali & e
Demistificazione del logaritmo naturale (ln)
Guida visiva ai tassi di interesse semplici, composti e continui
Definizioni comuni di e (colorate)
Conoscenza degli esponenti (Perché 0^0 = 1?)
Utilizzare i logaritmi nel mondo reale
Come pensare con esponenti e logaritmi
Comprendere la crescita discreta e continua
Cosa significa veramente un esponente?
Q: Perché e è speciale? (2,718…, non 2, 3,7 o un altro numero?)