
La matematica tratta un numero enorme di concetti che sono molto importanti ma allo stesso tempo, complessi e che richiedono tempo. Tuttavia, Python fornisce la completa libreria SciPy che risolve questo problema per noi. In questo tutorial di SciPy, imparerai come utilizzare questa libreria insieme ad alcune funzioni e ai loro esempi.
Prima di andare avanti, dai un’occhiata a tutti gli argomenti trattati in questo articolo:
- Che cos’è SciPy?
- NumPy vs SciPy
- Sottopacchetti in SciPy
- Funzioni di base
- Funzioni speciali
- Funzioni di integrazione
- Funzioni di ottimizzazione
- Funzioni di trasformata di Fourier
- Signal Processing Functions
- Algebra lineare
- Gli autovalori sparsi
- Strutture di dati spaziali e algoritmi
- Funzioni di elaborazione di immagini multidimensionali
- File IO
Partiamo. 🙂
SciPy è una libreria Python open-source usata per risolvere problemi scientifici e matematici. È costruita sull’estensione NumPy e permette all’utente di manipolare e visualizzare i dati con una vasta gamma di comandi di alto livello. Come menzionato prima, SciPy si basa su NumPy e quindi se importi SciPy, non c’è bisogno di importare NumPy.
NumPy vs SciPy
Sia NumPy che SciPy sono librerie Python usate per l’analisi matematica e numerica. NumPy contiene dati di array e operazioni di base come l’ordinamento, l’indicizzazione, ecc. mentre SciPy consiste in tutto il codice numerico. Anche se NumPy fornisce un certo numero di funzioni che possono aiutare a risolvere l’algebra lineare, le trasformate di Fourier, ecc, SciPy è la libreria che in realtà contiene versioni complete di queste funzioni insieme a molte altre. Tuttavia, se stai facendo analisi scientifiche usando Python, avrai bisogno di installare sia NumPy che SciPy poiché SciPy si basa su NumPy.
Sottopacchetti in SciPy:
SciPy ha un certo numero di sottopacchetti per vari calcoli scientifici che sono mostrati nella seguente tabella:

Tuttavia, per una descrizione dettagliata, puoi seguire la documentazione ufficiale.
Questi pacchetti devono essere importati esclusivamente prima di utilizzarli. Per esempio:
from scipy import cluster
Prima di esaminare ciascuna di queste funzioni in dettaglio, diamo prima un’occhiata alle funzioni che sono comuni sia in NumPy che in SciPy.
Interazione con NumPy:
SciPy si basa su NumPy e quindi è possibile fare uso delle funzioni NumPy stesse per gestire gli array. Per conoscere a fondo queste funzioni, puoi semplicemente fare uso delle funzioni help(), info() o source().
help():
Per ottenere informazioni su qualsiasi funzione, puoi fare uso della funzione help(). Ci sono due modi in cui questa funzione può essere usata:
- senza parametri
- utilizzando parametri
Ecco un esempio che mostra entrambi i metodi di cui sopra:
from scipy import cluster
help(cluster) #with parameter
help() #without parameter
Quando si esegue il codice sopra, la prima help() restituisce le informazioni sul sottomodulo del cluster. La seconda help() chiede all’utente di inserire il nome di qualsiasi modulo, parola chiave, ecc. per cui l’utente desidera cercare informazioni. Per fermare l’esecuzione di questa funzione, digitate semplicemente ‘quit’ e premete invio.
info():
Questa funzione restituisce informazioni sulle funzioni, i moduli, ecc. desiderati.
scipy.info(cluster)
source():
Il codice sorgente viene restituito solo per oggetti scritti in Python. Questa funzione non restituisce informazioni utili nel caso in cui i metodi o gli oggetti siano scritti in qualsiasi altro linguaggio come il C. Tuttavia nel caso in cui vogliate fare uso di questa funzione, potete farlo come segue:
scipy.source(cluster)
Funzioni speciali:
SciPy fornisce una serie di funzioni speciali che sono usate nella fisica matematica come ellittiche, funzioni di convenienza, gamma, beta, ecc. Per cercare tutte le funzioni, puoi fare uso della funzione help() come descritto in precedenza.
Funzioni esponenziali e trigonometriche:
Il pacchetto di funzioni speciali di SciPy fornisce una serie di funzioni attraverso le quali puoi trovare esponenti e risolvere problemi trigonometrici.
Considera il seguente esempio:
EXAMPLE:
from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)
OUTPUT:
1000.0
8.0
1.0
0.7071067811865475
Ci sono molte altre funzioni presenti nel pacchetto di funzioni speciali di SciPy che puoi provare da solo.
Funzioni di integrazione:
SciPy fornisce una serie di funzioni per risolvere integrali. Spaziando dall’integratore differenziale ordinario all’uso delle regole trapezoidali per calcolare gli integrali, SciPy è un magazzino di funzioni per risolvere tutti i tipi di problemi di integrazione.
Integrazione generale:
SiPy fornisce una funzione chiamata quad per calcolare l’integrale di una funzione che ha una variabile. I limiti possono essere ( ) per indicare limiti infiniti. La sintassi della funzione quad() è la seguente:
SYNTAX:
quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)
Qui, la funzione sarà integrata tra i limiti a e b (può anche essere infinito).
ESEMPIO:
from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)
Nell’esempio precedente, la funzione ‘a’ viene valutata tra i limiti 0, 1. Quando questo codice viene eseguito, si vedrà il seguente output.
OUTPUT:
(3.9086503371292665, 4.3394735994897923e-14)
Funzione integrale doppio:
SciPy fornisce dblquad che può essere usato per calcolare integrali doppi. Un integrale doppio, come molti di noi sanno, consiste di due variabili reali. La funzione dblquad() prende come parametro la funzione da integrare insieme ad altre 4 variabili che definiscono i limiti e le funzioni dy e dx.
EXAMPLE:
from scipy import integrate
a = lambda y, x: x*y**2
b = lambda x: 1
c = lambda x: -1
integrate.dblquad(a, 0, 2, b, c)
OUTPUT:
-1.33333333333335, 1.4802973661668755e-14)
SciPy fornisce varie altre funzioni per valutare integrali tripli, integrali n, integrali di Romberg, ecc. che potete esplorare ulteriormente in dettaglio. Per trovare tutti i dettagli sulle funzioni richieste, usate la funzione help.
Funzioni di ottimizzazione:
Lo scipy.optimize fornisce una serie di algoritmi di ottimizzazione comunemente usati che possono essere visti usando la funzione help.
Fondamentalmente consiste nei seguenti:
- Minimizzazione non vincolata e vincolata di funzioni scalari multivariate cioè minimizzare (es. BFGS, Newton Conjugate Gradient, Nelder_mead simplex, ecc)
- Routine di ottimizzazione globale (es. differential_evolution, dual_annealing, ecc)
- Minimizzazione dei minimi quadrati e adattamento delle curve (es. least_squares, curve_fit, ecc)
- Minimizzatori di funzioni univariate scalari e root finder (es. minimize_scalar e root_scalar)
- Solutori di sistemi di equazioni multivariate usando algoritmi come l’ibrido Powell, Levenberg-Marquardt.
Funzione Rosenbrook:
La funzione Rosenbrook ( rosen) è un problema di test usato per algoritmi di ottimizzazione basati sul gradiente. È definita come segue in SciPy:

EXAMPLE:
import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)
OUTPUT: 7371.0399999999945
Nelder-Mead:
Il metodo Nelder-Mead è un metodo numerico spesso usato per trovare il min/max di una funzione in uno spazio multidimensionale. Nell’esempio seguente, il metodo minimize è usato insieme all’algoritmo Nelder-Mead.
EXAMPLE:
from scipy import optimize
a =
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x
OUTPUT: array()
Funzioni di interpolazione:
Nel campo dell’analisi numerica, l’interpolazione si riferisce alla costruzione di nuovi punti dati in un insieme di punti dati noti. La libreria SciPy consiste in un sottopacchetto chiamato scipy.interpolate che consiste in funzioni e classi spline, classi di interpolazione unidimensionale e multidimensionale (univariata e multivariata), ecc.
Interpolazione univariata:
L’interpolazione univariata è fondamentalmente un’area di curve-fitting che trova la curva che fornisce un adattamento esatto a una serie di punti dati bidimensionali. SciPy fornisce la funzione interp1d che può essere utilizzata per produrre interpolazioni univariate.
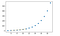
EXAMPLE:
import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()
OUTPUT:
Interpolazione multivariata:
L’interpolazione multivariata (interpolazione spaziale) è un tipo di interpolazione su funzioni che consistono di più di una variabile. L’esempio seguente dimostra un esempio di
Interpolazione su una griglia 2-D usando la funzione interp2d(x, y, z) fondamentalmente userà gli array x, y, z per approssimare qualche funzione interp2d. f: “z = f(x, y)” e restituisce una funzione il cui metodo di chiamata usa l’interpolazione spline per trovare il valore dei nuovi punti.
ESEMPIO:
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()
OUTPUT:

Funzioni di trasformata di Fourier:
L’analisi di Fourier è un metodo che si occupa di esprimere una funzione come somma di componenti periodiche e recuperare il segnale da tali componenti. Le funzioni fft possono essere utilizzate per restituire la trasformata discreta di Fourier di una sequenza reale o complessa.
EXAMPLE:
from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)
OUTPUT:
Similmente, è possibile trovare l’inverso di questo utilizzando la funzione ifft come segue:
EXAMPLE:
rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)
OUTPUT:
Funzioni di elaborazione dei segnali:
L’elaborazione dei segnali si occupa di analizzare, modificare e sintetizzare segnali come suoni, immagini, ecc. SciPy fornisce alcune funzioni con cui è possibile progettare, filtrare e interpolare dati monodimensionali e bidimensionali.
Filtraggio:
Filtrare un segnale significa fondamentalmente rimuoverne i componenti indesiderati. Per eseguire un filtraggio ordinato, potete usare la funzione order_filter. Questa funzione fondamentalmente esegue un filtraggio ordinato su un array. La sintassi di questa funzione è la seguente:
SYNTAX:
order_filter(a, domain, rank)
a = array N-dimensionale di input
domain = array di maschere avente lo stesso numero di dimensioni di `a`
rank = numero non negativo che seleziona gli elementi dalla lista dopo che è stata ordinata (0 è il più piccolo seguito da 1…)
EXAMPLE:
from scipy import signal
x = np.arange(35).reshape(7, 5)
domain = np.identity(3)
print(x,end='nn')
print(signal.order_filter(x, domain, 1))
OUTPUT:
]
]
Waveforms:
Il sottopacchetto scipy.signal consiste anche di varie funzioni che possono essere usate per generare forme d’onda. Una di queste funzioni è chirp. Questa funzione è un generatore di coseni a frequenza variabile e la sintassi è la seguente:
SYNTAX:
chirp(t, f0, t1, f1, method=’linear’, phi=0, vertex_zero=True)
where,

from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()
OUTPUT:

Algebra lineare:
L’algebra lineare si occupa di equazioni lineari e delle loro rappresentazioni usando spazi vettoriali e matrici. SciPy è costruito sulle librerie ATLAS LAPACK e BLAS ed è estremamente veloce nel risolvere problemi relativi all’algebra lineare. Oltre a tutte le funzioni di numpy.linalg, scipy.linalg fornisce anche un certo numero di altre funzioni avanzate. Inoltre, se numpy.linalg non è usato insieme al supporto ATLAS LAPACK e BLAS, scipy.linalg è più veloce di numpy.linalg.
Cercare l’inverso di una matrice:
Matematicamente, l’inverso di una matrice A è la matrice tale che dove è la matrice identità composta da uno lungo la diagonale principale indicata come B=A-1. In SciPy, questo inverso può essere ottenuto usando il metodo linalg.inv.
EXAMPLE:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)
OUTPUT:
]
Finding the Determinants:
Il valore derivato aritmeticamente dai coefficienti della matrice è conosciuto come il determinante di una matrice quadrata. In SciPy, questo può essere fatto usando una funzione det che ha la seguente sintassi:
SYNTAX:
det(a, overwrite_a=False, check_finite=True)
dove,
a : (M, M) è una matrice quadrata
overwrite_a( bool, opzionale) : permette di sovrascrivere i dati in a
check_finite ( bool, opzionale): Per controllare se la matrice di input consiste solo di numeri finiti
ESEMPIO:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)
OUTPUT: -5.0
Eigenvalori sparsi:
Gli autovalori sono un insieme specifico di scalari legati a equazioni lineari. ARPACK fornisce che permettono di trovare gli autovalori (autovettori) abbastanza velocemente. La funzionalità completa di ARPACK è racchiusa in due interfacce di alto livello che sono scipy.sparse.linalg.eigs e scipy.sparse.linalg.eigsh. eigs. L’interfaccia eigs permette di trovare gli autovalori di matrici quadrate reali o complesse non simmetriche, mentre l’interfaccia eigsh contiene interfacce per matrici reali-simmetriche o complesse-ermitiane.
La funzione eigh risolve un problema generalizzato di autovalori per una matrice ermitiana complessa o reale simmetrica.
EXAMPLE:
from scipy.linalg import eigh
import numpy as np
A = np.array(, , , ])
a, b = eigh(A)
print("Selected eigenvalues :", a)
print("Complex ndarray :", b)
OUTPUT:
Gli autovalori selezionati :
Complex ndarray :
]
Strutture di dati spaziali e algoritmi:
I dati spaziali consistono fondamentalmente in oggetti costituiti da linee, punti, superfici, ecc. Il pacchetto scipy.spatial di SciPy può calcolare diagrammi di Voronoi, triangolazioni, ecc. usando la libreria Qhull. Consiste anche di implementazioni KDTree per le interrogazioni dei punti più vicini.
Triangolazioni di Delaunay:
Matematicamente, le triangolazioni di Delaunay per un insieme di punti discreti in un piano è una triangolazione tale che nessun punto nell’insieme dato di punti è all’interno della circonferenza di qualsiasi triangolo.
ESEMPIO:
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()
OUTPUT:

Funzioni di elaborazione delle immagini multidimensionali:
L’elaborazione delle immagini si occupa fondamentalmente di eseguire operazioni su un’immagine per recuperare informazioni o per ottenere un’immagine migliorata da quella originale. Il pacchetto scipy.ndimage consiste in una serie di funzioni di elaborazione e analisi delle immagini progettate per lavorare con array di dimensioni arbitrarie.
Convoluzione e correlazione:
SciPy fornisce una serie di funzioni che permettono la correlazione e la convoluzione di immagini.
- La funzione correlate1d può essere usata per calcolare la correlazione unidimensionale lungo un dato asse
- La funzione correlate permette la correlazione multidimensionale di qualsiasi matrice data con il kernel specificato
- La funzione convolve1d può essere usata per calcolare unadimensionale lungo un dato asse
- La funzione convolve permette la convoluzione multidimensionale di una qualsiasi matrice con il kernel specificato
ESEMPIO:
import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)
OUTPUT: array()
File IO:
Il pacchetto scipy.io fornisce una serie di funzioni che aiutano a gestire file di diversi formati come file MATLAB, file IDL, file Matrix Market, ecc.
Per fare uso di questo pacchetto, è necessario importarlo come segue:
import scipy.io as sio
Per informazioni complete sul sottopacchetto, è possibile consultare il documento ufficiale su File IO.
Ci porta alla fine di questo Tutorial SciPy. Spero che abbiate capito tutto chiaramente. Assicurati di fare pratica il più possibile.
Se vuoi controllare altri articoli sulle tecnologie più di tendenza del mercato come Intelligenza Artificiale, DevOps, Ethical Hacking, allora puoi fare riferimento al sito ufficiale di Edureka.
Fai attenzione ad altri articoli in questa serie che spiegheranno i vari altri aspetti di Python e Data Science.
1. Classificatore di apprendimento automatico in Python
2. Python Scikit-Learn Cheat Sheet
3. Strumenti di apprendimento automatico
4. Librerie Python per scienza dei dati e apprendimento automatico
5. Chatbot in Python
6. Collezioni Python
7. Moduli Python
8. Abilità dello sviluppatore Python
9. Domande e risposte per le interviste OOPs
10. Curriculum per uno sviluppatore Python
11. Analisi esplorativa dei dati in Python
12. Gioco del serpente con il modulo Turtle di Python
13. Stipendio dello sviluppatore Python
14. Analisi delle componenti principali
15. Python vs C++
16. Tutorial Scrapy
17. Web Scraping con Python
18. Metodo di regressione ai minimi quadrati
19. Jupyter Notebook Cheat Sheet
20. Fondamenti di Python
21. Programmi Pattern Python
22. Generatori in Python
23. Decoratore Python
24. Python Spyder IDE
25. Applicazioni mobili usando Kivy in Python
26. I 10 migliori libri per imparare &praticare Python
27. Quadro robotico con Python
28. Gioco del serpente in Python usando PyGame
29. Domande e risposte su Django
30. Top 10 Applicazioni Python
31. Tabelle Hash e Hashmap in Python
32. Python 3.8
33. Macchina a vettori di supporto
34. Tutorial Python