
Le reti neurali e la matematica sono inseparabili ed è probabilmente questo che spaventa la maggior parte delle persone. Ho sentito troppi commenti dubbiosi sul Deep Learning: “Oh, questa è troppa matematica per me da comprendere”, “Quante aziende usano davvero il Deep Learning? Preferisco risparmiarmi lo scervellamento e stare lontano da questi concetti impegnativi”.
Ma se ci pensate, non è così difficile. Fidatevi di me! Per capire perché un algoritmo si comporta in un certo modo, è essenziale comprendere cosa succede dietro le quinte. Complessi algoritmi di apprendimento automatico sono confezionati comodamente per noi oggi e sono solo una chiamata di funzione. Le derivate delle funzioni di attivazione sono concetti un po’ meno ovvi che spesso tendiamo ad ignorare. Tuttavia, formano la base di potenti algoritmi e fare un piccolo sforzo in più per capirli ripaga sicuramente. Dopo aver letto questo articolo sarete un passo più vicini a svelare cosa si nasconde sotto la facciata della “scatola nera”.
Sfondo
Le reti neurali usano una varietà di funzioni di attivazione negli strati nascosti e di uscita per catalizzare il processo di apprendimento. Alcune funzioni di attivazione comunemente usate includono le funzioni Sigmoide e tanH. La funzione di attivazione più popolare è ReLU (Rectified Linear Unit) a causa della sua capacità di superare efficacemente il problema del gradiente che svanisce. Un approfondimento sulle funzioni di attivazione è per un altro giorno. Oggi ci concentreremo sulla matematica dietro la derivata della funzione Sigmoide.
Perché è importante la derivata di una funzione di attivazione?
Come probabilmente sapete, due passi guidano le reti neurali:
- Propagazione in avanti – I dati di input scorrono attraverso la rete e otteniamo l’output previsto. Lo confrontiamo con l’output reale e calcoliamo l’errore.
- Back Propagation – L’errore calcolato è usato per aggiornare i parametri della rete neurale usando la derivata della funzione di attivazione.
La funzione sigmoidea
La funzione sigmoide, caratterizzata da una curva a forma di S, è spesso indicata come un caso speciale della funzione logistica. È più utile nei casi in cui dobbiamo prevedere la probabilità come output.
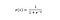
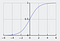
La funzione sigmoide produce valori che stanno tra 0 e 1 (giustamente considerando che predice le probabilità).
La derivata sigmoidea
Questo elemento fondamentale che aiuta ad addestrare le reti neurali assume la forma:


Senza ulteriori indugi, diamoci da fare con la derivazione!
Approccio 1

Approccio 2:
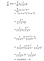
Perché usiamo questa versione del derivato?
Nel passo di propagazione in avanti, si calcola la funzione sigmoide (σ(x)) e si ha il suo valore a portata di mano. Mentre calcolate la derivata nel passo di backpropagation, tutto quello che dovete fare è inserire il valore di σ(x) nella formula derivata sopra e voilà, siete a posto!
Questo è tutto ragazzi! Grazie per aver letto!