Formule Pi

Posted on by admin
Teoria dei Numeri > Costanti > Pi >
Calcolo e Analisi > Serie > Formule BBP >
Calcolo e Analisi > Calcolo > Calcolo > Integrali > Integrali Definiti >
MathWorld Integrali > Integrali definiti >
MathWorld Collaboratori > Cloitre >
MathWorld Collaboratori > Plouffe >
MathWorld Collaboratori > Sondow >

Meno…

Scaricare il Quaderno di Mathematica

Ci sono molte formule di pi di molti tipi. Tra le altre, queste includono serie, prodotti, costruzioni geometriche, limiti, valori speciali e iterazioni di pi greco.

pi è intimamente legato alle proprietà di cerchi e sfere. Per un cerchio di raggio r, la circonferenza e l’area sono date da

C = 2pir
(1)
A = pir^2.
(2)

Similmente, per una sfera di raggio r, la superficie e il volume racchiusi sono

S = 4pir^2
(3)
V = 4/3pir^3.
(4)

Una formula esatta per pi in termini di tangenti inverse di frazioni unitarie è la formula di Machin

1/4pi=4tan^(-1)(1/5)-tan^(-1)(1/(239)).
(5)

Ci sono altre tre formule simili a Machin, così come migliaia di altre formule simili con più termini.

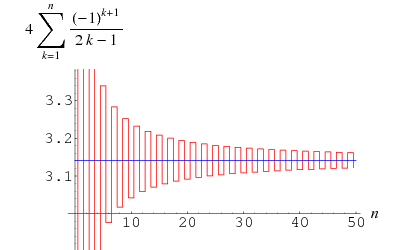
GregorySeries

Gregory e Leibniz trovarono

pi/4 = somma_(k=1)^(infty)((-1)^(k+1))/(2k-1)
(6)
= 1-1/3+1/5-...
(7)

(Wells 1986, p. 50), che è nota come serie di Gregory e può essere ottenuta inserendo x=1 nella serie di Leibniz per tan^(-1)x. L’errore dopo il ntermine di questa serie nella serie di Gregory è più grande di (2n)^(-1) quindi questa somma converge così lentamente che 300 termini non sono sufficienti per calcolare pi correttamente con due cifre decimali! Tuttavia, può essere trasformato in

pi=somma_(k=1)^infty(3^k-1)/(4^k)zeta(k+1),
(8)

dove zeta(z) è la funzione zeta di Riemann (Vardi 1991, pp. 157-158; Flajolet e Vardi 1996), così che l’errore dopo k termini è circa (3/4)^k.

Una serie a somma infinita di Abraham Sharp (ca. 1717) è data da

pi=somma_(k=0)^infty(2(-1)^k3^(1/2-k))/(2k+1)
(9)

(Smith 1953, p. 311). Altre serie semplici in cui compare pi sono

1/4pisqrt(2) = somma_(k=1)^(infty)
(10)
= 1+1/3-1/5-1/7+1/9+1/(11)-...
(11)
1/4(pi-3) = somma_(k=1)^(infty)((-1)^(k+1))/(2k(2k+1)(2k+2))
(12)
= 1/(2-3-4)-1/(4-5-6)+1/(6-7-8)-...
(13)
1/6pi^2 = somma_(k=1)^(infty)1/(k^2)
(14)
= 1+1/4+1/9+1/(16)+1/(25)+...
(15)
1/8pi^2 = somma_(k=1)^(infty)1/((2k-1)^2)
(16)
= 1+1/(3^2)+1/(5^2)+1/(7^2)+...
(17)

(Wells 1986, p. 53).

Nel 1666, Newton usò una costruzione geometrica per ricavare la formula

pi = 3/4sqrt(3)+24int_0^(1/4)sqrt(x-x^2)dx
(18)
= (3sqrt(3))/4+24(1/(12)-1/(5-2^5)-1/(28-2^7)-1/(72-2^9)-...),
(19)

che ha usato per calcolare pi (Wells 1986, p. 50; Borwein et al. 1989; Borwein e Bailey 2003, pp. 105-106). I coefficienti possono essere trovati dall’integrale

I(x) = intsqrt(x-x^2)dx
(20)
= 1/4(2x-1)sqrt(x-x^2)-1/8sin^(-1)(1-2x)
(21)

prendendo l’espansione in serie di I(x)-I(0) intorno a 0, obtaining

I(x)=2/3x^(3/2)-1/5x^(5/2)-1/(28)x^(7/2)-1/(72)x^(9/2)-5/(704)x^(11/2)+...
(22)

(OEIS A054387 e A054388). Usando la trasformazione di miglioramento della convergenza di Eulero dà

pi/2 = 1/2somma_(n=0)^(infty)((n!)^22^(n+1))/((2n+1)!)=somma_(n=0)^(infty)(n!)/((2n+1)!)
(23)
= 1+1/3+(1-2)/(3-5)+(1-2-3)/(3-5-7)+...
(24)
= 1+1/3(1+2/5(1+3/7(1+4/9(1+...))))
(25)

(Beeler et al. 1972, voce 120).

Questo corrisponde a inserire x=1/sqrt(2) nella serie delle potenze della funzione ipergeometrica _2F_1(a,b;c;x),

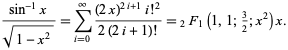(sin^(-1)x)/(sqrt(1-x^2))=sum_(i=0)^infty((2x)^(2i+1)i!^2)/(2(2i+1)!)=_2F_1(1,1;3/2;x^2)x.
(26)

Nonostante il miglioramento della convergenza, la serie (◇) converge ad un solo bit/terma. A costo di una radice quadrata, Gosper ha notato che x=1/2 dà 2 bit/terma,

1/9sqrt(3)pi=1/2sum_(i=0)^infty((i!)^2)/((2i+1)!),
(27)

e x=sin(pi/10) dà quasi 3.39 bit/terma,

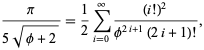pi/(5sqrt(phi+2))=1/2sum_(i=0)^infty((i!)^2)/(phi^(2i+1)(2i+1)!),
(28)

dove phi è il rapporto aureo. Gosper ottenne anche

pi=3+1/(60)(8+(2-3)/(7-8-3)(13+(3-5)/(10-11-3)(18+(4-7)/(13-14-3)(23+...)))).
(29)

Un algoritmo spigot per pi è dato da Rabinowitz e Wagon (1995; Borwein e Bailey 2003, pp. 141-142).

Più sorprendentemente ancora, un’espressione in forma chiusa che dà un algoritmo di estrazione delle cifre che produce cifre di pi (o pi^2) in base-16 è stata scoperta da Bailey et al. (Bailey et al. 1997, Adamchik e Wagon 1997),

pi=somma_(n=0)^infty(4/(8n+1)-2/(8n+4)-1/(8n+5)-1/(8n+6))(1/(16))^n.
(30)

Questa formula, nota come formula BBP, è stata scoperta usando l’algoritmo PSLQ (Ferguson et al. 1999) ed è equivalente a

pi=int_0^1(16y-16)/(y^4-2y^3+4y-4)dy.
(31)

C’è una serie di formule di tipo BBP per pi in potenze di (-1)^k, le cui prime formule indipendenti sono

pi = 4sum_(k=0)^(infty)((-1)^k)/(2k+1)
(32)
= 3sum_(k=0)^(infty)(-1)^k
(33)
= 4sum_(k=0)^(infty)(-1)^k
(34)
= somma_(k=0)^(infty)(-1)^k
(35)
= somma_(k=0)^(infty)(-1)^k
(36)
= somma_(k=0)^(infty)(-1)^k.
(37)

Similmente, esiste una serie di formule di tipo BBP per pi in potenze di 2^k, le cui prime formule indipendenti sono

pi = somma_(k=0)^(infty)1/(16^k)
(38)
= 1/2sum_(k=0)^(infty)1/(16^k)
(39)
= 1/(16)sum_(k=0)^(infty)1/(256^k)
(40)
= 1/(32)sum_(k=0)^(infty)1/(256^k)
(41)
= 1/(32)somma_(k=0)^(infty)1/(4096^k)
(42)
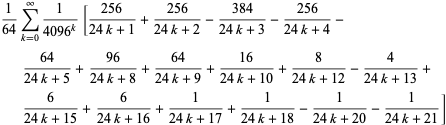= 1/(64)sum_(k=0)^(infty)1/(4096^k)
(43)
= 1/(96)somma_(k=0)^(infty)1/(4096^k)
(44)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(45)
= 1/(96)somma_(k=0)^(infty)1/(4096^k)
(46)
= 1/(4096)sum_(k=0)^(infty)1/(65536^k)
(47)
= 1/(4096)sum_(k=0)^(infty)1/(65536^k).
(48)

F. Bellard ha trovato la formula BBP-type rapidamente convergente

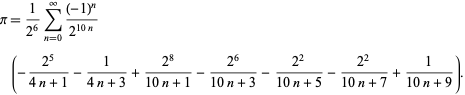pi=1/(2^6)sum_(n=0)^infty((-1)^n)/(2^(10n))(-(2^5)/(4n+1)-1/(4n+3)+(2^8)/(10n+1)-(2^6)/(10n+3)-(2^2)/(10n+5)-(2^2)/(10n+7)+1/(10n+9)).
(49)

Un integrale relativo è

pi=(22)/7-int_0^1(x^4(1-x)^4)/(1+x^2)dx
(50)

(Dalzell 1944, 1971; Le Lionnais 1983, p. 22; Borwein, Bailey, e Girgensohn 2004, p. 3; Boros e Moll 2004, p. 125; Lucas 2005; Borwein et al. 2007, p. 14). Questo integrale era conosciuto da K. Mahler a metà degli anni ’60 e appare in un esame all’Università di Sydney nel novembre 1960 (Borwein, Bailey e Girgensohn, p. 3). Beukers (2000) e Boros e Moll (2004, p. 126) affermano che non è chiaro se esista una scelta naturale di polinomi razionali il cui integrale tra 0 e 1 produce pi-333/106, dove 333/106 è il prossimo convergente. Tuttavia, esiste un integrale per il quarto convergente, cioè

pi=(355)/(113)-1/(3164)int_0^1(x^8(1-x)^8(25+816x^2))/(1+x^2)dx.
(51)

(Lucas 2005; Bailey et al. 2007, p. 219). In effetti, Lucas (2005) fornisce alcuni altri integrali di questo tipo.

Backhouse (1995) ha usato l’identità

I_(m,n) = int_0^1(x^m(1-x)^n)/(1+x^2)dx
(52)
= 2^(-(m+n+1))sqrt(pi)Gamma(m+1)Gamma(n+1)×_3F_2(1,(m+1)/2,(m+2)/2;(m+n+2)/2,(m+n+3)/2;-1)
(53)
= a+bpi+cln2
(54)

per intero positivo m e n e dove a, b, e c sono costanti razionali per generare un certo numero di formule per pi. In particolare, se 2m-n=0 (mod 4), allora c=0 (Lucas 2005).

Una formula simile fu scoperta successivamente da Ferguson, portando ad un reticolo bidimensionale di tali formule che può essere generato da queste due formule date da

pi=sum_(k=0)^infty((4+8r)/(8k+1)-(8r)/(8k+2)-(4r)/(8k+3)-(2+8r)/(8k+4)-(1+2r)/(8k+5)-(1+2r)/(8k+6)+r/(8k+7))(1/(16))^k
(55)

per qualsiasi valore complesso di r (Adamchik e Wagon), dando la formula BBP come caso speciale r=0.

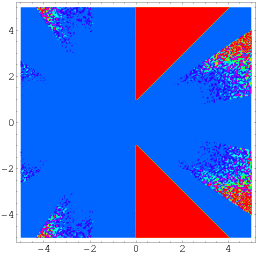
PiFormulasWagonIdentity

Un’identità ancora più generale dovuta a Wagon è data da

pi+4tan^(-1)z+2ln((1-2z-z^2)/(z^2+1))=sum_(k=0)^infty1/(16^k)
(56)

(Borwein e Bailey 2003, p. 141), che vale su una regione del piano complesso che esclude due porzioni triangolari poste simmetricamente intorno all’asse reale, come illustrato sopra.

Una classe di identità forse ancora più strana è data da

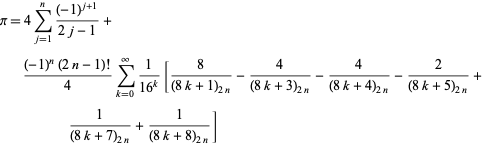pi=4sum_(j=1)^n((-1)^(j+1))/(2j-1)+((-1)^n(2n-1)!)/4sum_(k=0)^infty1/(16^k)
(57)

che vale per qualsiasi intero positivo n, dove (x)_n è un simbolo Pochhammer (B. Cloitre, pers. comm, 23 gennaio 2005). Ancora più sorprendentemente, c’è una formula strettamente analoga per il logaritmo naturale di 2.

Dopo la scoperta della formula BBP in base 16 e delle formule correlate, sono state studiate formule simili in altre basi. Borwein, Bailey e Girgensohn (2004) hanno recentemente dimostrato che pi non ha una formula arctangente BBP di tipo Machin che non sia binaria, anche se questo non esclude uno schema completamente diverso per algoritmi di estrazione delle cifre in altre basi.

S. Plouffe ha ideato un algoritmo per calcolare la nsima cifra di pi in qualsiasi base in O(n^3(logn)^3) passi.

Una serie di identità aggiuntive dovute a Ramanujan, Catalan, e Newton sono date da Castellanos (1988ab, pp. 86-88), incluse diverse che coinvolgono somme di numeri di Fibonacci. Ramanujan ha trovato

sum_(k=0)^infty((-1)^k(4k+1)^3)/(^3)=sum_(k=0)^infty((-1)^k(4k+1)^3)/(pi^(3/2)^3)=2/pi
(58)

(Hardy 1923, 1924, 1999, p. 7).

Plouffe (2006) ha trovato la bella formula

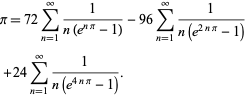pi=72somma_(n=1)^infty1/(n(e^(npi)-1))-96somma_(n=1)^infty1/(n(e^(2npi)-1)) +24somma_(n=1)^infty1/(n(e^(4npi)-1)).
(59)

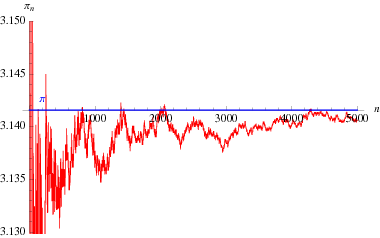
PiBlatnerProduct

Un’interessante formula di prodotto infinito dovuta a Eulero che mette in relazione pi e il nsimo primo p_n è

pi = 2/(prodotto_(n=1)^(infty))
(60)
= 2/(prodotto_(n=2)^(infty))
(61)

(Blatner 1997, p. 119), tracciato sopra come funzione del numero di termini nel prodotto.

Un metodo simile a quello di Archimede può essere usato per stimare pi iniziando con un ngon e poi mettendo in relazione l’area dei successivi 2n-gon. Sia beta l’angolo dal centro di uno dei segmenti del poligono,

beta=1/4(n-3)pi,
(62)

allora

pi=(2sin(2beta))/((n-3)prodotto_(k=0)^(infty)cos(2^(-k)beta))
(63)

(Beckmann 1989, pp. 92-94).

Vieta (1593) fu il primo a dare un’espressione esatta per pi prendendo n=4 nella precedente espressione, dando

cosbeta=sinbeta=1/(sqrt(2))=1/2sqrt(2),
(64)

che porta a un prodotto infinito di radicali annidati,

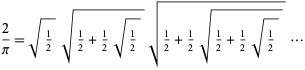2/pi=sqrt(1/2)sqrt(1/2+1/2sqrt(1/2))sqrt(1/2+1/2sqrt(1/2+1/2sqrt(1/2))...
(65)

(Wells 1986, p. 50; Beckmann 1989, p. 95). Tuttavia, questa espressione non fu rigorosamente dimostrata convergente fino a Rudio nel 1892.

Una formula correlata è data da

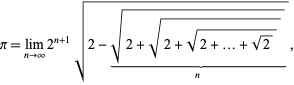pi=lim_(n-infty)2^(n+1)sqrt(2-sqrt(2+sqrt(2+sqrt(2+...+sqrt(2))))_()_(n)),
(66)

che può essere scritto

pi=lim_(n-infty)2^(n+1)pi_n,
(67)

dove pi_n è definito usando l’iterazione

pi_n=sqrt((1/2pi_(n-1))^2+^2)
(68)

con pi_0=sqrt(2) (J. Munkhammar, pers. comm, 27 aprile 2000). La formula

pi=2lim_(m-infty)sum_(n=1)^msqrt(^2+1/(m^2))
(69)

è anche strettamente correlato.

Una bella formula per pi è data da

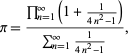pi=(prodotto_(n=1)^(infty)(1+1/(4n^2-1)))/(somma_(n=1)^(infty)1/(4n^2-1)),
(70)

dove il numeratore è una forma della formula di Wallis per pi/2 e il denominatore è una somma telescopica con somma 1/2 poiché

1/(4n^2-1)=1/2(1/(2n-1)-1/(2n+1))
(71)

(Sondow 1997).

Un caso particolare della formula di Wallis dà

pi/2=prodotto_(n=1)^infty=(2-2)/(1-3)(4-4)/(3-5)(6-6)/(5-7)...
(72)

(Wells 1986, p. 50). Questa formula può anche essere scritta

lim_(n-infty)(2^(4n))/(n(2n; n)^2)=pilim_(n-infty)(n^2)/(^2)=pi,
(73)

dove (n; k) denota un coefficiente binomiale e Gamma(x) è la funzione gamma (Knopp 1990). Euler ottenne

pi=sqrt(6(1+1/(2^2)+1/(3^2)+1/(4^2)+...)),
(74)

che segue dal valore speciale della funzione zeta di Riemann zeta(2)=pi^2/6. Formule simili seguono da zeta(2n)per tutti gli interi positivi n.

Una somma infinita dovuta a Ramanujan è

1/pi=somma_(n=0)^infty(2n; n)^3(42n+5)/(2^(12n+4))
(75)

(Borwein et al. 1989; Borwein e Bailey 2003, p. 109; Bailey et al.2007, p. 44). Altre somme sono date in Ramanujan (1913-14),

4/pi=sum_(n=0)^infty((-1)^n(1123+21460n)(2n-1)!!(4n-1)!!)/(882^(2n+1)32^n(n!)^3)
(76)

e

1/pi = sqrt(8)sum_(n=0)^(infty)((1103+26390n)(2n-1)!!(4n-1)!!)/(99^(4n+2)32^n(n!)^3)
(77)
= (sqrt(8))/(9801)sum_(n=0)^(infty)((4n)!(1103+26390n))/((n!)^4396^(4n))
(78)

(Beeler et al. 1972, voce 139; Borwein et al. 1989; Borwein e Bailey 2003, p. 108; Bailey et al. 2007, p. 44). L’equazione (78) deriva da un’identità modulare di ordine 58, sebbene una prima derivazione non sia stata presentata prima di Borwein e Borwein (1987). Le serie precedenti danno entrambe

pi circa (9801)/(2206sqrt(2))=3.14159273001...
(79)

(Wells 1986, p. 54) come prima approssimazione e forniscono, rispettivamente, circa 6 e 8 cifre decimali per termine. Tali serie esistono a causa della razionalità di vari invarianti modulari.

La forma generale della serie è

sum_(n=0)^infty((6n)!)/((3n)!(n!)^3)1/(^n)=(sqrt(-j(t)))/pi,
(80)

dove t è un discriminante binario della forma quadratica, j(t) è la funzione j,

b(t) = sqrt(t)
(81)
a(t) = (b(t))/6{1-(E_4(t))/(E_6(t))},
(82)

e le E_i sono serie di Eisenstein. Un campo di numero di classe p coinvolge pinteri algebrici di terzo grado delle costanti A=a(t), B=b(t), e C=c(t). Di tutte le serie composte da soli termini interi, quella che dà il maggior numero di cifre numeriche nel più breve periodo di tempo corrisponde al più grande discriminante di classe numero 1 d=-163 ed è stata formulata dai fratelli Chudnovsky (1987). Il 163 che appare qui è lo stesso che appare nel fatto che e^(pisqrt(163)) (la costante di Ramanujan) è quasi un intero. Allo stesso modo, il fattore 640320^3 viene dall’identità della funzione j per j(1/2(1+isqrt(163)) . La serie è data da

1/pi = 12sum_(n=0)^(infty)((-1)^n(6n)!(13591409+545140134n))/((n!)^3(3n)!(640320^3)^(n+1/2))
(83)
= (163·8·27·7·11·19·127)/(640320^(3/2))sum_(n=0)^(infty)((13591409)/(163·2·9·7·11·19·127)+n)((6n)!)/((3n)!(n!)^3)((-1)^n)/(640320^(3n))
(84)

(Borwein e Borwein 1993; Beck e Trott; Bailey et al. 2007, p. 44). Questa serie dà accuratamente 14 cifre per termine. La stessa equazione in un’altra forma è stata data dai fratelli Chudnovsky (1987) ed è usata dal linguaggio Wolfram per calcolare pi (Vardi 1991; Wolfram Research),

pi=(426880sqrt(10005))/(A),
(85)

dove

A = 13591409
(86)
B = -1/(151931373056000)
(87)
C = (30285563)/(1651969144908540723200).
(88)

La formula migliore per la classe numero 2 (discriminante maggiore -427) è

1/pi=12sum_(n=0)^infty((-1)^n(6n)!(A+Bn))/((n!)^3(3n)!C^(n+1/2)),
(89)

dove

A = 212175710912sqrt(61)+1657145277365
(90)
B = 13773980892672sqrt(61)+107578229802750
(91)
C = ^3
(92)

(Borwein e Borwein 1993). Questa serie aggiunge circa 25 cifre per ogni termine aggiuntivo. La serie convergente più veloce per la classe numero 3 corrisponde a d=-907 e dà 37-38 cifre per termine. La serie convergente più veloce per la classe numero 4 corrisponde a d=-1555 ed è

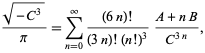(sqrt(-C^3))/pi=somma_(n=0)^infty((6n)!)/((3n)!(n!)^3)(A+nB)/(C^(3n)),
(93)

dove

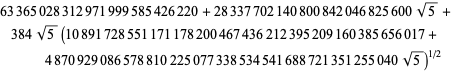A = 63365028312971999585426220+28337702140800842046825600sqrt(5)+384sqrt(5)(10891728551171178200467436212395209160385656017+4870929086578810225077338534541688721351255040sqrt(5))^(1/2)
(94)
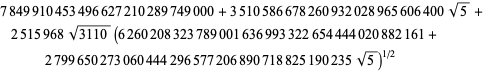B = 7849910453496627210289749000+3510586678260932028965606400sqrt(5)+2515968sqrt(3110)(6260208323789001636993322654444020882161+2799650273060444296577206890718825190235sqrt(5))^(1/2)
(95)
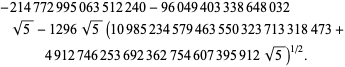C = -214772995063512240-96049403338648032sqrt(5)-1296sqrt(5)(10985234579463550323713318473+4912746253692362754607395912sqrt(5))^(1/2).
(96)

Questo dà 50 cifre per termine. Borwein e Borwein (1993) hanno sviluppato un algoritmo generale per generare tali serie per un numero di classe arbitrario.

Un elenco completo delle serie di Ramanujan per 1/pi trovate nel suo secondo e terzo quaderno è dato da Berndt (1994, pp. 352-354),

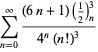4/pi = somma_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!)^3)
(97)
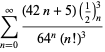(16)/pi = somma_(n=0)^(infty)((42n+5)(1/2)_n^3)/(64^n(n!)^3)
(98)
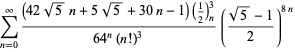(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(99)
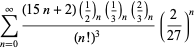(27)/(4pi) = sum_(n=0)^(infty)((15n+2)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(2/(27))^n
(100)
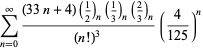(15sqrt(3))/(2pi) = sum_(n=0)^(infty)((33n+4)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(4/(125))^n
(101)
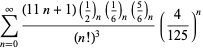(5sqrt(5))/(2pisqrt(3)) = sum_(n=0)^(infty)((11n+1)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(125))^n
(102)
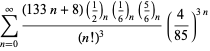(85sqrt(85))/(18pisqrt(3)) = sum_(n=0)^(infty)((133n+8)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(85))^(3n)
(103)
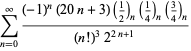4/pi = sum_(n=0)^(infty)((-1)^n(20n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^32^(2n+1))
(104)
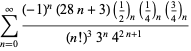4/(pisqrt(3)) = sum_(n=0)^(infty)((-1)^n(28n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^33^n4^(2n+1))
(105)
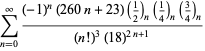4/pi = sum_(n=0)^(infty)((-1)^n(260n+23)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(18)^(2n+1))
(106)
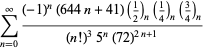4/(pisqrt(5)) = sum_(n=0)^(infty)((-1)^n(644n+41)(1/2)_n(1/4)_n(3/4)_n)/((n!)^35^n(72)^(2n+1))
(107)
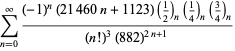4/pi = sum_(n=0)^(infty)((-1)^n(21460n+1123)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(882)^(2n+1))
(108)
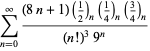(2sqrt(3))/pi = sum_(n=0)^(infty)((8n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^n)
(109)
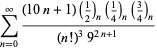1/(2pisqrt(2)) = sum_(n=0)^(infty)((10n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^(2n+1))
(110)
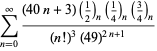1/(3pisqrt(3)) = sum_(n=0)^(infty)((40n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(49)^(2n+1))
(111)
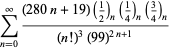2/(pisqrt(11)) = sum_(n=0)^(infty)((280n+19)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(2n+1))
(112)
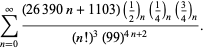1/(2pisqrt(2)) = sum_(n=0)^(infty)((26390n+1103)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(4n+2)).
(113)

Queste equazioni furono dimostrate per la prima volta da Borwein e Borwein (1987a, pp. 177-187). Borwein e Borwein (1987b, 1988, 1993) dimostrarono altre equazioni di questo tipo, e Chudnovsky e Chudnovsky (1987) trovarono equazioni simili per altre costanti trascendentali (Bailey et al. 2007, pp. 44-45).

Un elenco completo di equazioni indipendenti note di questo tipo è dato da

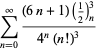4/pi = sum_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!)^3)
(114)
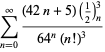(16)/pi = somma_(n=0)^(infty)((42n+5)(1/2)_n^3)/(64^n(n!)^3)
(115)
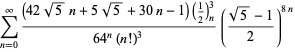(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(116)
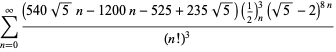(5^(1/4))/pi = sum_(n=0)^(infty)((540sqrt(5)n-1200n-525+235sqrt(5))(1/2)_n^3(sqrt(5)-2)^(8n))/((n!)^3)
(117)
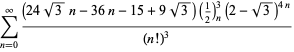(12^(1/4))/pi = somma_(n=0)^(infty)((24sqrt(3)n-36n-15+9sqrt(3))(1/2)_n^3(2-sqrt(3))^(4n))/((n!)^3)
(118)

per m=1 con segni non alternati,

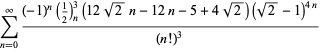2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(12sqrt(2)n-12n-5+4sqrt(2))(sqrt(2)-1)^(4n))/((n!)^3)
(119)
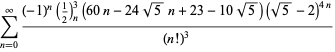2/pi = somma_(n=0)^(infty)((-1)^n(1/2)_n^3(60n-24sqrt(5)n+23-10sqrt(5))(sqrt(5)-2)^(4n))/((n!)^3)
(120)
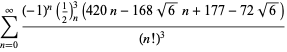2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(420n-168sqrt(6)n+177-72sqrt(6)))/((n!)^3)
(121)
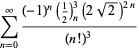(2sqrt(2))/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(2sqrt(2))^(2n))/((n!)^3)
(122)

per m=1 con segni alterni,

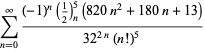(128)/(pi^2) = somma_(n=0)^(infty)((-1)^n(1/2)_n^5(820n^2+180n+13))/(32^(2n)(n!)^5)
(123)
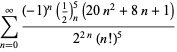(32)/(pi^2) = sum_(n=0)^(infty)((-1)^n(1/2)_n^5(20n^2+8n+1))/(2^(2n)(n!)^5)
(124)

per m=2 (Guillera 2002, 2003, 2006),

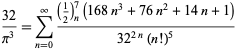(32)/(pi^3)=sum_(n=0)^infty((1/2)_n^7(168n^3+76n^2+14n+1))/(32^(2n)(n!)^5)
(125)

per m=3 (Guillera 2002, 2003, 2006), e non sono noti altri per m3 (Bailey et al. 2007, pp. 45-48).

Bellard dà la formula esotica

pi=1/(740025),
(126)

where

P(n)=-885673181n^5+3125347237n^4-2942969225n^3+1031962795n^2-196882274n+10996648.
(127)

Gasper cita il risultato

pi=(16)/3^(-1),
(128)

dove _1F_2 è una funzione ipergeometrica generalizzata, e la trasforma in

pi=lim_(x-infty)4x_1F_2(1/2;3/2,3/2;-x^2).
(129)

Un risultato affascinante dovuto a Gosper è dato da

lim_(n-infty)prodotto_(i=n)^(2n)pi/(2tan^(-1)i)=4^(1/pi)=1.554682275....
(130)

pi soddisfa la disuguaglianza

(1+1/pi)^(pi+1) circa 3,14097pi.
(131)

D. Terr (pers. comm.) ha notato la curiosa identità

(3,1,4)=(1,5,9)+(2,6,5) (mod 10)
(132)

che coinvolge le prime 9 cifre di pi greco.

Lascia un commento

Il tuo indirizzo email non sarà pubblicato.