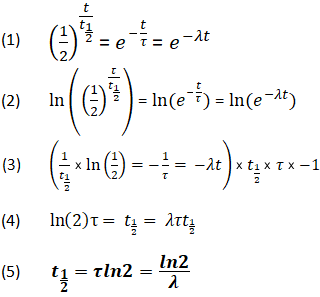I seguenti strumenti possono generare uno qualsiasi dei valori dagli altri tre nella formula dell’emivita per una sostanza in decadimento per diminuire della metà.

Half Life Calculator
Si prega di fornire uno qualsiasi dei tre seguenti per calcolare il quarto valore.
Conversione di Mezza Vita, Vita Media e Costante di Decadimento
Per favore fornisci uno qualsiasi dei seguenti per ottenere gli altri due.
Definizione e Formula
La mezza vita è definita come la quantità di tempo che impiega una data quantità a diminuire alla metà del suo valore iniziale. Il termine è più comunemente usato in relazione agli atomi sottoposti a decadimento radioattivo, ma può essere usato per descrivere altri tipi di decadimento, esponenziale o meno. Una delle applicazioni più note dell’emivita è la datazione al carbonio-14. L’emivita del carbonio-14 è di circa 5.730 anni, e può essere usato in modo affidabile per misurare date fino a circa 50.000 anni fa. Il processo di datazione al carbonio-14 è stato sviluppato da William Libby e si basa sul fatto che il carbonio-14 viene costantemente prodotto nell’atmosfera. Viene incorporato nelle piante attraverso la fotosintesi, e poi negli animali quando consumano le piante. Il carbonio-14 subisce un decadimento radioattivo una volta che la pianta o l’animale muore, e la misurazione della quantità di carbonio-14 in un campione fornisce informazioni su quando la pianta o l’animale sono morti.
Di seguito sono mostrate tre formule equivalenti che descrivono il decadimento esponenziale:
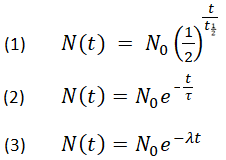
- dove
N0 è la quantità iniziale
Nt è la quantità rimanente dopo il tempo, t
t1/2 è il tempo di dimezzamento
τ è la vita media
λ è la costante di decadimento
Se un archeologo trova un campione fossile che contiene il 25% di carbonio-14 rispetto ad un campione vivente, il tempo della morte del campione fossile potrebbe essere determinato riorganizzando l’equazione 1, poiché Nt, N0 e t1/2 sono noti.
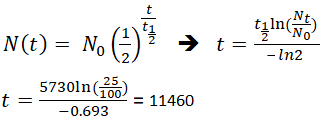
Questo significa che il fossile ha 11.460 anni.
Derivazione della relazione tra le costanti di emivita
Utilizzando le equazioni di cui sopra, è anche possibile derivare una relazione tra t1/2, τ e λ. Questa relazione permette la determinazione di tutti i valori, purché almeno uno sia noto.