Il proporzionale è solo un modo per reagire a un errore nel sistema. Il problema del controllo proporzionale è che non può rilevare le tendenze e regolarle. Questo è il lavoro del controllo integrale.
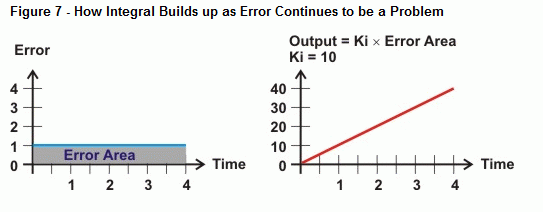
C’è un altro esempio di grafico dell’errore in un sistema nel tempo sulla sinistra della figura 6. Di nuovo, potrebbe essere la distanza di un robot da un oggetto, o potrebbe essere il livello del fluido in un serbatoio, o la temperatura in un forno di fabbrica. Forse l’obiettivo che il robot sta seguendo continua ad allontanarsi dal robot ad una velocità che il robot non riesce a raggiungere. Forse la guarnizione della porta del forno è consumata; forse il prelievo di fluido dal serbatoio è insolitamente grande. Indipendentemente dalla causa, poiché il proporzionale non è progettato per reagire alle tendenze, non può rilevare e correggere il problema. È qui che entra in gioco il controllo integrale.
Integrale misura l’area tra i valori di errore e l’asse del tempo. Se l’errore non torna a zero, l’area dell’errore diventa sempre più grande. Il lato destro della figura 6 mostra come l’uscita integrale può reagire a questo tipo di tendenza. Come l’area tra la curva dell’errore e l’asse del tempo aumenta, l’uscita aumenta proporzionalmente a quest’area. Come risultato, l’uscita spinge l’attuatore sempre più forte per correggere l’errore.
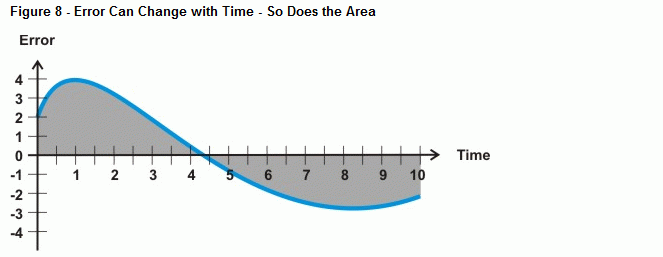
Quindi cosa succede quando l’errore non è una linea retta, come la curva mostrata nella figura 8? Questo è ciò che determina l’operazione di calcolo dell’integrazione, l’area tra una curva e un asse. Nel caso del controllo integrale, man mano che passa più tempo con un errore, l’area sotto la curva cresce, e così il valore che il calcolo integrale userà per contrastare l’errore del sistema. Se la curva di errore scende sotto l’asse del tempo, l’accumulo di area negativa si sottrae all’accumulo di area positiva. Se sintonizzato correttamente, il controllo integrale può aiutare il sistema ad affinare un errore di zero.
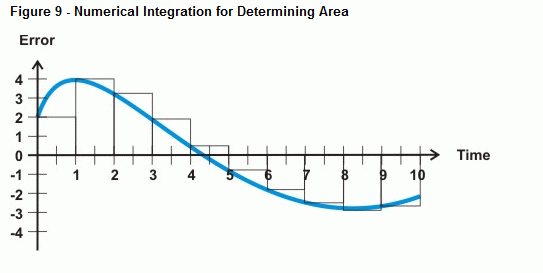
Il BASIC Stamp può approssimare l’errore sotto la curva con l’integrazione numerica. La figura 9 mostra come si può approssimare l’errore sotto una curva sommando l’area di un mucchio di piccoli rettangoli tra la curva di errore e l’asse del tempo. L’area di ogni casella è l’errore moltiplicato per il tempo tra le misurazioni. Sommando tutte le aree delle caselle, si ottiene un’approssimazione dell’area sotto la curva.
Finché le vostre misure sono uniformemente distanziate, potete chiamare la larghezza di ogni casella un valore di 1. Questo rende la matematica molto più semplice che cercare di tenere conto di 20 ms tra i campioni, 5 minuti tra i campioni, o qualunque sia la vostra frequenza di campionamento. Invece di moltiplicare l’errore per l’incremento di tempo tra i campioni e poi aggiungere al prossimo errore moltiplicato per il tempo, potete semplicemente moltiplicare ogni campione di errore per un tempo di 1. Il risultato è che potete semplicemente tenere un totale corrente delle misure di errore per il vostro calcolo integrale. Ecco un esempio di come fare questo con PBASIC:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
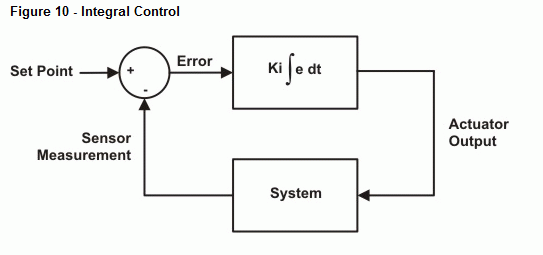
Il prossimo esempio di programma esegue l’integrazione numerica sul segnale di errore e regola l’uscita di conseguenza. Come per il controllo proporzionale, c’è una costante che scala l’uscita di integrazione al valore desiderato. Per semplicità, useremo ancora 10 per Ki. La figura 10 mostra un diagramma a blocchi dell’anello di controllo. Il termine Kp ∫ edt si riferisce a Kp moltiplicato per l’integrale dell’errore nel tempo. In altre parole, Kp moltiplicato per l’area accumulata tra la curva di errore e l’asse del tempo.
Programma di esempio – IntegralAlgorithm.bs2
- Inserisci, salva ed esegui IntegralAlgorithm.bs2.
- Inserisci questa sequenza di valori nel pannello della finestra di trasmissione del terminale di debug: 3 3 3 3 3 3 3 3 3. Notate come l’output dell’integrale diventa più grande ogni volta che il 3 viene ripetuto. Questo è il lavoro dell’integrale, per rilevare le tendenze e aumentare l’unità per correggerle come necessario.
- Ora prova questa sequenza: 1 2 3 4 5 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0. L’area sotto questa curva è 0 poiché l’area negativa è uguale a quella positiva. Questo è anche il risultato del calcolo integrale quando avete finito di inserire la sequenza.
' IntegralAlgorithm.bs2' Demonstrates how integral control influences error correction' in a feedback loop. ' {$STAMP BS2}' {$PBASIC 2.5} SetPoint CON 0 ' Set pointKi CON 10 ' Integral constant Current CON 0 ' Array index for current errorAccumulator CON 1 ' Array index for accumulated error sensorInput VAR Word ' Inputerror VAR Word(2) ' Two element error arrayi VAR Word ' Integral termdrive VAR Word ' Output DO DEBUG "Enter sensor input value: " DEBUGIN SDEC sensorInput ' Calculate error. error(Current) = SetPoint - sensorInput ' Calculate integral term. error(Accumulator) = error(Accumulator) + error(Current) i = Ki * error(Accumulator) ' Calculate output. drive = i ' Display values. DEBUG CR, CR, "ERROR", CR, SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR, "INTEGRAL", CR, SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR, "OUTPUT", CR, SDEC ? i, SDEC ? drive, CR, CR LOOP
Come funziona IntegralAlgorithm.bs2
Questo programma è un ProportionalAlgorithm.bs2 modificato per eseguire invece il calcolo integrale. Ora ci sono due diversi tipi di errori di cui tenere traccia, quindi l’array della variabile error è stato ampliato a due elementi. La variabile error(0) traccia l’errore corrente, ed error(1) traccia l’errore accumulato. Le costanti Current CON 0 e Accumulator CON 1 rendono la contabilità un po’ più sensata con error(current) e error(accumulator).
L’altro cambiamento che è stato fatto è che l’errore è accumulato e l’uscita integrale è calcolata con queste due dichiarazioni:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
Tu tocca – Clamping the Integral Output
Come avrai capito inserendo ripetutamente 3 nel Debug Terminal, l’uscita integrale del drive può davvero iniziare a correre via. Potete usare gli operatori MIN e MAX per evitare che il controllo integrale esageri con l’uscita. Ripetiamo l’attività di offset del servo e limitiamo l’uscita da 650 a 850.
- Cambia l’istruzione drive = i in drive = i + Offset MIN 650 MAX 850.
- Esegui il programma e verifica che l’uscita integrale sia limitata a valori tra 650 e 850. Provate a inserire ripetutamente 2, poi -2 ripetutamente.