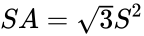Per la rivista accademica, vedi Tetrahedron (rivista).
| Tetraedro regolare | |
|---|---|
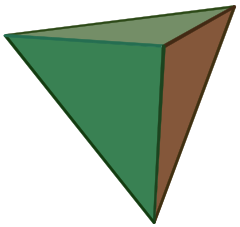 (Clicca qui per il modello rotante) |
|
| Tipo | Solido platonico |
| Elementi | F = 4, E = 6 V = 4 (χ = 2) |
| Facce per lati | 4{3} |
| Schläfli simbolo | {3,3} e s{2,2} |
| Simbolo di Wythoff | 3 | 2 3 | 2 2 2 |
| Coxeter-Dynkin | |
| Simmetria | Td o (*332) |
| U01, C15, W1 | |
| Proprietà | deltaedro convesso regolare |
| Angolo diedro | 70.528779° = arccos(1/3) |
 3.3.3 (figura del vertice) |
 Self-dual (poliedro duale) |
 Net |
|
Un tetraedro (plurale: tetraedri) è un poliedro composto da quattro facce triangolari, tre delle quali si incontrano in ogni vertice. Un tetraedro regolare è quello in cui i quattro triangoli sono regolari, o “equilateri”, ed è uno dei solidi platonici.
Il tetraedro è un tipo di piramide, che è un poliedro con una base poligonale piatta e facce triangolari che collegano la base ad un punto comune. Nel caso di un tetraedro la base è un triangolo (una qualsiasi delle quattro facce può essere considerata la base), quindi un tetraedro è anche conosciuto come piramide triangolare o deltaedro digonale.
Formule per il tetraedro regolare
Il volume è
La superficie è
Template:Commonscat
- F. M. Jackson e Weisstein, Eric W., “Tetrahedron” da MathWorld.
- Weisstein, Eric W., “Tetrahedron” da MathWorld.
- Weisstein, Eric W., “Tetrahedron” da MathWorld.
- I poliedri uniformi
- Tetraedro: Modello poliedrico interattivo
- K. J. M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- La formula di Piero della Francesca per il volume del tetraedro a MathPages
- Modelli di carta gratuiti di un tetraedro e molti altri poliedri
- Un incredibile, Space Filling, Non-regular Tetrahedron che include anche una descrizione di un “anello rotante di tetraedri”, noto anche come un caleidociclo.
- Tetrahedron Core Network Applicazione di una struttura tetraedrica per creare una rete di dati a maglie parziali resistente
- Formule esatte esplicite per il tensore d’inerzia di un tetraedro arbitrario in termini di coordinate dei suoi vertici
- Il tensore d’inerzia di un tetraedro