Introduzione
Le trasformazioni di coordinate sono abbastanza non intuitive in 2-D, e positivamente dolorose in 3-D. Questa pagina le affronta nel seguente ordine: (i) vettori in 2-D, (ii) tensori in 2-D, (iii) vettori in 3-D, (iv) tensori in 3-D, e infine (v) trasformazioni tensoriali di 4° grado.
Un aspetto importante delle trasformazioni di coordinate è la valutazione della matrice di trasformazione, specialmente in 3-D. È molto importante riconoscere che tutte le trasformazioni di coordinate in questa pagina sono rotazioni del sistema di coordinate mentre l’oggetto stesso rimane fisso. L'”oggetto” può essere un vettore come la forza o la velocità, o un tensore come lo stress o la deformazione in un componente. Le rotazioni degli oggetti sono discusse nelle sezioni successive.
Trasformazioni di coordinate 2-D dei vettori
La patata accademica fornisce un eccellente esempio di come le trasformazioni di coordinate si applicano ai vettori, mentre allo stesso tempo sottolinea che è il sistema di coordinate che sta ruotando e non il vettore… o la patata.
La patata sulla sinistra ha un vettore su di essa. Ma senza un sistema di coordinate, non c’è modo di descrivere il vettore.Quindi un sistema di coordinate è stato aggiunto alla patata come mostrato sulla destra, permettendo al vettore di essere descritto come \({\bf v} = 2{\bf i} + 9{\bf j}).

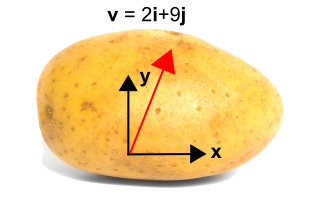
Ora introduciamo un sistema di coordinate ruotato mostrato in blu qui sotto, usando \(x’\) e \(y’\). Il nuovo sistema è ruotato in senso antiorario di un angolo, \(\ilta\), dal sistema di coordinate iniziale. Si noti che il vettore stesso non cambia affatto. È ancora lo stesso vettore di prima. Ma è descritto da valori numerici diversi nel nuovo sistema di coordinate. In questo caso, il vettore è più strettamente parallelo al nuovo asse \(x’\) che all’asse \(y’\), quindi la componente \({\bf i’}}) sarà maggiore della componente \({\bf j’}). La trasformazione è data sotto la figura.
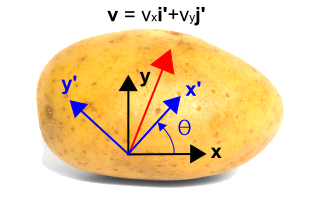
Questo può essere visto notando che Questi quattro fattori costituiscono i quattro termini nelle equazioni di trasformazione. Essi sono facilmente verificabili impostando \(\theta = 0^circa \) e \(\theta = 90^circa \). Quando \(\theta = 0^circ \), allora \(v’_x = v_x\) e \(v’_y = v_y\). Quando \(\theta = 90^circa), allora \(v’_x = v_y\) e \(v’_y = -v_x\).
Matrice di trasformazione
È più conveniente scrivere (e lavorare con) le equazioni di trasformazione usando le matrici.
Sinistra \matrice {v_x \ v_y}
I termini \cos \theta\ sono sulla diagonale della matrice mentre i termini \sin \theta\ sono fuori diagonale. L’unico potenziale intoppo è ricordare quale termine \(\sin \theta\) ha il segno meno. È sempre il termine in basso a sinistra.
L’equazione di cui sopra è scritta in notazione matriciale come
dove \({\bf Q}}) è la solita lettera scelta per la matrice di trasformazione.

Matrici di trasformazione e di rotazione
Se questo argomento non fosse già abbastanza difficile, molti libri e siti web aggiungono confusione non chiarendo cosa è fisso e cosa è rotante. In questa pagina e nella prossima, è il sistema di coordinate che sta ruotando mentre l’oggetto rimane fisso, quindi il termine matrice di trasformazione è usato qui per sottolineare questo.
Tuttavia, affronteremo più tardi situazioni in cui l’oggetto ruota mentre il sistema di coordinate rimane fisso. In questo scenario, il termine matrice di rotazione sarà usato per sottolineare che l’oggetto sta ruotando.
Molta confusione nasce dal fatto sorprendente che ogni matrice (trasformazione e rotazione) è solo la trasposizione dell’altra! Quindi sembrano estremamente simili. Nei problemi 2-D, l’unica differenza pratica è se il segno meno davanti a \(\sin \theta\) è sul termine \(q_{12}) o sul termine \(q_{21}).
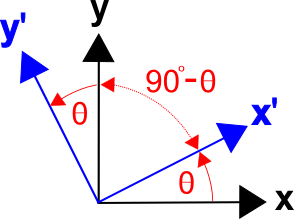
Esiste un metodo generale per formulare matrici di trasformazione basate sui coseni degli angoli tra gli assi dei due sistemi di coordinate, cioè i coseni di direzione. (La matrice di trasformazione può essere scritta come
\\]
dove \((x’,x)\) rappresenta l’angolo tra gli assi \(x’\) e \(x’\), \((x’,y)\) è l’angolo tra gli assi \(x’\) e \(y’\), ecc.
L’angolo tra \(x’\) e \(y’\) è \(90^circa – \theta)\), e \(\cos(x’,y) = \cos(90^circa – \theta) = \sin \theta\).
Parimenti, l’angolo tra \(y’\) e \(x’\) è \((90^\circ + \theta)\), e \(\cos(y’,x) = \cos(90^\circ + \theta) = -\sin \theta\).
Notazione tensoriale
La trasformazione delle coordinate è scritta in notazione tensoriale come
dove \(\lambda_{ij}}) è la matrice di trasformazione \({\bf Q}). (Non so perché si usa \bf Q} in notazione matriciale, ma \(\lambda_{ij}), non \(q_{ij}), è usato in notazione tensoriale). \(\lambda_{ij}) è definito come
\
Per esempio, se \(i = 1\) e \(j = 2\), allora
\
\(\lambda_{ij}) è il coseno della direzione dell’angolo tra l’asse \(x’_i\) e l’asse \(x_j\). Di nuovo, questo è ugualmente applicabile anche alle trasformazioni 3-D.
Trasformazioni di coordinate 2-D dei tensori
Questa sezione presenterà il cosa e il come delle trasformazioni tensoriali.Il perché dovrà aspettare fino a dopo.
Le trasformazioni di coordinate dei tensori di 2° grado coinvolgono la stessa matrice \({\bf Q})delle trasformazioni vettoriali. Una trasformazione del tensore di stress, \(\boldsymbol{sigma}), dal sistema di coordinate di riferimento \(x-y) a \(\boldsymbol{sigma’}) in un nuovo sistema \(x’-y’\) è fatta come segue.
Scrivendo esplicitamente le matrici si ottiene
= \sinistra \sinistra \sinistra \sinistra \]
(Si noti che il tensore di sforzo è sempre simmetrico, anche dopo le trasformazioni.)
Moltiplicando le matrici si ottiene
Queste tre equazioni sono esattamente la trasformazione 2-D di un tensore di sollecitazione che risulta dalla somma delle forze su un elemento differenziale e dall’imposizione dell’equilibrio. Questo è anche rappresentato dal cerchio di Mohr.
Notazione tensoriale
La trasformazione delle coordinate è scritta in notazione tensoriale come
Come al solito, la notazione tensoriale fornisce un’ulteriore comprensione del processo. Questa volta, l’intuizione viene dai pedici sui lambda. Ogni lambda effettivamente accoppia un pedice su \(\boldsymbol{sigma’}) con uno su \(\boldsymbol{sigma’}).Questo è vero indipendentemente dal rango del tensore.
Trasformazioni di coordinate 3-D di vettori
Molte delle equazioni generali usate nelle trasformazioni 2-D sono applicabili anche in 3-D. Gli esempi includono
Solo che ora i dettagli sono diversi. I vettori hanno componenti z e le matrici di trasformazione sono 3×3 invece che 2×2.
]
\matrice sinistra \matrice v_x \ v_y \ v_z }
Trasformazioni di coordinate 3-D di tensori
Ancora una volta, le regole non cambiano, solo i particolari sì.
Scrivendo le matrici esplicitamente si ottiene
\ = \left\left\left\]
Questa pagina web esegue trasformazioni di coordinate su tensori 3-D. Provala.
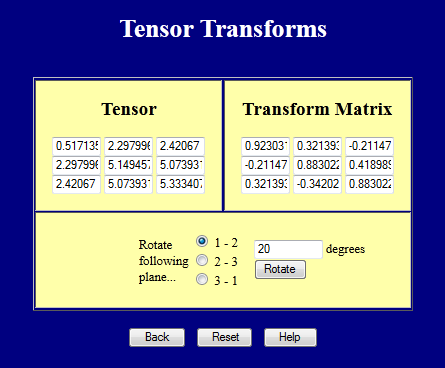
Trasformazioni di coordinate di tensori di 4° rango
Vedremo nella sezione sulla legge di Hooke che il tensore di rigidità è di 4° rango, cioè 3x3x3x3 (non 4×4). Si scrive come C_{ijkl} perché mette in relazione qualsiasi componente di deformazione, \(\epsilon_{kl}), con qualsiasi componente di sforzo, \(\sigma_{ij}), cioè, \La legge di trasformazione delle coordinate per il tensore di rigidità di 4° rango è facilmente scritta in notazione tensoriale come
L’equazione del tensore indica come scrivere la trasformazione in notazione matriciale.
Sommario
La trasformazione delle coordinate di un vettore in notazione matriciale e tensoriale è
La trasformazione delle coordinate di un tensore in notazione matriciale e tensoriale è
Nota che \({\bf Q}\) e \(\lambda_{ij}) sono la stessa matrice di trasformazione.
In 2-D, \({\bf Q}}) e \(\lambda_{ij}) sono definiti come
\\]
che è un caso speciale della più generale forma 3-D
\]