円周率の公式

Posted on by admin
数論 > 定数 > 円周率 >
微積分と解析 > 直列 > BBP 公式 >
微積分と解析 > 計算 > 積分 > 定積分 >
MathWorld Contributors > Cloitre >
MathWorld Contributors > Plouffe >
MathWorld Contributors > Sondow >

以下略です。..
DOWNLOAD Mathematica Notebook

pi の公式は多くの種類があります。 中でも、級数、積、幾何学的構成、極限、特別な値、円周率の反復などがあります。

pi は円や球の性質と密接に関係しています。 半径rの円の場合。 円周と面積は

C = 2pir
(1)
A = pir^2 で表されます。
(2)

同様に、半径rの球の場合です。 表面積と囲まれた体積は

である。

S = 4pir^2
(3)
V = 4/3pir^3.
(4)

単位分数の逆正接でpiの正確な式はMachinの式

1/4pi=4tan^(-1)(1/5)-tan^(-1)(1/(239))ですな。
(5)

Machinに似た公式は他に3つあり、さらに項数が多い類似の公式は何千とあります。

GregorySeries

Gregory と Leibniz は

pi/4 = sum_(k=1)^(infty)((-))1)^(k+1))/(2k-1)
(6)
= 1-1/3+1/5-....
(7)

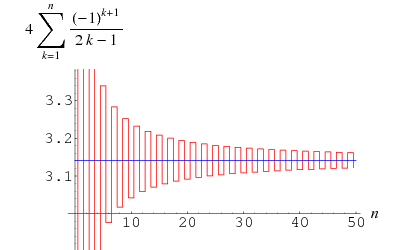
(Wells 1986, p. 50) これはグレゴリー級数と呼ばれ、x=1 を tan^(-1)x の Leibniz シリーズに差し込むことにより求められるかもしれない。 グレゴリー級数のこの級数のn番目の項以降の誤差は(2n)^(-1)より大きいので、この和は収束が遅く、300項ではpiを小数2桁まで正しく計算できない! しかし、

pi=sum_(k=1)^infty(3^k-1)/(4^k)zeta(k+1) に変形することができる。
(8)

ここで zeta(z) はリーマンのゼータ関数（Vardi 1991, pp. 157-158; Flajolet and Vardi 1996）、k項後の誤差は約 (3/4)^k となる。

Abraham Sharp (ca. 1717)への無限和級数は

pi=sum_(k=0)^infty(2(-1)^k3^(1/2-k))/(2k+1)
(9)

(Smith 1953, p. 311) によって与えられます。 さらにpiが現れる単純級数は

であり、piが登場するのは

.

1/4pisqrt(2) = sum_(k=1)^(infty)
(10)
= 1+1/3-1/5-1/7+1/9+1/(11)-...
(11)
1/4(pi-3) = sum_(k=1)^(infty)((-1)^(k+1))/(2k(2k+1)(2k+2))
(12)
= 1/(2-3-4)-1/(4-5-6)+1/(6-7-8)- ですね。..
(13)
1/6π^2 = sum_(k=1)^(infty)1/(k^2)
(14)
= 1+1/4+1/9+1/(16)+1/(25)+...
(15)
1/8π^2 = sum_(k=1)^(infty)1/((2k-))</td> </td></td> <td></td><td><td><td><td><td><td></td> <td width=

(16)
= 1+1/(3^2)+1/(5^2)+1/(7^2)+....
(17)

(Wells 1986, p. 53)となる。

1666年。 ニュートンは幾何学的な構成を使って

pi = 3/4sqrt(3)+24int_0^(1/4)sqrt(x-)</p> を導き出しました。x^2)dx
(18)
= (3sqrt(3))/4+24(1/(12)-1/(5-2^5)-1/(28-2^7)-1/(72-2^9)...-)/)...)、
(19)

を計算し、piを算出した（Wells 1986, p.50; Borwein et al. 1989; Borwein and Bailey 2003, pp.105-106 ）。 係数は積分

I(x) = intsqrt(x-) から求めることができる。x^2)dx
(20)
= 1/4(2x-)1)sqrt(x-x^2)-1/8sin^(-1)(1-2x)
(21)

0 について I(x)-I(0) の系列展開を取ることにより行うことができる。 obtaining

I(x)=2/3x^(3/2)-1/5x^(5/2)-1/(28)x^(7/2)-1/(72)x^(9/2)-5/(704)x^(11/2)+...
(22)

(OEIS A054387、A054388)となりました。 オイラーの収束改善変換を使うと

pi/2 = 1/2sum_(n=0)^(infty)((n!)^22^(n+1))/((2n+1)! )=sum_(n=0)^(infty)(n!)/((2n+1)!) となる。)
(23)
= 1+1/3+(1-2)/(3-5)+(1-2-3)/(3-5-7)+...
(24)
= 1+1/3(1+2/5(1+3/7(1+4/9(1+....))
(25)

(Beeler et al. 1972, Item 120)とある。）

これは超幾何関数 _2F_1(a,b.) の冪級数に <img src= を突っ込むことに相当する。c;x)” class=”alignright”>,

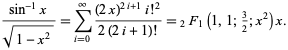(sin^(-1)x)/(sqrt(1-x^2))=sum_(i=0)^infty((2x)^(2i+1)i!^2)/(2(2i+1)!)=_2F_1(1,1;3/2;x^2)x.
(26)

収束性が向上したにもかかわらず、系列(◇)は1ビット/項でしか収束しない。 平方根を犠牲にして、Gosper は x=1/2 が 2 bit/term を与えることに注目している、

1/9sqrt(3)pi=1/2sum_(i=0)^infty((i!)) 1/9sqrt(3)pi=1/2sum_(i=0)^infty(i!)^2)/((2i+1)!),
(27)

そして x=sin(pi/10) でほぼ3が得られます。39 bit/term,

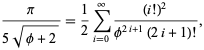pi/(5sqrt(phi+2))=1/2sum_(i=0)^infty((i!)^2)/(phi^(2i+1)(2i+1) !となります。),
(28)

ここで phi は黄金比である。 ゴスパーも

pi=3+1/(60)(8+(2-3)/(7-8-3)(13+(3-5)/(10-11-3)(18+(4-7)/(13-14-3)(23+...))) を求めています。）
(29)

pi に対するスピゴットのアルゴリズムはRabinowitz and Wagon (1995; Borwein and Bailey 2003, pp. 141-142) により与えられています。

さらに驚くべきことに、16進数でpi (またはpi^2)の数字を生成する数字抽出アルゴリズムを与える閉形式がBaileyらによって発見された。 (Bailey et al. 1997, Adamchik and Wagon 1997),

pi=sum_(n=0)^infty(4/(8n+1)-2/(8n+4)-1/(8n+5)-1/(8n+6))(1/(16))^n.
(30)

この式はBBP式と呼ばれ、PSLQアルゴリズム（Ferguson et al. 1999）を用いて発見され、

pi=int_0^1(16y-16)/(y^4-2y^3+4y-4)dy に等価である。
(31)

pi の (-1)^k 乗のBBP型公式のシリーズがある。 最初のいくつかの独立した式は、

pi = 4sum_(k=0)^(infty)((-)1)^k)/(2k+1)
(32)
= 3sum_(k=0)^(infty)（- ）<1)^k
(33)
= 4sum_(k=0)^(infty) (-)です。1)^k
(34)
= sum_(k=0)^(infty)(-)1)^k
(35)
= sum_(k=0)^(infty)(-)1)^k
(36)
= sum_（k=0）^(infty)(-1)^k.
(37)

同様に、piを2^kのべき乗で表すBBP型の公式がいくつか存在する。 4030>

という最初のいくつかの独立式があり、その中で

を参照。

のようになります。

1/(96)sum_(k=0)^(infty)1/(4096^k)

＜170＞ ＜1525＞ =＜3814> =1/(4096)sum_(k=0)^(infty)1/(65536^k)

pi = sum_(k=0)^(infty)1/(16^k)
(38)
= 1/2sum_(k=0)^(infty)1/(16^k)
(39)
= 1/(16)sum_(k=0)^(infty)1/(256^k)
(40)
= 1/(32)sum_(k=0)^(infty)1/(256^k)
(41)
= 1/(32)sum_(k=0)^(infty)1/(4096^k)
(42)
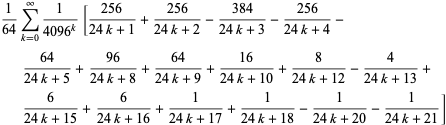= 1/(64)sum_(k=0)^(infty)1/(4096^k)
(43)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(44)
=
(45)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(46)
(47)
= 1/(4096)sum_(k=0)^(infty)1/(65536^k).
(48)

F. Bellardは急速に収束するBBP-typeformula

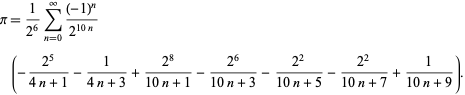pi=1/(2^6)sum_(n=0)^infty((-)) を見つけた。1)^n)/(2^(10n))(-(2^5)/(4n+1)-1/(4n+3)+(2^8)/(10n+1)-(2^6)/(10n+3)-(2^2)/(10n+5)-(2^2)/(10n+7)+1/(10n+9)).
(49)

関連する積分は

pi=(22)/7- となる。int_0^1(x^4(1-x)^4)/(1+x^2)dx
(50)

(Dalzell 1944.JP), 1971; Le Lionnais 1983, p. 22; Borwein, Bailey, and Girgensohn 2004, p.3; Boros and Moll 2004, p.125; Lucas 2005; Borwein et al. 2007, p. 14)です。 この積分は1960年代半ばにK. Mahlerによって知られ、1960年11月のシドニー大学での試験にも登場する（Borwein, Bailey, and Girgensohn, p. 3）。 Beukers (2000)やBoros and Moll (2004, p. 126)は、0と1の積分がpi 333/106となり、333/106が次に収束する有理多項式の自然選択が存在するかどうかは不明である、と述べている。 しかし、第四収束の積分は、

pi=(355)/(113)-1/(3164)int_0^1(x^8(1-x)^8(25+816x^2))/(1+x^2)dx というのが存在します。
(51)

(Lucas 2005; Bailey et al. 2007, p. 219)となる。 実際、Lucas (2005)はこのような積分を他にもいくつか挙げている。

Backhouse (1995)は恒等式

I_(m,n) = int_0^1(x^m(1-)x)^n)/(1+x^2)dx
(52)
= 2^(-(m+n+1))sqrt(π)Gamma(m+1)Gamma(n+1)×_3F_2(1.0),(m+1)/2,(m+2)/2;(m+n+2)/2,(m+n+3)/2;-1)
(53)
= a+bpi+cln2
(54)

正整数mとnで、aのとき。 b、cは有理定数で、piの公式をいくつも生成することができる。 特に2m-n=0 (mod 4)とすると、c=0となる(Lucas 2005)。

同様の式はその後ファーガソンによって発見された。 この2つの式は

pi=sum_(k=0)^infty((4+8r)/(8k+1)-(8r)/(8k+2)-) によって生成できる、この種の式の2次元格子を導くものである。(4r)/(8k+3)-(2+8r)/(8k+4)-(1+2r)/(8k+5)-(1+2r)/(8k+6)+r/(8k+7))(1/(16))^k
（55）

任意の複素値rについて (Adamchik and Wagon)． は、特殊な場合r=0としてBBP式を与えている。

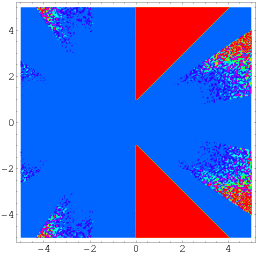
PiFormulasWagonIdentity

Wagonによるさらに一般的な恒等式は

pi+4tan^(-1)z+2ln((1-))2z-z^2)/(z^2+1))=sum_(k=0)^infty1/(16^k)
(56)

(ボーウェインとベイリー 2003, p. 141)のように、実軸に対して対称に配置された2つの三角形の部分を除いた複素平面上の領域で成立する。

同等性のおそらくさらに奇妙な一般クラスは、

pi=4sum_(j=2)^n(2j-1))/4sum_(k=0)^infty1/(16^k) “>

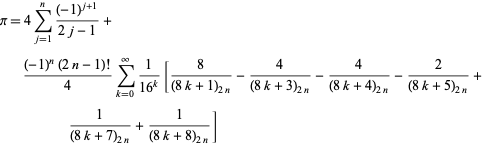pi=4sum_(j=1)^n((-1)^(j+1))/(2j-1)+((-1)^n(2n-1)) で与えられる！ <div><table width=
(57)

これは任意の正の整数 n に対して成り立つが、 (x)_n は Pochhammer symbol (B.Cloitre,pers. comm, 2005年1月23日）。 さらに驚くべきことに、2の自然対数にも酷似した公式がある。

16進数のBBP公式と関連する公式の発見後、他の基底での類似公式が調査された。 Borwein, Bailey, and Girgensohn (2004)は最近、piには2進数でないMachin型BBPアークタンジェント公式がないことを示しているが、これは他の基底における桁抽出アルゴリズムが全く異なる方式であることを否定していない

S.S.。 Plouffeはpiのn番目の桁をO(n^3(logn)^3)ステップで任意の基底で計算するアルゴリズムを考案した。

ラマヌジャン、カタラン、ニュートンによる多数の追加恒等式を、フィボナッチ数の和を含むカステラノス (1988ab, pp. 86-88) によって与えられています。 ラマヌジャンは

sum_(k=0)^infty((-1)^k(4k+1)^3)/(^3)=sum_(k=0)^infty((-)) を発見した。1)^k(4k+1)^3)/(pi^(3/2)^3)=2/pi
(58)

(Hardy 1923, 1924, 1999, p. 7).

Plouffe (2006) は美しい式

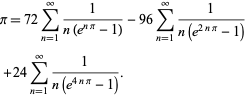pi=72sum_(n=1)^infty1/(n(e^(npi)-1))-96sum_(n=1)^infty1/(n(e^(2npi)-1)) +24sum_(n=1)^infty1/(n(e^(4npi)-1)) を見つけた。
(59)

PiBlatnerProduct

pi とn番目の素数 p_n を関連付けるオイラーによる興味深い無限積公式は

である。

pi = 2/(product_(n=1)^(infty))
(60)
= 2/(product_(n=2)^(infty))
(61)

(Blatner 1997, p.

アルキメデスの方法に似た方法で、n角から始めて、その後の2n角の面積を関連づけることで pi を推定することができる。 βを多角形の1辺の中心からの角度とすると、

β=1/4(n-3)pi となる。
(62)

then

pi=(2sin(2beta))/((n-))/pi(2beta))3)product_(k=0)^(infty)cos(2^(-k)beta))
(63)

(Beckmann 1989, pp. 92-94).

上記の式にn=4をとってpiの正確な式を与えたのはVieta (1593)が最初で、

cosbeta=sinbeta=1/(sqrt(2))=1/2sqrt(2) となります。
(64)

この場合、入れ子式の無限積

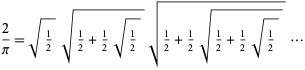2/π=sqrt(1/2)sqrt(1/2+1/2sqrt(1/2))sqrt(1/2+1/2sqrt(1/2))) が発生することになる。..
(65)

(Wells 1986, p. 50; Beckmann 1989, p. 95)となる。 しかし、この式が収束することが厳密に証明されたのは1892年のルディオである。

関連する式は

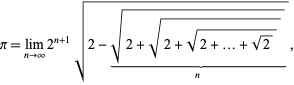pi=lim_(n-infty)2^(n+1)sqrt(2-sqrt(2+sqrt(2+....+sqrt(2)))_()_(n)),
(66)

これは、

pi=lim_(n-infty)2^(n+1)pi_n で書けますね。
(67)

ここでpi_nは反復

pi_n=sqrt((1/2pi_(n-))1))^2+^2)
(68)

with pi_0=sqrt(2) (J. Munkhammar、pers. comm, April 27, 2000)。

pi=2lim_(m-infty)sum_(n=1)^msqrt(^2+1/(m^2)) という式が成り立ちます。
(69)

も密接に関連している。

pi のきれいな公式は

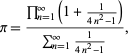pi=(product_(n=1)^(infty)(1+1/(4n^2-1)))/(sum_(n=1)^(infty)1/(4n^2-1))で与えられます。
(70)

ここで分子はπ/2のウォリスの公式の形で、分母は

1/(4n^2-) なので和1/2の伸縮和にする。1)=1/2(1/(2n-1)-1/(2n+1))
(71)

(Sondow 1997)を参照。

Wallisの式の特殊なケースとして

pi/2=product_(n=1)^infty=(2-2)/(1-3)(4-4)/(3-5)(6-6)/(5-7)... がある。
(72)

(Wells 1986, p. 50)となる。 この式は、

lim_(n-infty)(2^(4n))/(n(2n; n)^2)=pilim_(n-infty)(n^2)/(^2)=pi,
(73)

＜1336>ここに、(n; k)は二項係数、Gamma(x)はガンマ関数である(Knopp 1990)。 オイラーは

pi=sqrt(6(1+1/(2^2)+1/(3^2)+1/(4^2)+...) を求めた。)),
(74)

これはリーマンのゼータ関数 zeta(2)=pi^2/6 の特殊値からくるものです。 同様の式は、すべての正の整数 n に対して zeta(2n) から導かれる。

Ramanujan による無限和は

1/pi=sum_(n=0)^infty(2n; n)^3(42n+5)/(2^(12n+4)) である。
(75)

(Borwein et al. 1989; Borwein and Bailey 2003, p.109; Bailey et al.2007, p. 44)。 さらに和はRamanujan (1913-14),

4/pi=sum_(n=0)^infty((-1)^n(1123+21460n)(2n-1)!(4n-1)!)/(882^(2n+1)32^n(n!) に示される。)^3)
(76)

and

1/π = sqrt(8)sum_(n=0)^(infty)(1103+26390n)(2n-1) !!!!!(4n-1)!!)/(99^(4n+2)32^n(n!)^3)
(77)
= (sqrt(8))/(9801)sum_(n=0)^(infty)((4n)!(1103+26390n))/((n!)^4396^(4n))
(78)

(Beeler et al. 1972, Item 139; Borwein et al. 1989; Borwein and Bailey 2003, p. 108; Bailey et al. 2007, p. 44)である。 式(78)は、Borwein and Borwein (1987)よりも前に最初の導出が提示されていないが、次数58のモジュラー恒等式から導出されたものである。 上記の系列はいずれも

pi approx (9801)/(2206sqrt(2))=3.14159273001... を与える。
(79)

(Wells 1986, p. 54) を第一近似として、それぞれ1項あたり小数点以下6桁、8桁程度とする。 このような級数は様々なモジュラー不変量の合理性から存在する。

この級数の一般形は

sum_(n=0)^infty((6n)!)/((3n)!(n!)^3)1/(^n)=(sqrt(-j(t)))/pi,
(80)

ここでtは2次式判別、 j(t) はj関数である。

の場合

b(t) = sqrt(t)
(81)
a(t) = (b(t))/6{1-] のようになります。(E_4(t))/(E_6(t))}。
(82)

そしてE_iはアイゼンシュタイン級数である。 級数p場は定数A=a(t)、B=b(t)、C=c(t)のp次の代数整数を含む。 整数項のみからなる級数のうち、最も短時間で多くの数字を与えるものは、最大の級数1判別式であるd=-163に対応し、Chudnovsky兄弟(1987)によって定式化されたものである。 ここで登場する163は、e^(pisqrt(163))（ラマヌジャン定数）が極めてほぼ整数であることに登場するものと同じである。 同様に640320^3の因子はj(1/2(1+isqrt(163)))のj-function identityからきている。 この級数は

1/pi = 12sum_(n=0)^(infty)((-1)^n(6n)!(13591409+545140134n))/((n!)^3(3n)) から求まる。(640320^3)^(n+1/2))
(83)
= (163·8·27·7·11·19·127)/(640320^(3/2))sum_(n=0)^(infty)((13591409)/(163·2·9·7·11·19·127)+n)((6n)!)/((3n)!(n!)^3)((-1)^n)/(640320^(3n))
(84)

(Borwein and Borwein 1993; Beck and Trott; Bailey et al. 2007, p. 44)である。 この系列は1項あたり14桁を正確に与える。 別の形で同じ式がChudnovsky兄弟(1987)によって与えられ、Wolfram Languageでpiを計算するのに使われている（Vardi 1991; Wolfram Research)、

pi=(426880sqrt(10005))/(A),
(85)

where

A = 13591409
(86)
B = -1/(151931373056000)
(87)
C = (30285563)/(1651969144908540723200).
(88)

クラス番号2（最大判別式-427）の最適式は

1/pi=12sum_(n=0)^infty((-1)^n(6n))!(A+Bn))/((n!)^3(3n)!C^(n+1/2))です。
(89)

where

A = 212175710912sqrt(61)+1657145277365
(90)
B = 13773980892672sqrt(61)+107578229802750
(91)
C = ^3
(92)

(Borwein and Borwein 1993) とあるように、このようになる。 この級数は項が増えるごとに約25桁ずつ増えていく。 クラス番号3の最も収束の早い級数はd=-907に相当し、1項あたり37〜38桁の数字を与える。 クラス番号4の最も早く収束する級数は d=-1555 に相当し、

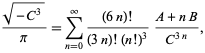(sqrt(-C^3))/pi=sum_(n=0)^infty((6n)!)/((3n)! (n!)^3)(A+nB)/(C^(3n))です。
(93)

where

の場合

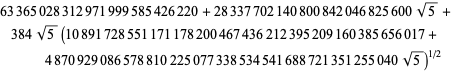A = 63365028312971999585426220+28337702140800842046825600sqrt(5)+384sqrt(5)(10891728551171178200467436212395209160385656017+4870929086578810225077338534541688721351255040sqrt(5))^(1/2)
(94)
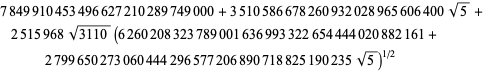B = 7849910453496627210289749000+3510586678260932028965606400sqrt(5)+2515968sqrt(3110)(6260208323789001636993322654444020882161+2799650273060444296577206890718825190235sqrt(5))^(1/2)
(95)
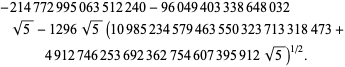C = -214772995063512240-96049403338648032sqrt(5)-1296sqrt(5)(10985234579463550323713318473+4912746253692362754607395912sqrt(5))^(1/2).
(96)

これで1項50桁になる。 Borwein and Borwein (1993)は任意の級数に対してこのような級数を生成する一般的なアルゴリズムを開発した。

Ramanujanの第2、第3ノートに見られる1/piの級数の完全なリストはBerndt (1994, pp.)によって示されている。 352-354)、

となる。

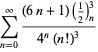4/pi = sum_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!)^3)
(97)
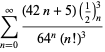(16)/pi = sum_(n=0)^(infty)((42n+5)(1 1/2)_n^3)/(64^n(n!))^3)
(98)
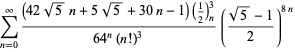(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(99)
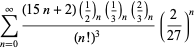(27)/(4pi) = sum_(n=0)^(infty)((15n+2)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(2/(27))^n
(100)
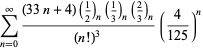(15sqrt(3))/(2pi) = sum_(n=0)^(infty)((33n+4)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(4/(125))^n
(101)
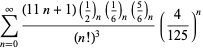(5sqrt(5))/(2pisqrt(3)) = sum_(n=0)^(infty)((11n+1)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(125))^n
(102)
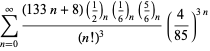(85sqrt(85))/(18pisqrt(3)) = sum_(n=0)^(infty)((133n+8)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(85))^(3n)
(103)
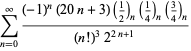4/pi = sum_(n=0)^(infty)((-1)^n(20n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^32^(2n+1))
(104)
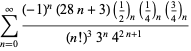4/(pisqrt(3)) = sum_(n=0)^(infty)((-1)^n(28n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^33^n4^(2n+1))
(105)
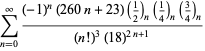4/pi = sum_(n=0)^(infty)((-1)^n(260n+23)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(18)^(2n+1))
(106)
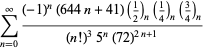4/(pisqrt(5)) = sum_(n=0)^(infty)((-1)^n(644n+41)(1/2)_n(1/4)_n(3/4)_n)/((n!)^35^n(72)^(2n+1))
(107)
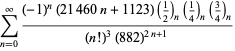4/pi = sum_(n=0)^(infty)((-1)^n(21460n+1123)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(882)^(2n+1))
(108)
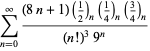(2sqrt(3))/pi = sum_(n=0)^(infty)((8n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^n)
(109)
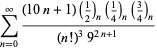1/(2pisqrt(2)) = sum_(n=0)^(infty)((10n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^(2n+1))
(110)
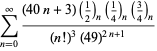1/(3pisqrt(3)) = sum_(n=0)^(infty)((40n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(49)^(2n+1))
(111)
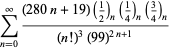2/(pisqrt(11)) = sum_(n=0)^(infty)((280n+19)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(2n+1))
(112)
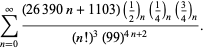1/(2pisqrt(2)) = sum_(n=0)^(infty)((26390n+1103)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(4n+2)).
(113)

これらの方程式はBorwein and Borwein (1987a, pp. 177-187) によって最初に証明された。 Borwein and Borwein (1987b, 1988, 1993) はこのタイプの他の方程式を証明し、Chudnovsky and Chudnovsky (1987) は他の超越定数について同様の方程式を発見した (Bailey et al. 2007, pp. 44-45)。

このタイプの独立した既知の方程式の完全なリストは、

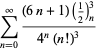4/pi = sum_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!)) によって与えられます。)^3)
(114)
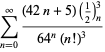(16)/pi = sum_(n=0)^(infty)((42n+5)(1/2)_n^3)/(64^n(n!))^3)
(115)
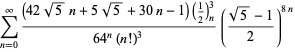(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(116)
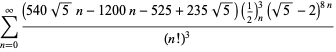(5^(1/4))/pi = sum_(n=0)^(infty)((540sqrt(5)n-))<38181200n-525+235sqrt(5))(1/2)_n^3(sqrt(5)-2)^(8n))/((n!)^3)
(117)
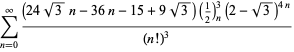(12^(1/4))/pi = sum_(n=0)^(infty)(24sqrt(3)n->()36n-15+9sqrt(3))(1/2)_n^3(2-sqrt(3))^(4n))/((n!)^3)
(118)

for m=1 with nonalternating sign.となります。

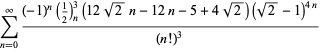2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(12sqrt(2)n-12n-5+4sqrt(2))(sqrt(2)-1)^(4n))/((n!)^3)
(119)
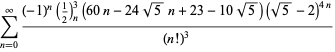2/pi = sum_(n=0)^(infty)((-))/(-)1)^n(1/2)_n^3(60n-24sqrt(5)n+23-10sqrt(5))(sqrt(5)-2)^(4n))/((n!)^3)
(120)
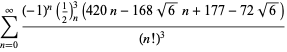2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(420n-168sqrt(6)n+177-72sqrt(6)))/((n!)^3)
(121)
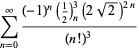(2sqrt(2))/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(2sqrt(2))^(2n))/((n!)^3)
(122)

for m=1 符号を交互に変えています。

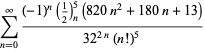(128)/(pi^2) = sum_(n=0)^(infty)((-1)^n(1/2)_n^5(820n^2+180n+13))/(32^(2n)(n!)))^5)
(123)
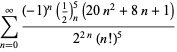(32)/(pi^2) = sum_(n=0)^(infty)((-1)^n(1/2)_n^5(20n^2+8n+1))/(2^(2n)(n!)^5)
(124)

for m=2 (Guillera 2002, 2003, 2006),

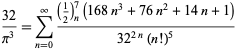(32)/(pi^3)=sum_(n=0)^infty((1/2)_n^7(168n^3+76n^2+14n+1))/(32^(2n)(n!)^5)
(125)

for m=3 (Guillera 2002, 2003, 2006), and no others for m3 has been known (Bailey et al. 2007, pp.45-48）。

Bellard はエキゾチックな式

pi=1/(740025) を出しています。
(126)

where

P(n)=-885673181n^5+3125347237n^4-2942969225n^3+1031962795n^2-196882274n+10996648.
(127)

Gasper は結果

pi=(16)/3^(-1) を引用してますね。
(128)

ここで_1F_2 は一般化超幾何関数で、これを

pi=lim_(x-infty)4x_1F_2(1/2;3/2,3/2;-x^2).
(129)

Gosperによる魅力的な結果は、

lim_(n-infty)product_(i=n)^(2n)pi/(2tan^(-1)i)=4^(1π)=1.554682275 ...によって与えられました。
(130)

pi は不等式

(1+1/π)^(pi+1) 約 3.14097pi を満たしています。
(131)

D. Terr (personal comm.) は、不思議な恒等式

(3,1,4)=(1,5,9)+(2,6,5) (mod 10)
(132)

に言及した、πの最初の9桁に関わること

を指摘した。

コメントを残す

メールアドレスが公開されることはありません。