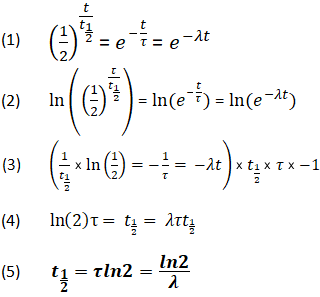以下のツールは、崩壊を受ける物質が半分に減少するための半減期の公式で他の3つの値から任意の1つを生成できます。

Half Life Calculator
4番目の値を算出するには以下のうち任意の3つを提供してください。
半減期、平均寿命、および崩壊定数の変換
残りの2つを得るために、以下のいずれかを提供してください。
定義および式
半減期とは与えられた量がその初期値の半分に減少する時間量と定義されています。 この用語は放射性崩壊を起こす原子に関連して最もよく使われますが、指数関数的かどうかにかかわらず、他のタイプの崩壊を説明するために使用することができます。 半減期の最も有名な応用例は、炭素14の年代測定である。 炭素14の半減期は約5,730年で、約5万年前までの年代を確実に測定することができる。 炭素14年代測定法は、ウィリアム・リビーによって開発されたもので、炭素14が大気中で常に作られていることに基づいている。 光合成によって植物に取り込まれ、さらに動物が植物を食べることで動物にも取り込まれる。 植物や動物が死ぬと炭素14は放射性崩壊し、試料中の炭素14の量を測定することで、その植物や動物がいつ死んだかの情報を伝えることができるのです。
以下に指数関数的減衰を記述する3つの等価式を示す。
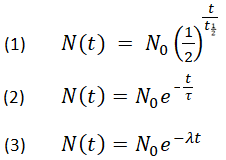
- ここで
N0は初期量
Ntは時間後の残存量、t
t1/2は半減期
τは平均寿命
λは崩壊定数
もしある考古学者が化石サンプルに生きたサンプルと比較して25%炭素14を含むものを見つけたら、次のようになります。 Nt、N0、t1/2がわかっているので、式1を並べ替えることで化石サンプルの死亡時刻を決定できる。
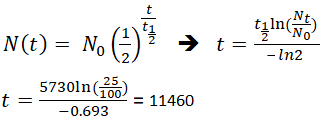
この化石は11,460年前のものである。
半減期定数の関係の導出
上記の式を使って、t1/2、τ、λの関係を導くことも可能で、少なくとも一つの値が分かっていればすべての値を決定することが可能である。