“Men talk of killing time, while time quietly kills them”
Dion Boucicault – London Assurance (1841)
- 今日まで、粒子の運動学と力学を、粒子のシステム（特に剛体）の質量中心の運動から、並進運動や円運動も含め考えてきました。 後者の場合、外からの並進力に関する限り、物体のすべての質量が質量中心に位置すると想像できる。
-
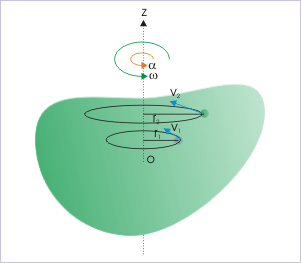次に、固定した回転軸を中心とした剛体の回転を考える。 剛体を考えるので、その中のすべての粒子は他の粒子に対して固定されたままであることに注意されたい。 つまり、このような回転運動では、すべての粒子は回転軸を中心とする円の中を移動することになる。 右の図では、物体はz軸を中心に回転し、2つのサンプル粒子は半径r1、r2の円を描いて移動します。 もし、粒子の半径に直接関係なく、粒子の円運動を記述することができれば、システム内のすべての粒子が同じ方程式で記述されることになります。 粒子の半径は異なっていても、角の回転は同じです。 したがって、角度変数を導入する必要があります。
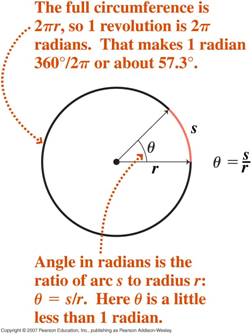
- 角度のラジアン測定
- 角速度（速度）と角加速度
角速度や角加速度は速度や加速度同様の定義がされています。
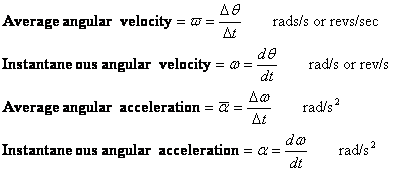
角加速度は求心加速度と同じではありません。 求心加速度は速度の方向の変化によるもので、角加速度は速度の大きさ（回転角を通して）の変化によるものです。
まさに並進の場合と同じように、角速度と角速度の違いは方向です。 角速度には、当該軸を中心とした回転方向が含まれていなければならない。 例えば、x軸を中心に時計回りに10rad/sは角速度、x軸を中心に10rad/sは角速度である。
並進運動方程式との直接的な類推により、一定の角加速度下での単一軸に関する円運動は、以下の4つの方程式により記述され得る。
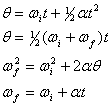
ここで代入すると、
+xが右回りに任意に定義できるように、θの正値は時計回りか反時計回りと定義できることに注意する。
- 角度変数と並進変数の関係
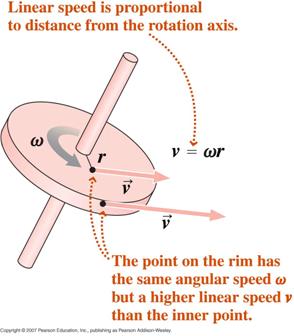ラジアンの定義から、時間に関して微分すると、
vは接線速度とaは接線加速度、と表示されることができる。
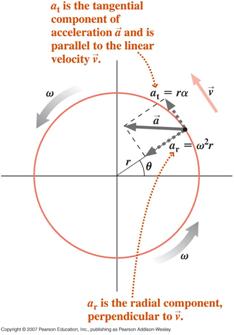
角速度を変えながら円運動をする粒子には、その速度の大きさの変化による接線成分とその速度の方向の変化による径方向（求心）成分という2つの加速度成分が生じます
粒子の純加速度は、以下に示すようにこれら2成分のベクトルの合計となります。
- 参考までに・・・
2軸以上の同時回転は、1次元並進の議論を2次元運動に拡張した発射体運動と同様の方法で考えることができる。 航空機のアプリケーションでは、3軸の回転はRoll、Pitch、Yawとして記述される。
例題
「仕事を通じて不老不死になりたいわけではありません…」。死なないことで達成したい」
Woody Allen – Woody Allen and his Comedy (1975)
ドクター・オブ・ザ・イヤー(Dr. Dr. Dr. Dr. Dr. Dr. Dr. Dr. Dr. Dr. Dr.) C. L. Davis
Physics Department
University of Louisville
email: [email protected]
