はじめに
座標変換は2次元でも十分に非直感的ですが、3次元では非常に苦痛です。 このページでは、以下の順序で取り組んでいます。 (2次元のベクトル、2次元のテンソル、3次元のベクトル、3次元のテンソル、そして最後に4階テンソル変換である。
座標変換の大きな特徴は変換行列の評価で、特に3次元の場合、その評価は重要です。
このページの座標変換はすべて座標系の回転であり、オブジェクト自体は固定されていることを認識することが非常に重要です。 オブジェクト」は力や速度のようなベクトルであったり、部品の応力や歪みのようなテンソルであったりします。 物体の回転については後のセクションで説明します。
ベクトルの2次元座標変換
学術的なポテトは、座標変換がベクトルに適用される方法の優れた例を提供すると同時に、回転するのは座標系であってベクトル…つまりポテトではないことを強調しています。 そこで、右のようにジャガイモに座標系を追加し、ベクトルは “Σ(゚д゚lll) = 2{Cbf i} + 9{Cbf j}” と記述できるようにした。

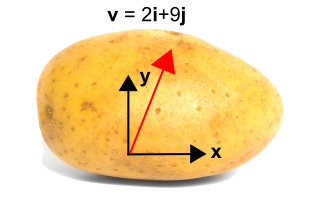
そこで、今度は下の青で示した回転座標系を導入し、using(x’୧), using(y’୧). この座標系は、初期座標系から反時計回りに角度(θ)分回転しています。 ただし、ベクトル自体は全く変わりません。 ベクトル自体は全く変わらない。 しかし、新しい座標系では異なる数値で記述される。 この場合、ベクトルは、”y “軸よりも新しい “x “軸に平行なので、”i “成分は “j “成分よりも大きくなります。
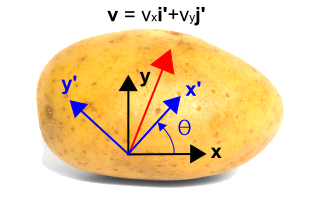
このことから、変換式の4項を構成するのはこの4つの要素であることが分かる。 を設定することで簡単に確認することができます。 황(황theta = 0^╱circ╱)だとすると、╱(v’_x = v_x), 황(v’_y = v_y) となります。 When \(\theta = 90^circui), then \(v’_x = v_yxx) and \(v’_y = -v_x).
Transformation Matrix
変換式は行列を使って書く(扱う)方が便利です。
닫left{ \matrix {v_x} \cos ↵↵↵は行列の対角線上にあり、↵は対角線から外れています。 ただ1つ注意しなければならないのは、マイナス記号が付いてるのがどの \sin \theta Θ の項なのかを覚えておくことです。
The above equation is written in matrix notation as
where \({ễu bf Q}) is the usual letter chosen for the transformation matrix.

Transformation vs Rotation Matrices
もしこの話題がまだ十分に難しくないなら、多くの本やウェブサイトは何が固定で何が回転かを明確にしないことで混乱に拍車をかけています。 このページと次のページでは、オブジェクトが固定されたまま回転しているのは座標系であるため、ここではこれを強調するために変換行列という用語を使用します。 このシナリオでは、オブジェクトが回転していることを強調するために、回転行列という用語が使用されます。
多くの混乱は、各行列 (変換および回転) が他方の行列の転置に過ぎないという驚くべき事実から生じています! したがって、これらは非常によく似ています。 2次元の問題では、実用的な違いは \sin \theta\ の前のマイナス記号が、 \(q_{12}) 項にあるか、 \(q_{21}) 項にあるかということだけです。 (これは3次元変換にも適用される。)変換行列は次のように書くことができる[6855]。
Ⓐ(x’Ⓐ)とⒷ(y)の間の角度は、Ⓐ((90^circ -Ⓐ))、Ⓖ(\cos(x’,y) = (90^circ -Ⓖ)= (\sin Ⓖ)です。
同様に、♪♪♪と♪♪の間の角度は♪♪((90^circ + ♪♪♪theta)♪♪ で、♪♪(♪♪cos( y’,x) = ♪♪cos(90^circ + ♪♪theta) = -♪sin ♪theta ♪)です。
Tensor Notation
座標変換をテンソル記法で書くと
ここで、Ⓐは変換行列Ⓐ({bf Q}Ⓖ)となります。 (行列表記ではなぜ({Θbf Q}) が使われるのかわかりませんが、テンソル表記では \(q_{ij}}) ではなく、 \(\lambda_{ij}}) が使われます)。 \(\lambda_{ij}) は次のように定義されます。
例えば、 \(i = 1), \(j = 2) の場合、
Chi(\lambda_{ij}) はthe \(x’_i) axisとthe \(x_j) axisの角度の方向余弦に相当します。
2-D Coordinate Transforms of Tensors
このセクションでは、テンソル変換の何を、どのように行うかを紹介します。 応力テンソル(δδδ)を基準座標系(x-yδ)から新しい座標系(x’-y’δ)に変換するには、次のようにします。
明示的に行列を書き出すと、
Photo = ⒶⒶⒷ
(ただし応力テンソルは変換しても常に対称になる。)
行列を掛け合わせると
となる。この3つの式はまさに微分要素にかかる力を和して平衡をとった結果の応力テンソルの2次元変換となる。 これはMohrの円でも表現される。
Tensor Notation
座標変換をテンソル表記で書くと
いつものように、テンソル表記はその過程をより深く理解することができる。 今回はラムダの添え字からわかる。 各ラムダは実質的に “the subscript on \(boldsymbol{sigma’}) and one on \(boldsymbol{sigma}})” と対になっています。これはテンソルのランクに関係なく同じです。
3-D Coordinate Transforms of Vectors
2次元の変換で使われる一般式の多くは3次元でも適用可能です。 ベクトルにはz成分があり、変換行列は2×2ではなく3×3です。
6855
3-D Coordinate Transforms of Tensors
今回もルールは変えず、特殊性を持たせた。
行列を明示的に書き出すと
= \leftleft]
このページは3Dのテンソルに対して座標変換を行う。
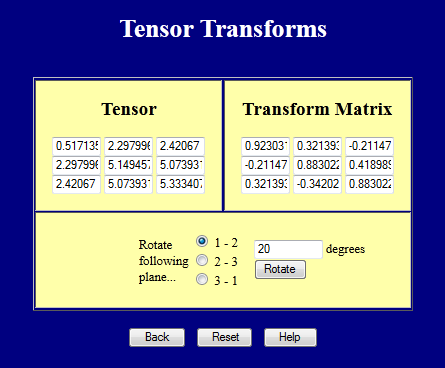
Coordinate Transforms of 4th Rank Tensors
Hookeの法則の項で剛性テンソルは4階、つまり3x3x3x3(4×4ではない)であることがわかる。 ひずみ成分( \epsilon_{kl}) と応力成分( \sigma_{ij}) を関係付けるので、(C_{jkl}) と表記されます。 \4階級剛性テンソルに対する座標変換則はテンソル表記で
と簡単に書けるが、行列表記にするとテンソル方程式で指示されることになる。
まとめ
The coordinate transform of a vector in matrix and tensor notation is
The coordinate transform of a tensor in matrix and tensor notation is
注意: \({}bf Q}) と \(\lambda_{ij}) は同一の変換行列であることに注意してください。
2次元の場合、¥heard({Θbf Q}) と¥heard(Θlambda_{ij}) は以下のように定義されます。