数学テストの幾何学問題対策
一般情報
幾何学は、線と形の勉強の単なる空想上の名前である。 さらに難しい原理やトピックがあることは確かですが、ここでは基本的なことを説明します。 より高度な概念に取り組む前に、これらをマスターする必要があります。
(このガイドで図が「例」と表示されている場合、その図の唯一の表現ではないかもしれませんが、それらの1つであることに注意してください)
点と線
幾何学における点とは、位置であり、その位置が「線」であることを示します。 長さ、幅、深さはない。 点を示すには点と大文字を使う。
線分は2点とその間のすべての点によって定義される。 この2点は線分の端点と呼ばれる。 線分は長さという1つの次元を持つ。 線分を書くには、2つの端点の上にバーを置く。 線を書くには、線の任意の2点に2本の矢印のついたバーを置く。 光線を書くには、右向きの矢印のついた棒を、端点とそれ以外の点 (その方向) の2点の上に置く。 \황(\overrightarrow{AB}) is the ray:

Note: 矢印が左向きのrayは、(황overleftarrow{BA}) とは書けません。 また、順番も重要です。 \황(황overrightarrow{BA})と황(황overrightarrow{AB})は同じではありません。 2602>
2つの線分、セグメント、または光線が直角を形成する場合は垂直です(下記参照)。 垂直であることを表すには、記号(perp)を使用します。 例えば、 \(overline{AB})がperpicular to \(overline{CD})であれば、 \(\overline{AB} \perp) と書くことができます。 
2つの線が交わることがなければ平行である。 もし、(Ⓐ)が(Ⓑ)に平行なら、(Ⓑ)と書くことができます。 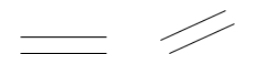
平面図形
幾何学では、平面とは無限に広がる2次元の平らな面をいいます。 2次元とは縦と横のことである。 つまり平面図形は、正方形、円、三角形などの「平らな」図形である。
一般的な図形
多角形は平面上で辺という線分で区切られた閉じた表面である。 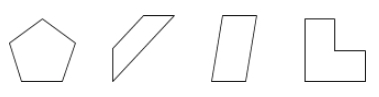
正多角形は、すべての線分と内角が合同である多角形です。
例:
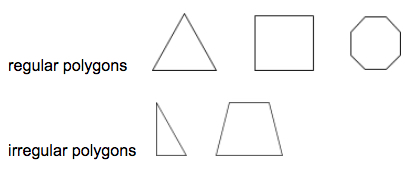
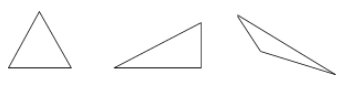
三角形は3辺の多角形です。
例:
四角形-四辺形
平行四辺形は四角形の一種で、向かい合った辺が平行で合同であるものです。 平行四辺形の対角も合同である。 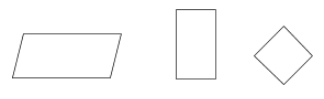
長方形は、4つの直角を持つ平行四辺形です。 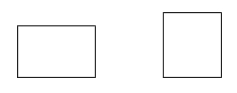
ひし形は、4つの辺がすべて合同である平行四辺形です。 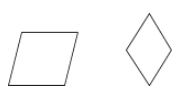
正方形は、ひし形と長方形(すべての辺が合同で、すべての角が直角)を併せ持つ平行四辺形です。 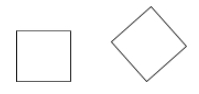
台形は、1組の平行な辺だけを持つ四角形です。
例:: 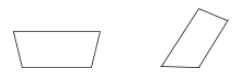
4辺以上の多角形
(^1^) 11辺の多角形は、endecagonまたはundecagonと呼ばれることがあります。 周囲長を求めるには、すべての辺の長さを足せばよい。 正多角形(すべての辺が合同)で、1辺の長さが◇なら、辺の数に◇を掛けて周囲長を求めます。 例えば、正五角形の外周は \(P_text{reg pentagon}=5s)
です。