AC (alternating current) は、電流が2極の間で交互または反転することからこの名前がつきました。 言い換えれば、電流(ひいては電圧)は時間の関数です。 これは、極性が固定され、一般に時間に対して一定である直流電流とは根本的に異なる。 例えば、実験室の直流電圧源は、理想的には端子間の電圧を一定に保ち、時間の経過とともに変化することはない。 これとは対照的に、交流波形は時間の経過とともに前後に揺れ動き、その形状は、正弦波、三角波、方形波などの実験室標準の単純で規則的な経路から、楽器や人間の声が作り出すはるかに複雑でうねる波形まで、幅広い変化を示すことができます
正弦波は、作成できる最も単純な波動です。 時計の秒針の上下変位など、一定速度で回転する単純なベクトルの運動を表す。 図に例を示します。 横軸は時間をプロットしたものです。 左から右に行くほど時間が長くなる(A点がB点の右にある場合、A点はB点より時間的に遅れて発生する)。 縦軸は、ここでは一般的に最大値に対する割合で表していますが、通常は電圧、電流、音圧などの測定値です。
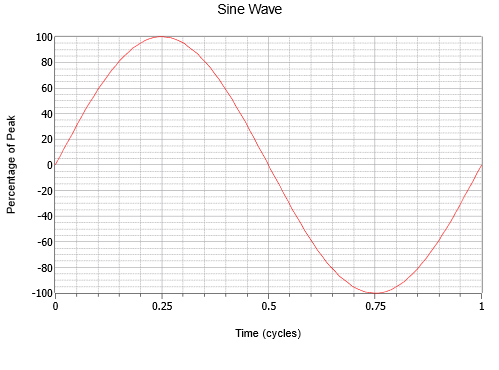
Figure \(\PageIndex{1}): ゼロから始まり、1/4で正のピークに達し、半分でゼロに戻り、3/4で負のピークに達し、再び最初のピークに達するという滑らかな変化に注目してください。 この過程を繰り返す。 この繰り返しを1サイクルと呼びます。 図⑭は、1周期を表しています。正弦波は4分の1波対称です。 つまり、水平軸を中心に反転させたり、ピークを中心に直立させたりすれば、それぞれの4分の1波が同じになるのです。 1周期にかかる時間を周期といい、記号は「(T)」(Time)で表される。 周期の逆数が周波数で、1秒間に何回周回するかを示す。 19世紀のこの分野の研究者の一人に敬意を表して、単位を「cycles per second」と呼ばずに、Heinrich HertzにちなんでHertzと呼び、Hzと略記する。 図には、周波数の異なる3つの正弦波が示されています。最初の波(緑)、周波数の2倍の波(青)、そして周波数の半分または周期の2倍の波(赤)です。 正弦波の周波数の変化です。
波の振幅(縦方向)は、中央のゼロ線から最も正の値までの変化量をピーク量として表すことができます。 また、振幅はpeak-to-peakで表すこともでき、最もマイナスから最もプラスまでの距離を表します。 正弦波の場合、これは常にピーク値の2倍となりますが、非対称な他の波ではそうならないこともあります。 図に振幅の異なる3つの正弦波の系列を示しました。 初期値(緑)の横に、2倍(青)と半分(赤)の振幅のものがある
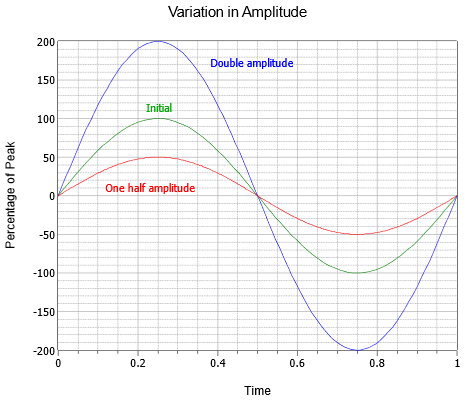
Figure \(\PageIndex{3}): 正弦波の振幅変化
これらのパラメータを組み合わせて、図⑭のような電圧波形を考えてみましょう。 ここでは交流電圧の波形を2周期分見ています。 ピーク値が4V、ピーク・トゥ・ピーク値が8V(一般に「8Vpp」と略される)です。 1周期の周期は0.2秒、つまり”㊙(T = 200㎟) ミリ秒 “です。 また、周波数は “à(f=1/200Ë) “ミリ秒、つまり5Hz(1秒間に5周期)です。
AC波形は、DCオフセットをかけて合成することも可能です。 正のDCレベルを加えると波が垂直に上に移動し、負のDCレベルを加えると波が垂直に下に移動する。 この場合、周波数や振幅のAC部分は変化しない(ただし、絶対的なピークはDC値によってシフトする)。 図にDCオフセットの効果を示します。 最初の波(緑)の上に、元のピーク値の20%に相当する正の直流オフセットを加えた波(青)があります。
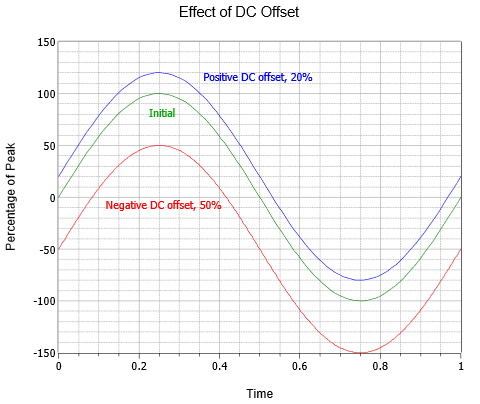
Figure (\PageIndex{5}): 正弦波のDCオフセットの変化
さらに、正弦波は他の正弦波や基準と比較して時間的にずれていることがあります。 このずれを絶対時間として示すことも可能ですが、位相のずれ、つまり、時間を周期の一部分として度数で表すことが一般的です。 例えば、ある正弦が他の正弦より周期の1/4だけ進んでいる場合、leading by 90(^{ Θcirc})(すなわち、360(^{ Θcirc})の1/4)と表現される。 周期の1/2遅れている場合は、180(^{Circ})遅れている(つまり、1/2周期遅れている)と言う。 別の言い方をすると、先行波形は時間的に早く始まるので基準より左に描かれ、遅行波形は時間的に遅く始まるので右に描かれます。
位相シフトの効果を示したのが図( \PageIndex{6}) です。 このプロットでは、(t=0)の値が横軸の中央に移動していることに注意してください。 中央の曲線は初期波(緑)、右の曲線は基準波(緑)である。 左側(赤)は初期波から8分の1周期だけ進んだ波、つまり45(^{Circ}}である。 右側(青)は半分遅れている波で、-22.5(^{Photo_Circ})です。 正弦波の位相変化。
Where
(v(t)ゞ) is the voltage at some time \(t),
(V_{DC}ゞ) is the DC offset, if any,
(V_{P}ゞ) is the peak value,
(fttp) is frequency,
(\thetattp) is the phase shift (+ if leading and drawn to left, – if lagging and drawn to the right).
簡単な例として、図中の波形は振幅が4V(ピーク)、周波数が5Hzで、DCオフセットや位相のずれがない場合です。 したがって、その式は \(v(t) = 4 \sin (2 \pi 5 t)\)
位相シフトを計算するには、まず波形と基準との時間差、ここでは \(Delta t)を決定します。 基準波形は固定点(例えば \(t = 0ờng))でも他の波形でもかまいません。 一般的には、DCオフセットがないと仮定して、ゼロクロスでの差を測定するのが簡単な方法です。 オフセットがある場合は、ゼロクロスがずれた位置(DCオフセットレベル)で測定します。 差がわかったら、その差を周期で割って、シフトを周期の端数で表します。 1周期はベクトルの1回転、つまり360度に相当するので、端数を360度で割れば、位相のずれを度数で表すことができます。 式で表すと、
波が左にシフトしている場合は、先行していて正であり、右にシフトしている場合は、遅れているか時間が遅れているため負であることを忘れないようにします。
例題 \(\PageIndex{1})
図 \(\PageIndex{7}) に示す波形の式を書きなさい。 Waveform for Example \(PageIndex{1}).
この波形は表面的にはFigure \(PageIndex{4}) の波形と似ていますが、騙されないように注意して下さいね。 まず、時間軸が違うのです。 この波形は10ミリ秒で1サイクルが完了します。 したがって、周波数は
第二に、DCオフセットの問題です。 正のピークが4アンペアで発生し、負のピークは-2アンペアで発生することに注意してください。 これは、peak-topeak値が6アンペアであることを示しています。 オフセットがなければ、正のピークは3アンペアとなり、DCオフセットは+1アンペアとなります。 波形の垂直方向の中心は、0アンペアから+1アンペアにシフトアップしています。 この点はt = 0であるため、位相のずれはない。
Example \(\PageIndex{2})
Write the expression for the waveform shown in Figure \(\PageIndex{8}).
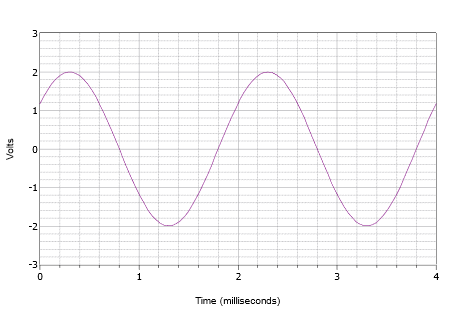
Figure \(\PageIndex{8}).Fill the waves in a figure (Flue)の式は、以下のとおりです。 Waveform for Example \(PageIndex{2}).
まず、正のピークが2V、peak-to-peakの値が4Vとなっていることがわかります。 したがって、DCオフセットはありません。 また、波の垂直方向の中心はⒶから始まらないので、位相のずれがあるはずです。 の値は1.2ボルトです。 波がこの振幅と同じになるのは、▼(t = 2)ミリ秒のときで、もう1サイクル繰り返すようになる。 したがって、周期は2ミリ秒でなければならない。 周波数はこの値の逆数なので、㊙(f = 500㏄)Hzとなります。 2周期目を見ると、1.8ミリ秒でゼロボルトになることがわかります。 従って、0.2ミリ秒のずれがあることになります。 これを度数で表すと、
最終的な式は次のようになります。
まず、-3ボルトのオフセットにより、正のピークが5ボルトから2ボルトに、負のピークが-5ボルトから-8ボルトに押し下げられていることに注意してください。 周波数が40 kHzの場合、周期は次のようになります:
The phase shift of -72}(^{Circ}) represents 72/360, or 0.2 cycles. これは0.2×25(閾値)、つまり5(閾値)の時間遅れに相当します。
最初に、一度に全部を描こうとせず、いくつかのステップを経てプロットを構成すると良い場合があります。 まず、ピーク振幅が5Vで周期が25秒の正弦波を描きます。 次に、正のピークが2ボルト、負のピークが-8ボルトになるように、波形を3ボルト下へ押し下げます。 最後に、新たにシフトした波形を右へ5㌽押し下げます。 その結果が図⑭です。 Waveform for Example \(PageIndex{3}).
1.2.1: 実験室での測定
実験室ではファンクションジェネレーターを使用してサイン波などの波形を発生させることができます。 これらのデバイスは、必要に応じてDCオフセットを加えるとともに、波の振幅と周波数の両方を正確に制御することができる。 図に例を示します。 測定器としては、オシロスコープ、略してスコープがあります。
オシロスコープは、実験室で最も便利で多用途な測定器といえるでしょう。 一般的には、2つまたは4つの入力チャネルを備えていますが、それ以上でも可能です。 各入力チャネルは独自の感度調整を持ち、すべてのチャネルは共通の時間基準を共有する。 ディスプレイには、図のような波形が描かれます。 また、ある電圧と別の電圧のグラフを描くこともできます(X-Yモード)。 最近のオシロスコープには、周波数、振幅、位相シフトなどの自動測定機能やカーソルによる測定機能、表示画像を画像ファイルとして保存できる機能などが追加されています。 4チャンネルのデジタル・オシロスコープの例を図 ㊦に示します。 A digital oscilloscope.
1.2.2: 回路図記号
回路図のうち、交流電圧源と電流源の記号は図(ⅳPageIndex{12} )のとおりです。 極性・方向のマークは絶対的なものではなく、極性・方向が反転する交流電源です。 特に複数の電源が混在する回路では、タイミングを合わせるための目印になります。 2089>
ここで忘れてはならないのは、電源を否定することは、極性を反転させることと同じだということです。 これはDC電源でもそうだったし、AC電源でもそうであることに変わりはない。 このことは、図(ⅳ▿ⅳ)に示されています。 このように、ソースを反転させたり、ネガにしたりすることで、解析が少しわかりやすくなったり、視覚的にわかりやすくなることがあります。 極性・符号の等価性
例題 ㊧図に示すような2つの波がオシロスコープに表示されたとします。 大きい方の25Vの波形(赤)に対する小さい方の20Vの波形(青)の位相のずれを求めます。 まず、どちらの波もDCオフセットがないことに注意してください。 もし、どちらかにオフセットがあるとすれば、ゼロクロスが同じ高さになるように波形を縦にずらす必要があります。 どちらかの波を測定すると、周期は1ミリ秒であることがわかる。 時間的なずれは、ゼロクロスのどの位置でも(4箇所から選択可能)、最も簡単に見つけることができます。 そのずれは0.1ミリ秒と小さく、小さい方の波が大きい方の波より時間的に遅れていることがわかります。 これは負の位相シフトを示します。
Thomas
Thomas
1.2.3: Sines and Cosines
There are a handful of specific phase shifts that are worth to close look at a closer look. 正弦波を反転させると、+180度または-180度シフトした正弦波と見分けがつかなくなります。 つまり、このような波は、3通りの書き方ができるのです。 \つまり、このような波は次の3通りの書き方ができます: \(- \sin (2 \pi ft)\, \(sin (2 \pi ft – 180^{circ})\), or \(\sin (2 \pi ft + 180^{circ})\). また、正弦波を+90度ずらした場合(つまり、先頭から左にずらした場合)には、余弦波と呼ぶこともあります。 よって、♪ \sin (2 \pi ft + 90^{circ}) = ♪ \ cos (2 \pi ft)♪ となります。 最後に、正弦波が-90度ずれる(遅れて右にずれる)場合、負の余弦波または反転した余弦波と呼ばれることがあります。 このように、(Ⓐsin (2Ⓑpi ft – 90^{circ}) = -Ⓑcos (2Ⓑpi ft)Ⓑ) となります。 これら4つの波の関係は、図㊦のようになります。 サインとコサインの時間関係
また、コサイン波がサイン波の1次微分、つまり傾きを表していることも注目すべき点です。 他の学習で思い出したかもしれませんが、直線の傾きまたは「急峻さ」とは、水平方向の変化に対する垂直方向の変化の比率であり、「上昇と下降」と呼ばれることもあります。 電圧の場合は、時間の変化に対する電圧の変化、すなわち「閾値(閾値V/閾値t)」となります。 正弦波のように滑らかで連続的に変化する曲線の場合、ある点での傾きは正しく1次微分として定義され、この場合 \(dv/dt) となります。 そのことを視覚的に確認するために、正弦波の最も急な部分(緑色)は、振幅がゼロと交差するところであることに注意してください。 正の方向に移動しながらゼロを横切るとき(図中のⒶまたはⒷ)、コサイン(青)は正のピークになります。 また、負方向に移動しながら正弦が0を横切るとき(at \(t = 0.5**))、余弦は負のピークを迎えます。 また、正弦波は正のピークと負のピークで傾きが0になり(at \(t = 0.25***), at \(t = 0.75***) )、コサインの振幅も0となる。 また、正弦波は負の余弦波の傾き、負の余弦は負の正弦の傾き、負の正弦は余弦の傾きであることもわかる。 逆に、コサイン波の反微分(不定積分)はサイン波、サイン波の積分は負のコサイン波、などと言うことができます。 これらの関係は、交流回路におけるコンデンサやインダクタの応答に注目したときに、最も役に立つでしょう。 RMS – Root Mean Square Measurement
ピークやピーク・トゥ・ピークとともに、振幅もRMS(Root Mean Square)値として与えられることがあります。 実際、peakまたはpeak-to-peakが指定されない場合、測定はRMSであると見なされます。 RMSは,等価直流電力を求めるための特殊な計算です(オーディオ用パワーアンプなどでは非常に一般的です)。 つまり、抵抗器の電力を求める場合は、電圧や電流のピーク値やピーク・トゥ・ピーク値ではなく、RMS値で計算する必要があります。 そうしないと、誤った電力が発生します。 これは、正弦波、三角波、音楽信号の複雑な波など、波形の種類に関係なく同じことです。 電圧が実効値で指定されている場合、電力計算では同等の大きさの直流電圧と同じように扱うことができる。 例えば、1ボルトのRMS正弦波は、1ボルトのDC電圧と同じ電力散逸と抵抗器への発熱をもたらす。 このため、RMSは実効値(直流実効値)と呼ばれることもあります。
二乗平均平方根という名前は、実効値を決定するプロセスを説明するものです。 まず、電力が電圧または電流の2乗に比例することを思い出してください。 したがって、最初のステップは、入力波形を二乗することになります。 もちろん、波形は時間の関数であり、その2乗によって何らかの新しい形状が得られる。 このとき、この新しい形状の平均値を求める必要がある。 その理由は簡単であるが、必ずしも明らかではない。 電気・電子部品には質量があるため、瞬時に加熱・冷却されることはない。 熱時定数があるのだ。 したがって、時間の経過に伴う平均的な入力に反応する。 ある特定の瞬間の「瞬間ピーク電力」を何らかの方法で計算することは可能だが、それは等価な直流電力を表すものではない。 この二乗波形の平均値を求めたら、対応する直流値はその平均値の平方根に過ぎない。 その結果、0と1の間の分数値が得られ、これがピーク値を実効値化するためのスケーリングファクターとして使用される。 この値は、特定の波形に固有のものとなる。 つまり、すべての正弦波(位相に関係なく)は同じ係数を持ち、すべての正三角形波は同じ係数を持つ、といった具合である。
DC オフセットや位相シフトがなく、振幅が 1 の正弦波の基本式から始めます:
最初のステップは、この波形を二乗することです。 有用な三角恒等式は
これを波に適用すると、
この式は、元の周波数の2倍、元の振幅の半分で、そのピーク値と同じDCオフセットに乗った逆コサイン波を記述しています。 言い換えれば、コサインの負のピークは0に、正のピークは1にあります。次のステップは、この中間結果の平均または平均値を求めることです。 平均値はオフセットの0.5と等しい。 これは、オフセットより上の領域が、オフセットより下の「くぼみ」を完全に埋めているように視覚化することができます。 最後のステップは、平均値の平方根を取ることである。 0.5の平方根は、2の平方根の1倍、つまり約0.707に相当します。 したがって、RMS値はピークの0.707倍となる。 また、ピーク値を2の平方根で割ると、約1.414になります。 この処理を図にすると、図(ⅳ)のようになります。 2089>
まとめると、正弦波の場合、実効値は常にピーク値×0.707になります。 また、任意の正弦波のRMS値は、そのピークを約1.414で割った値であるとも言えます。 この比率は正弦波以外では必ずしも当てはまらない。 その他の一般的な形状の詳細については、付録Cを参照してください。 最後に、ピーク値と実効値の比をクレストレシオと呼ぶ。 これは正弦波では一定の値(やはり約1.414)ですが、オーディオ信号の種類によっては10:1以上になることもあります。 これは大きく変化します。 真空中の光(あるいは近似的に電線中の電流)の場合、速度は毎秒約3E8メートル(すなわち毎秒30万キロ)、あるいは毎秒約18万6000マイルです
速度と周期があれば、波のピークがどのくらい離れているかを想像できます。 この距離を波長といい、ギリシャ文字のλ(ラムダ)で表されます。 波長は速度を周波数で割った値である(˶‾᷄ -̫ ‾᷅˵ )。 したがって、100Hzの正弦波を出すスピーカーの場合、空気中の音速が344m/sなので、( \lambda = 344 m/s ↘ / ↘ 100) Hz、つまり3.44m(11フィート強)である。 周波数が高いほど波長は短くなることがわかります。 また、速度が速いほど波長が長くなることに注意してください。 波長の計算は、電気通信や音響の分野で特に重要である。