How To Think With Exponents And Logarithms

Posted on by admin

指数や対数を含む問題を通して考えるためのトリックを紹介します。 3481>

1) 入力（変化の原因）の話をしているのか、出力（実際に起こった変化）の話をしているのか。

  • 対数は成長を引き起こした入力を明らかにする
  • 指数は成長の最終結果を見つける

2) 成長者の視点、それとも観察者の視点について話しているか。

  • eや自然対数は栽培者の瞬間瞬間の視点
  • 10進法、2進法、など。

頭の中では、選択肢を表にして、

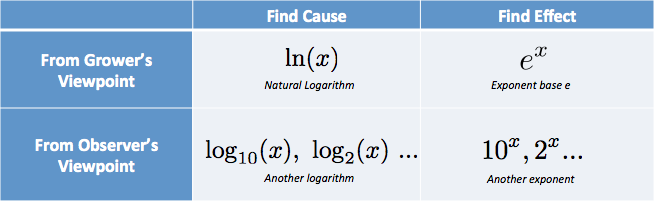
指数対数視点比較

「生産者から見た原因が欲しい…それは自然対数だな」なんて考えているんですけどね。 (自然対数は小文字のLNで略され、高尚なlogarithmus naturalisから)

表の内側、生の関数を説明し、それをいつ使うかを説明するキャプションがない授業にイライラしました！

それでは飛ばない、対数と指数で考える直接練習をしてもらおう

シナリオです。 2000 年から 2010 年にかけて、アメリカの GDP は 9.9 兆から 14.4 兆に変化した

OK、確かに、これらの数字は変化が起こったことを表しています。 しかし、私たちはおそらく、その原因についての洞察を求めています。 この変化を説明する年平均成長率はどのくらいか。

成長からそれを引き起こした率に逆算しているので、私の脳はすぐに「対数」と考えます。 3481>

displaystyle{text{logarithm of change}} のように考えます。 \ЪЪЪ </p> <p>まず、どの対数を使うかですが、私はデフォルトで自然対数を選んでいます。 ほとんどのイベントは、成長する側 (観察者ではない) の観点で終わるので、何が起こっているかを視覚化するために、成長する要素に「一緒に乗る」のが好きなのです。 (</p> <p>次の質問：どのような変化に対して対数を適用するのでしょうか。 これは、同じ期間に9.90ドルから14.40ドルになるのと同じ成長率です。</p> <p><img src=

displaystyle{Threshold(\frac{14.4}{9.9}) = .374}

OK、原因は割合が.374、37.4%でしたね。 これで終わりですか？

まだです。 対数は、変化がどれくらいの時間を要したかについて知りません（私たちは10年と突っ込んでないですよね）。 3481>

変化は確かに37.4%の連続した成長の1年であったり、18.7%の成長の2年であったり、あるいは他の組み合わせであったりするのです。

シナリオから、変化は10年かかったことがわかるので、その率は次のようになるはずです。

displaystyle{ \text{rate} = \frac{.374}{10} = .0374 = 3.74%}

即時連続成長の観点から、米国経済は年3.74%成長したといえる。

この連続率は、成長者の視点であり、あたかも経済が変化していくのに「同乗」しているようなものです。 銀行員が気にするのは、人間にやさしい、前年比の差でしょう。 これは、連続成長を1年間実行させることで把握できます：

displaystyle{text{exponent with rate and time} \ЪЪЪЪ }

\displaystyle{e^{\text{rate} \text{time}} = \text{growth}}

<displaystyle{e^{.0374 \cdot 1} = 1.0381}

前年比は3.8％と、複利による瞬発力3.74％よりもわずかに高い値となっています。 ここで別の言い方をすると、

  • 瞬間的に見ると、経済のある部分が3.74%成長しているのは、$e^(.0374 * years)$
  • 年単位では、複利効果を考慮すると、経済は 3.81% 成長しており、$1.0381^years$

金融では、他のトレンドとうまく比較できる前年比を求める場合があります。 科学や工学では、瞬間的な挙動をモデル化することを好みます。

シナリオ。 自然な成長を記述する

私は、「バクテリアが 24 時間ごとに 2 倍になると仮定し、その成長式を求めよ」といった作為的な例を嫌う。 細菌のコロニーは清潔な人間の間隔で複製され、私たちは正確な倍増を待ち続けるのでしょうか。

より良いシナリオ：「おい、私はいくつかの細菌を見つけて、1 時間待って、塊が 2.3 グラムから 2.32 グラムに成長しました。 今から昼食に行く。 3 時間後に戻ってきたときの量を計算してください」

これをモデル化しましょう。 成長率を求めるには対数が必要で、その成長率を前方に投影するには指数が必要です。 以前と同様に、すべてを自然対数で開始しましょう。

成長因子は次のとおりです。 “>

displaystyle{Centa(\text{growth}) = \ln(2.32/2.3) = .0086 = .86%}

これが1時間のレートで、今後予測する一般モデルは、

displaystyle{text {exponent with rate and time} となります。｝ \ʕ-̫͡-ʔʔ }

displaystyle{e^{.0086 \text{hours}}. \⑭テキスト{成長の影響｝

2.32でスタートして3時間育てると、

displaystyle{2.32 \cdot e^{.0086 \cdot 3} = 2.38}

おっと、菌が2倍になるまでどれぐらいかかりますか？

<displaystyle{1 \cdot e^{.0086 \cdot ⑅} = 2}

両辺の自然対数をとって「指数を元に戻す」ことは機械的にできますが、直観的に考えてみましょう。

2が最終結果だとすると、ln(2)はそこに到達した成長の入力（ある率×時間）です。 レートが0.0086であることが分かっているので、2になるまでの時間は次のようになります。

</displaystyle{ \text{hours} = \frac{{ln(2)}{text{rate}} = \frac{.693}{.0086} = 80.58}

コロニーは〜80時間後に2倍になることが分かっています。 (粘らなくてよかった？)

視点変更の本当の意味

入力 (成長の原因) と出力 (成長の結果) のどちらを求めるかは、非常に簡単です。 しかし、成長者の視点をどのように視覚化するか。

最終的な成長パターンを構築する小さな労働者がいると想像してください (指数に関する記事を参照):

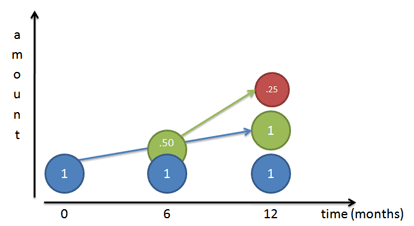
compound interest

成長率が 100% であれば、最初の労働者 (青さん) に対して、着実に働いて 1 年末までに自分の 100% コピーを作成するように指示しているわけです。 3481>

しかし……彼が作っていた労働者（Mr.Green）も働き始める。 6ヶ月の時点でグリーン君が初登場した場合、半年間働くことになり（ブルー君と同じ年率）、レッド君を造ることになります。 もちろん、グリーン氏は6ヶ月しかないので、レッド氏は半分の完成度で終わります。

グリーン氏が4ヶ月後に現れたらどうでしょう。 1ヶ月ですか？ 一日？ 1秒後？ もし労働者がすぐに成長を始めるなら、$e^x$で定義されるinstant-by-instantカーブが得られる：

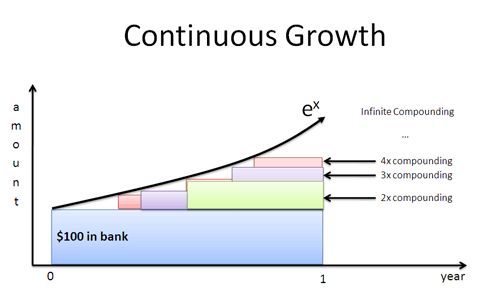
continuous growth

自然対数は、個々の労働者から見た成長速度を与える。 その速度を $e^x$ に突っ込んで、すべての複利計算を含めた最終結果を求めます。

他のベースを使う

他のタイプの対数（10 ベース、2 ベースなど）に切り替えることは、個々の労働者が何をしているかではなく、全体の成長の何らかのパターンを探していることになります。

各対数は、変化を見るときに質問をします：

  • ログベース e:
  • Log base 2：何回の2倍が必要だったか？
  • Log base 10：何回の10倍が必要だったか？

ここで分析するシナリオは、

  • 30年の間に、一般的なチップのトランジスタ数は1000から10億になった

これをどう分析するか。

  • マイクロチップは時間とともにスムーズに成長する単一の存在ではありません。
  • 拡大するマイクロチップに「同乗」しているわけではないので、人間の都合で作られた尺度を使いましょう。 10倍より2倍の方が考えやすい。

これらの仮定で次のようになる：

displaystyle{text{logarithm of change}}. \Ίταμμα για για για για για για για

{{displaystyle}{Dislog_2(\frac{text1 billion}}{1000}) = \log_2(|1 million}) \sim{20 doublings}
「成長要因」は20倍、それが30年かかって分かったのです。 これは、1年に平均2/3倍、つまり1.5年で倍増することになります。

栽培者の視点から計算すると、$lln( \text{1 billion}/1000) / \text{30 years} = 46%$ 連続成長（このシナリオでは少し関係が難しい）です。

私たちの分析を表にまとめることができます。

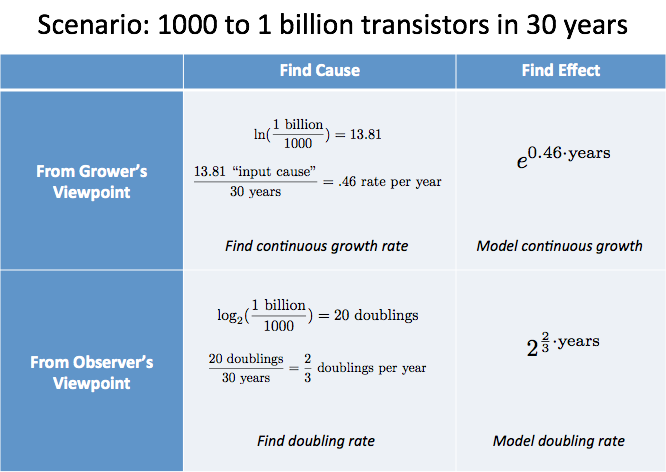
exponents transistor example

まとめ

学習とは、概念の裏にある隠れたキャプションを見つけることである。 それはいつ使われるのか？

私の現在の解釈では、指数は原因 vs. 結果、栽培者 vs. 観察者を問うものだと思います。 しかし、これで終わりではありません。古い概念をどのように再構成できるかを見るのも楽しみの1つです。 The Change Of Base Formula

基底の切り替えについて考える方法を紹介します。 連続成長率を100％とすると、

  • ln(x) は x に成長する時間
  • ln(2) は 2

倍になる時間があるので、x に成長する時間の合計に「合う」数は何個かわかると思うのです。

\displaystyle{text{number of doublings from 1 to x} = \frac{theatln(x)}{theatln(2)} = \log_2(x)}

例えば1～64まで何回倍増するか？

そうすると、ln(64)=4.158です。 そして、ln(2)=0.693です。 3481>

Displaystyle{Thinkfrac{4.158}{.693} = 6}

実世界では計算機の精度が落ちることがあるので、なるべく直積2進数の関数を使うようにしましょう。 もちろん、分数も可能です。 1から2の平方根になるのは「半分」2倍、つまりlog2(1.414)=0.5です。

log base 10に変更すると、10x-ingsの数を数えることになります。

displaystyle{text{number of 10x-ings from 1 to x} = \frac{Gln(x)}{Gln(10)} = \log_{10}(x) }

うまくいきましたよね？ 他の例は「実世界で対数を使う」を読んでください。

このシリーズの他の記事

  1. An Intuitive Guide To Exponential Functions & e
  2. Demystifying the Natural Logarithm (ln)
  3. A Visual Guide to Simple, Compound and Continuous Interest Rates
  4. Common Definitions of e (Colorized)
  5. Understanding Exponents (Why does 0^0 = 1?)
  6. Extrements (指数関数について)
  7. Understanding Exponents (指数関数について))
  8. 実世界で対数を使う
  9. 指数と対数を使った思考法
  10. 離散成長と連続成長を理解する
  11. 指数の本当の意味
  12. Q: なぜeは特別なのですか? (2.718…, 2でも3.7でも他の数でもなく？)

コメントを残す

メールアドレスが公開されることはありません。