比例はシステムの誤差に対応する一つの方法に過ぎません。 比例制御の問題点は、トレンドを検知してそれに合わせて調整することができない点です。 これは積分制御の仕事です。
図6の左側に、システムの誤差の経時変化グラフの例がもう一つあります。 ここでもロボットの物体との距離かもしれないし、タンクの液面かもしれないし、工場のオーブンの温度かもしれない。 ロボットが追いかけている対象は、ロボットが追いつけない速度で遠ざかり続けているのかもしれません。 オーブンのドアシールが磨り減っているかもしれないし、タンクからの液の引き込み量が異常に多いかもしれない。 しかし、プロポーショナルはトレンドに反応するように設計されていないため、問題を発見し修正することができません。 そこで、積分制御が登場します。
積分制御では、誤差値と時間軸の間の領域を測定します。 誤差がゼロに戻らなければ、誤差の面積はどんどん大きくなっていく。 図6の右側は、このような傾向に対して積分出力がどのように反応するかを示している。 誤差曲線と時間軸の間の面積が大きくなると、この面積に比例して出力も大きくなる。 その結果、出力は誤差を修正するためにアクチュエータを強く駆動する。
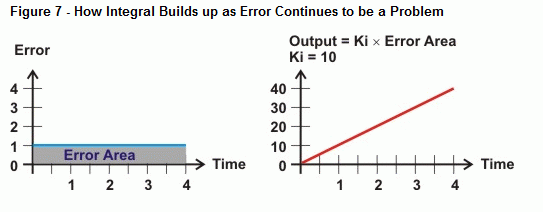
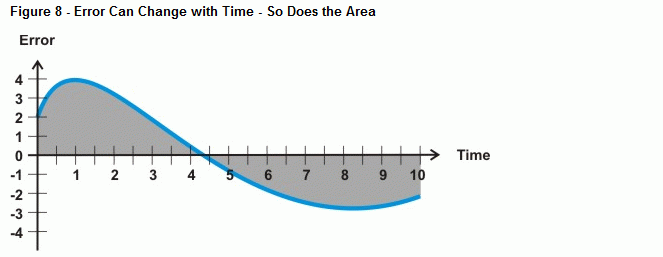
では、誤差が図8に示す曲線のように直線でない場合はどうなるのだろうか。 それは、積分という微積分の演算で、曲線と軸の間の面積を求めるのです。 積分制御の場合、誤差があるまま時間が経過すると、曲線の下の面積が大きくなり、積分計算でシステム誤差に対して駆動するための値も大きくなる。 誤差曲線が時間軸より下に落ちると、負の面積の積み重ねが正の面積の積み重ねから差し引かれる。 正しく調整された場合、積分制御はシステムがゼロの誤差に磨きをかけるのに役立ちます。
BASIC Stampは、数値積分で曲線下の誤差を近似することができます。 図9は、誤差曲線と時間軸の間にある小さな長方形の束の面積を合計することによって、曲線下の誤差を近似する方法を示している。 それぞれの箱の面積は、誤差に測定間の時間を掛けたものです。 すべてのボックスの面積を合計することにより、曲線下の面積の近似値が得られます。 誤差にサンプル間の時間増分を掛けて、次の誤差に時間を掛ける代わりに、各誤差サンプルに時間 1 を掛けるだけでよいのです。 PBASICでこれを行う例を示します。
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
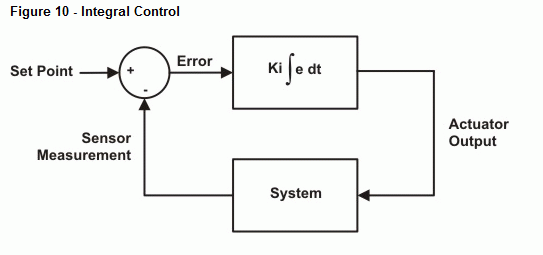
次のサンプルプログラムは、誤差信号の数値積分を行い、それに応じて出力を調整します。 比例制御と同様に、積分出力を目的の値にスケーリングする定数があります。 簡単のために、Kiには再び10を使用することにします。 図10は、制御ループのブロック図である。 Kp ∫ edtとは、Kpに誤差の時間的積分を掛けたものである。
サンプルプログラム – IntegralAlgorithm.bs2
- 入力、保存、実行 IntegralAlgorithm.bs2.
- デバッグターミナルの送信ウィンドウペーンにこの一連の値を入力する。 3 3 3 3 3 3 3 3 3. 3が繰り返されるたびに、積分の出力が大きくなっていることに注目してください。 これがintegralの仕事です。トレンドを検出し、必要に応じて修正するために駆動を大きくします。
- 次に、このシーケンスを試してみてください。 1 2 3 4 5 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0. この曲線の下の面積は、負の面積と正の面積が同じなので、0になります。
' IntegralAlgorithm.bs2' Demonstrates how integral control influences error correction' in a feedback loop. ' {$STAMP BS2}' {$PBASIC 2.5} SetPoint CON 0 ' Set pointKi CON 10 ' Integral constant Current CON 0 ' Array index for current errorAccumulator CON 1 ' Array index for accumulated error sensorInput VAR Word ' Inputerror VAR Word(2) ' Two element error arrayi VAR Word ' Integral termdrive VAR Word ' Output DO DEBUG "Enter sensor input value: " DEBUGIN SDEC sensorInput ' Calculate error. error(Current) = SetPoint - sensorInput ' Calculate integral term. error(Accumulator) = error(Accumulator) + error(Current) i = Ki * error(Accumulator) ' Calculate output. drive = i ' Display values. DEBUG CR, CR, "ERROR", CR, SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR, "INTEGRAL", CR, SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR, "OUTPUT", CR, SDEC ? i, SDEC ? drive, CR, CR LOOP
How IntegralAlgorithm.bs2 Works
このプログラムは ProportionalAlgorithm.bs2 を変更して、代わりに積分計算を行うようにしたものである。 現在、追跡すべき2種類のエラーがあるので、そこでエラー変数配列は2つの要素に拡張されました。 error(0) 変数は現在の誤差を追跡し、error(1) は累積誤差を追跡します。 定数 Current CON 0 と Accumulator CON 1 は error(current) と error(accumulator) で簿記をもう少し賢くします。
作られた他の変更は、誤差が累積されて、積分出力が次の 2 つのステートメントで計算されることです:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
あなたの番-積分出力をクランプ
デバッグターミナルに繰り返し 3 を入力していると分かったかもしれませんが、統合ドライブ出力は本当に暴走し始めるかもしれません。 MIN演算子やMAX演算子を使って、積分制御の出力が暴走しないようにすることができます。 サーボオフセットの動作を繰り返し、出力を650から850に制限してみましょう。
- ドライブ=iステートメントをドライブ=i + オフセットMIN 650 MAX 850に変更します。 2を繰り返し入力し、次に-2を繰り返し入力してみてください。