
数学は非常に重要だが同時に複雑で時間のかかる膨大な数の概念を扱っている。 しかし、Pythonはこの問題を解決するために、本格的なSciPyライブラリを提供しています。 この SciPy チュートリアルでは、いくつかの関数とその例とともに、このライブラリの利用方法を学びます。
先に進む前に、この記事で説明するすべてのトピックを見てください。
それでははじめましょう。 🙂
SciPy はオープンソースの Python ライブラリで、科学や数学の問題を解決するために使用されます。 NumPy 拡張をベースに構築されており、ユーザーはさまざまな高レベル コマンドを使用してデータを操作および視覚化することができます。 前述したように、SciPy は NumPy をベースに構築されているため、SciPy をインポートする場合は NumPy をインポートする必要はありません。
NumPy vs SciPy
NumPy と SciPy はどちらも、数学的および数値解析に使用する Python ライブラリです。 NumPy は配列データとソート、インデックスなどの基本的な操作を含み、SciPy はすべての数値コードで構成されています。 NumPy は線形代数、フーリエ変換などの解決に役立つ多くの関数を提供しますが、SciPy はこれらの関数の全機能バージョンと他の多くの関数を実際に含むライブラリです。 しかし、もしあなたがPythonを使って科学的な分析をしているならば、SciPyはNumPyの上に構築されているので、NumPyとSciPyの両方をインストールする必要があります。
SciPyのサブパッケージ:
SciPyには、以下の表に示すような様々な科学計算のためのサブパッケージがあります:

しかし詳しい説明は、公式文書に従うことができます。
これらのパッケージは、使用する前に排他的にインポートする必要があります。 例えば:
from scipy import cluster
それぞれの関数を詳しく見る前に、まずNumPyとSciPyで共通する関数について見てみましょう。
NumPyとの連携:
SciPyではNumPyをベースにしているので、配列の扱いにはNumPy関数自体を利用することが可能です。 これらの関数について詳しく知るには、help()、info()、source()関数を利用すればよい。
help():
任意の関数についての情報を得るには、help()関数を利用すればよい。
- パラメータなし
- パラメータ使用
ここで、上記の両方の方法を示す例を示します。 2番目のhelp()は、ユーザが情報を求める任意のモジュール、キーワードなどの名前を入力するよう求めます。
info():
この関数は、目的の関数やモジュールなどに関する情報を返します。
scipy.info(cluster)
source():
ソースコードは Python で書かれたオブジェクトに対してのみ返されます。 この関数は、メソッドやオブジェクトがCのような他の言語で書かれている場合、有用な情報を返しません。しかし、この関数を利用したい場合は、以下のようにすることができます。
指数関数と三角関数:
SciPyの特殊関数パッケージは、指数を求めたり三角関数の問題を解いたりできる多くの関数を提供しています。
次の例を考えてみましょう。
EXAMPLE:
from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)
OUTPUT:
1000.0
8.0
1.0
0.7071067811865475
SciPy の特殊関数パッケージには他にも多くの関数があり、自分で試すことができます。
Integration Functions:
SciPyには積分を解くための関数が多数用意されています。 通常の微分積分器から台形規則を使った積分計算まで、SciPy はあらゆる種類の積分問題を解決する関数の宝庫です。
一般的な積分:
SiPy は quad という関数を提供して、1 変数を持つ関数の積分を計算することができます。 限界は無限大を示す ( ) にすることができます。 quad()関数の構文は以下の通りです:
SYNTAX:
quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)
ここで、関数は限界値aとb(無限も可能)の間で積分されることになります。
EXAMPLE:
from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)
上記の例では、関数 ‘a’ は限界値 0, 1 の間で評価されます。 このコードを実行すると、次の出力が表示されます。
OUTPUT:
(3.9086503371292665, 4.3394735994897923e-14)
倍積分関数:
SciPyには倍積分の計算に使用できるdblquadという関数があります。 多くの人が知っているように、二重積分は 2 つの実数変数で構成されます。 dblquad() 関数は積分される関数と、極限と関数 dy と dx を定義する他の 4 つの変数をパラメータとして取ります。333333333335, 1.4802973661668755e-14)
SciPyには他にも三重積分、n積分、Romberg積分などを評価する関数があり、さらに詳しく調べてみることができます。
最適化関数:
scipy.optimizeはよく使われる最適化アルゴリズムを提供しており、ヘルプ機能で確認することができます。
それは基本的に以下のもので構成されています:
- 多変量スカラー関数の無制約および制約付き最小化、すなわち最小化(例: BFGS, Newton Conjugate Gradient, Nelder_mead simplex, etc)
- 全体最適ルーチン (例:Neuton, Newton, Nelder_mead, etc.). differential_evolution、dual_annealing など)
- 最小二乗法および曲線フィット (least_squares, curve_fit など)
- スカラー一変量関数最小化および根探索 (eg…. minimize_scalar and root_scalar)
- Multivariate equation system solvers using algorithms such as hybrid Powell, Levenberg-Marquardt.
Rosenbrook Function:
Rosenbrook function ( rosen) is a test problem used for gradient-based optimization algorithms.This functionはローゼンブルックの関数で、ローゼンブルックは漸化式の最適化アルゴリズムに使用されます。 SciPyでは以下のように定義されています:

EXAMPLE:
import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)
OUTPUT: 7371.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.03999999945
Nelder-Mead:
Nelder-Mead法は、多次元空間における関数の最小・最大値を求めるためによく使われる数値計算法である。 以下の例では、Nelder-Meadアルゴリズムとともにminimize法が使用されている。
EXAMPLE:
from scipy import optimize
a =
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x
OUTPUT: array()
補間関数:
数値分析の分野において、補間とは既知のデータ点のセット内で新しいデータ点を作成することである。 SciPyライブラリにはscipy.interpolateというサブパッケージがあり、スプライン関数とクラス、一次元と多次元(一変量と多変量)補間クラスなどで構成されています。
一変量補間:
一変量補間は基本的には曲線フィットの分野で、一連の二次元データ点に正確にフィットするような曲線を見つけることです。 SciPy は一変量補間を行うために利用できる interp1d 関数を提供しています。
EXAMPLE:
import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()
OUTPUT:
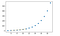
Multivariate Interpolation:
Multivariate interpolation (spatial interpolation )とは2変数から成る機能に対して補間を行うもので、1変数から成る機能に対して補間を行うものです。 次の例は、
interp2d(x, y, z) 関数を使った2次元グリッド上の補間の例を示しています。基本的にx, y, z 配列を使用して、ある関数 interp2d 関数を近似します。 f: “z = f(x, y)” と、その呼び出しメソッドが新しいポイントの値を見つけるためにスプライン補間を使用する関数を返します。
EXAMPLE:
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()
OUTPUT:

Fourier Transform Functions:
Fourier Analysisは関数を周期成分の和として表し、それらの成分から信号を復元する方法を扱ったもので、この関数はFourcing Functionと呼ばれる。 fft 関数は、実数または複素数列の離散フーリエ変換を返すために使用できます。
EXAMPLE:
from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)
OUTPUT.FFT(Fourier Transform Functions):
FFT 関数は、実数または複素数列の離散フーリエ変換を返すために使用できます。
同様に、次のようにifft関数を使用して、この逆数を求めることができます:
EXAMPLE:
rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)
OUTPUT:
信号処理関数:
信号処理は、音、画像などの信号を分析、変更、合成することを扱います。 SciPyには、1次元や2次元のデータを設計、フィルタリング、補間するための関数が用意されています。
フィルタリング:
信号をフィルタリングすることによって、基本的にはその中から不要な成分を取り除きます。 順序付きフィルタリングを行うには、order_filter関数を利用することができます。 この関数は基本的に配列に対して順序付きフィルタリングを実行します。 この関数のシンタックスは次のとおりです:
SYNTAX:
order_filter(a, domain, rank)
a = N 次元入力配列
domain = `a` と同じ次元数を持つマスク配列
rank = ソート後のリストの要素を選択する非負の数(0 が最小で 1 が続く・・・)
EXAMPLE:
from scipy import signal
x = np.arange(35).reshape(7, 5)
domain = np.identity(3)
print(x,end='nn')
print(signal.order_filter(x, domain, 1))
OUTPUT:
]
]
Waveforms:
scipy.signal サブパッケージは、波形を生成するために使用できる様々な関数から構成されています。 そのような関数の1つがchirpです。 この関数は周波数を掃引したコサインジェネレータで、構文は次の通りです:
SYNTAX:
chirp(t, f0, t1, f1, method=’linear’, phi=0, vertex_zero=True)
where,

from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()
OUTPUT.CHIRP(t, f0, t1, f1)
Output:

Linear Algebra:
線形代数では線形方程式とそのベクトル空間や行列を使った表現が扱われます。 SciPy は ATLAS LAPACK および BLAS ライブラリに基づいて構築されており、線形代数に関連する問題を非常に高速に解くことができます。 numpy.linalgのすべての関数に加え、scipy.linalgは他の多くの高度な関数も提供します。 また、もしnumpy.linalgがATLAS LAPACKとBLASのサポートと共に使用されない場合、scipy.linalgはnumpy.linalgより高速です。
行列の逆数を求める:
数学的には、行列Aの逆数は、B=A-1と示される主対角線の下に1で構成されている単位行列がある場合の行列であり、また、B-1と示されている。 SciPyでは、この逆行列はlinalg.invメソッドを使用して得ることができます。
EXAMPLE:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)
OUTPUT:
]
行列式を求める:
行列の係数から演算的に得られる値は正方行列の行列式として知られています。 SciPy では、これは次の構文を持つ関数 det を使用して行うことができます:
SYNTAX:
det(a, overwrite_a=False, check_finite=True)
where,
a : (M, M) 正方行列
overwrite_a( bool, optional) : a のデータの上書きを許可する
check_finite( bool, optional) : a のデータの上書きを許可する。 入力行列が有限個だけで構成されているかどうかをチェックする
EXAMPLE:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)
OUTPUT: -5.0
Sparse Eigenvalues:
Eigenvalues は線形方程式と関連した特定のスカラーセットです。 ARPACKは固有値(固有ベクトル)を非常に高速に求めることができる機能を提供する。 ARPACKの完全な機能は、scipy.sparse.linalg.eigs と scipy.sparse.linalg.eigsh.eigs という二つのハイレベルなインタフェースに収まっています。 eigs インターフェースは実数または複素数の非対称正方行列の固有値を求めることができ、eigsh インターフェースは実対称または複素ヘルミート行列のインターフェースを含んでいます。
eigh関数は複素ヘルミートンまたは実対称行列の一般化固有値問題を解決します。
Complex ndarray :
]
空間データ構造とアルゴリズム:
空間データは基本的に線、点、面などからなるオブジェクトで構成されます。 SciPy の scipy.spatial パッケージは Qhull ライブラリを用いてボロノイ図や三角形分割などを計算することができます。
Delaunay triangulations:
Mathematically, Delaunay triangulations for a set of discrete points in a plane is a triangulation that no point in the given set of points is inside the circumcircle of any triangle.また、平面上の離散点の集合に対する三角形分割も可能です。
EXAMPLE:
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()
OUTPUT:

Multidimensional Image Processing Functions:
画像処理は、情報を取得したり元の画像から拡張した画像を取得するために画像に対して操作を行うことが基本です。 scipy.ndimageパッケージは、任意の次元の配列を扱うように設計された、多数の画像処理および解析関数から構成されています。
コンボリューションと相関。
SciPyには、画像の相関や畳み込みを可能にする関数が多数用意されています。
- 関数 correlate1d は与えられた軸に沿った一次元の相関を計算するために使われます。指定された軸にそって多次元の畳み込み
- The function convolve allows multidimensional convolution of any given array with specified kernel
EXAMPLE:
import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)
OUTPUT: array()
ファイル IO:
The scipy.ioパッケージは、MATLABファイル、IDLファイル、Matrix Marketファイルなど、異なるフォーマットのファイルを管理するのに役立つ多くの関数を提供します。
このパッケージを利用するには、以下のようにインポートする必要があります。
import scipy.io as sio
サブパッケージに関する詳しい情報は、ファイルIOに関する公式ドキュメントを参照してください。 すべてを明確に理解していただけたと思います。
人工知能、DevOps、エシカルハッキングなど、市場で最も人気のある技術に関する他の記事をチェックしたい場合は、Edureka の公式サイトを参照してください。 Python による機械学習分類器
2. Python Scikit-Learn Cheat Sheet
3. 機械学習ツール
4. データ科学および機械学習用の Python ライブラリ
5. Pythonでチャットボット
6. Pythonコレクション
7. Pythonモジュール
8. Python開発者のスキル
9. OOPs インタビューの質問と回答
10. Python開発者のための履歴書
11. Pythonで探索的データ解析
12. PythonのTurtleモジュールでスネークゲーム
13. Python開発者の給与
14. 主成分分析
15. Python vs C++
16. Scrapy チュートリアル
17. Python による Web Scraping
18. 最小二乗回帰法
19. Jupyter Notebook Cheat Sheet
20. Pythonの基本
21. Pythonのパターンプログラム
22. Pythonのジェネレータ
23. Pythonのデコレーター
24. Python Spyder IDE
25. PythonでKivyを使用したモバイルアプリケーション
26. トップ10ベスト書籍は、&練習Pythonの
を学ぶために>
27. Pythonでロボットフレームワーク
28. PyGameを使ったPythonのスネークゲーム
29. Djangoのインタビューの質問と回答
30. Pythonアプリケーショントップ10
31. Pythonのハッシュテーブルとハッシュマップ
32. Python 3.8
33. サポートベクターマシン
34. Python チュートリアル